SLC S23 Semana 6 || Geometría con GeoGebra: Más sobre triángulos, cuadriláteros y círculos

_F

Tarea 1: Construye un triángulo arbitrario, en el que los tres vértices sean móviles. Para este triángulo, construye sus tres excírculos. Demuestra cómo se comportan. Bonificación por construir además la circunferencia interior y la circunferencia exterior.

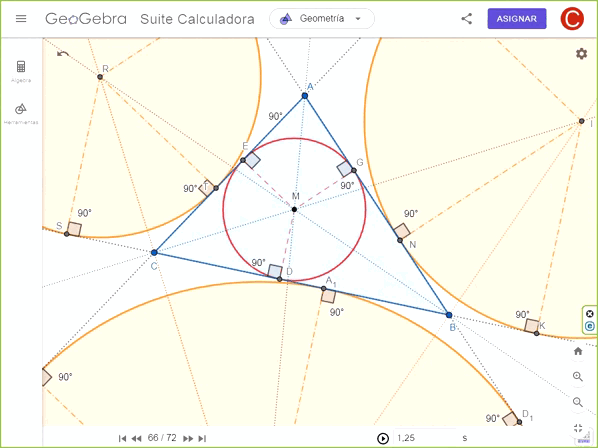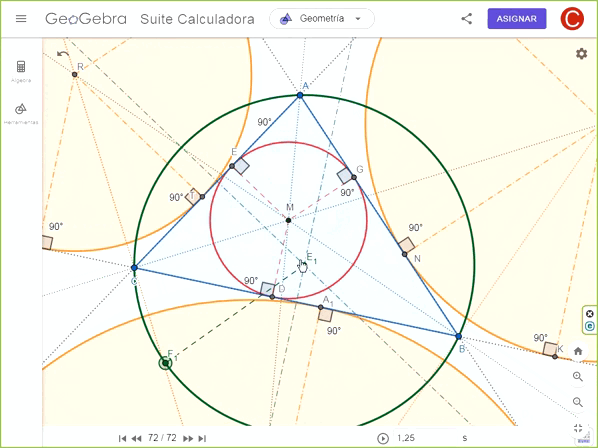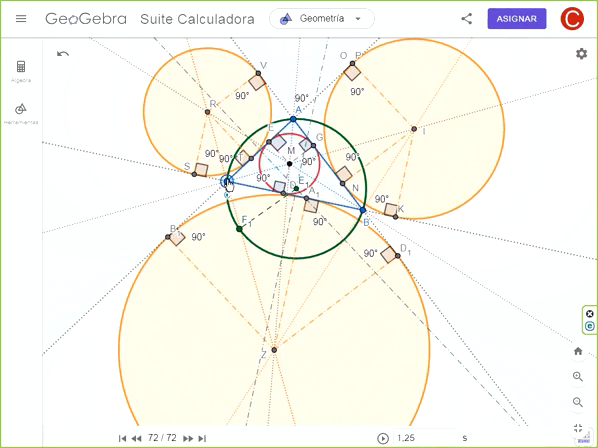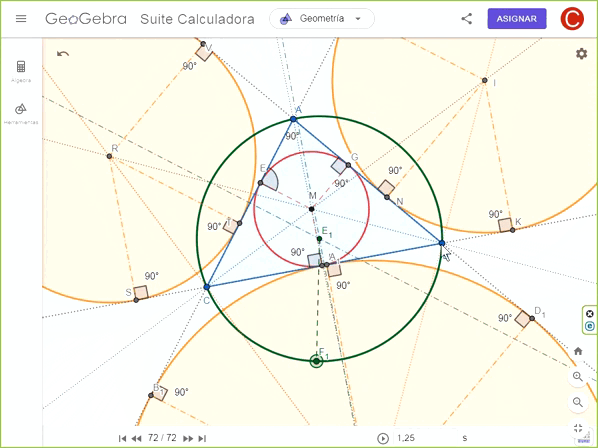
_{Proceso de construcción del triángulo arbitrario, círculo inscrito y excírculos.}
Utilicé la herramienta polígono para trazar un triángulo arbitrario con los vértices ABC y determiné la bisectriz de dos de sus lados para intersectarlas y obtener el centro M del círculo inscrito. Tracé desde dicho centro una recta perpendicular a cada lado del triángulo hallando los puntos de intersección D, E y G, que son los puntos tangentes de la circunferencia inscrita a construir.

Tracé la circunferencia con el centro y cualquiera de estos tres puntos tangentes, como se muestra en el vídeo. Así mismo tracé con un segmento de recta el radio de la circunferencia inscrita para cada lado del triángulo así como sus ángulos rectos que demuestran su perpendicularidad con cada lado del triángulo.

Para construir el primer excírculo, tracé anticipadamente una recta que une dos vértices del triángulo en dos de sus lados a fin de proyectar las tangentes del círculo a crear. Igualmente tracé la bisectriz del ángulo adyacente que se forma entre la línea tangente y el lado del triángulo. En nuestro caso, escogí el vértice B para trazar dicha bisectriz e intersectarla con la bisectriz del vértice C del triángulo.

El resultado de dicha intersección, punto I, es el excentro del nuevo círculo. Por tanto, tracé una línea perpendicular a la tangente por dicho centro para obtener el punto tangente K del nuevo círculo. Análogamente se obtuvieron los puntos tangentes N y y O, con los cuales podemos definir el primer excírculo con centro en I, alineado con el centro M de la circunferencia inscrita a través de su línea bisectriz, tangente al lado AB del triángulo y a las proyecciones externas de sus otros dos lados.

Para proseguir con el segundo y tercer círculo, se realiza la misma tarea con la intersección de las bisectrices del triángulo y del nuevo círculo para obtener los excentros, R y Z. Note que en este último confluyen todas las bisectrices del triángulo y excírculos.

Luego de construir los tres círculos se marcaron los ángulos rectos en los radios correspondientes para demostrar la perpendicularidad y/o tangencialidad.

_{Construcción del círculo circunscrito en el triángulo.}
De las tareas de las semanas anteriores aprendimos que el centro del círculo circunscrito (circuncentro) se obtiene por la intersección de las mediatrices del triángulo contenido. En esta oportunidad utilicé dos mediatrices para ubicar el circuncentro E₁. A partir de este centro tracé el circulo pasando por alguno de los vértices del triángulo ABC.

Coloqué un punto F₁ en esta circunferencia para colocar un radio con un segmento de recta.

En el video Gif se puede observar el movimiento y el efecto que tiene el triángulo ABC con todos los elementos incorporados, notando claramente la conservación de las perpendicularidades, alienación de centros y tangencialidad de los círculos externos con dicho triángulo

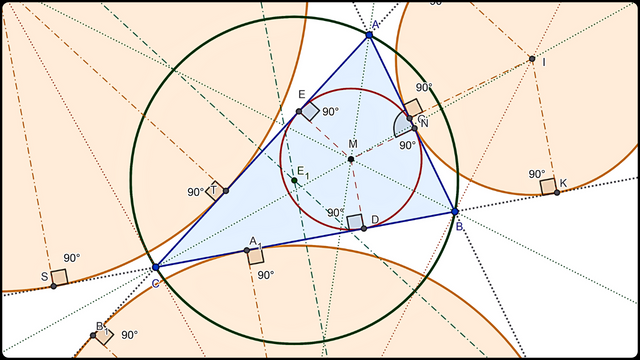_{Resultado del círculo circunscrito en el triángulo.}

Tarea 2: Construye el círculo de Euler ilustrado con todas sus características.

_{Proceso de construcción del círculo de Euler}
Construí un triángulo arbitrario ABC y tracé las tres mediatrices D, E y F. Luego tracé las alturas por cada vértice del triángulo para determinar las bases de cada altura H, I y G respectivamente. Marqué el punto de intersección de las alturas J y el de las mediatrices K.

Tracé el círculo de Euler por tres puntos conocidos que le pertenecen, por ejemplo D, I y E, convalidando el trazado de este círculo que pasa por los puntos H, G y F. También Euler pasa por tres puntos adicionales como M, R y P que se encuentran en la intersección del círculo con las alturas.

Otra de las características del círculo de Euler es que estos puntos M, R y P se encuentran en la mitad de la altura entre el vértice correspondiente del triángulo y el punto J donde se intersectan las alturas. Se identifican en la imagen con colores y estilos diferentes.

Finalmente otra característica del círculo de Euler es que el tamaño de su radio es la mitad del tamaño del radio del círculo circunscrito. Para ello tracé el círculo circunscrito con centro en K y un punto en cualquiera de los vértices A,B o C. Ubiqué un punto L en el círculo para dibujar el tamaño del radio con el segmento KL.

Para hallar el centro del círculo de Euler, le tracé una línea secante y proyecté otra perpendicular por su punto medio para intersectar el círculo y determinar su diámetro. Oculté lo necesario para mostrar solo el centro hallado V como en la imagen. Dibujé su radio con el segmento de recta VW, confirmando que su tamaño es exactamente la mitad de tamaño del círculo circunscrito.

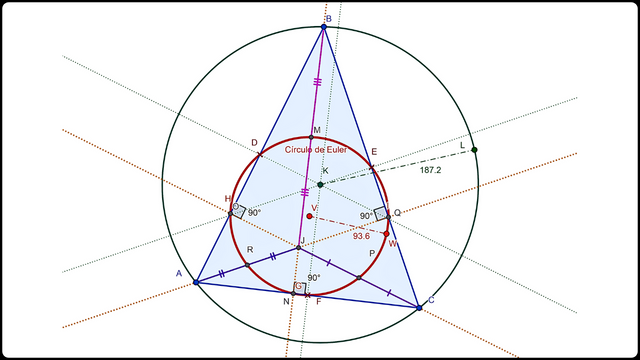_{Círculo de Euler}

Tarea 3: Además de la circunferencia de Euler, también existe la recta de Euler, así como otras circunferencias como la circunferencia de Spieker, la circunferencia de Taylor, la circunferencia de Nagel, la circunferencia de Apollonius, la circunferencia de Malfatti y la circunferencia de Feuerbach. Construye uno de los círculos que he enumerado, o si encuentras otro círculo relacionado con un triángulo.

_{Proceso de construcción del Círculo de Taylor}
Decidí realizar el Círculo de Taylor relacionado a un triángulo. Definí un triángulo arbitrario ABC y tracé sus bisectrices, identificando sus puntos de intersección con cada lado correspondiente del triángulo como D, E y F.

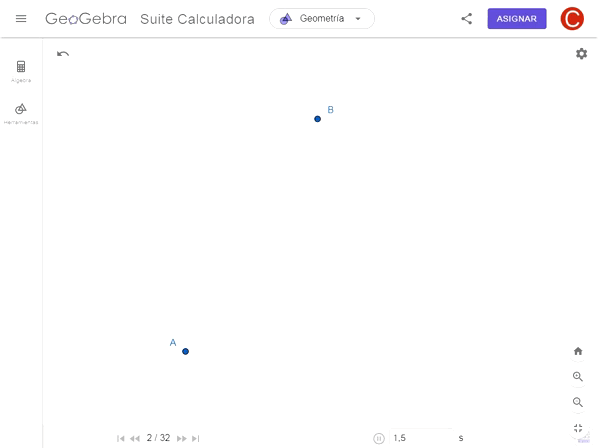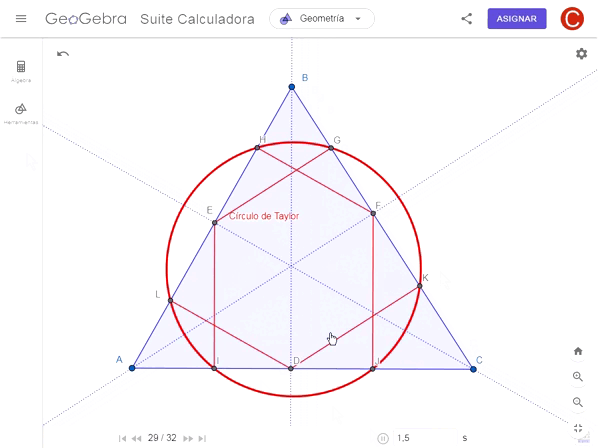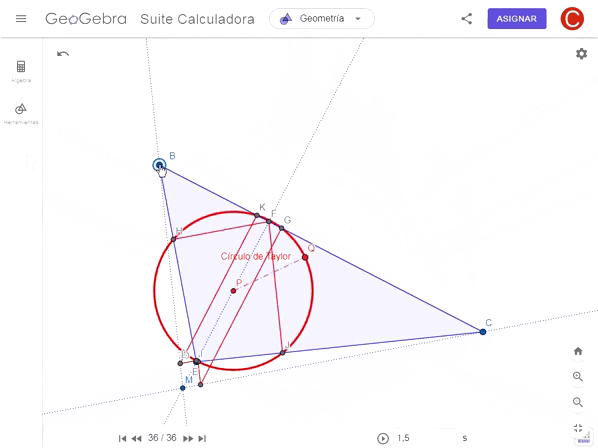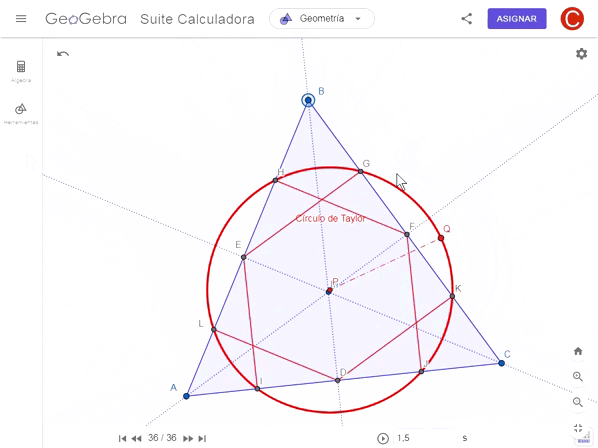
Luego por cada uno de estos puntos tracé una línea paralela a la bisectriz de los otros dos lados, hallando los puntos de intersección con los lados del triángulo identificándolos como F, G, H, I, J, K y L.

El Círculo de Taylor pasa por todos estos nuevos puntos, así que fácilmente con tres de estos puntos se pueden trazar dicho círculo. Es parecido al círculo de Euler solo que pasa por 6 puntos del triángulo en lugar de 9, salvando otras características.

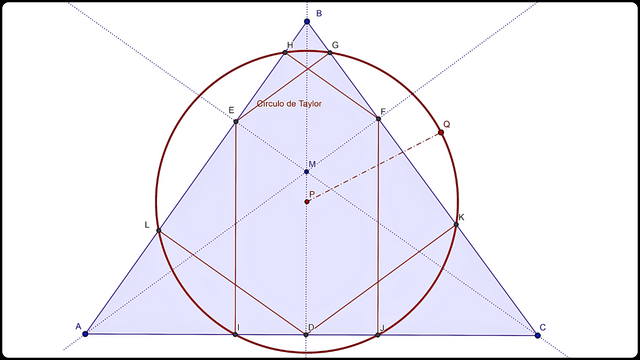_{Círculo de Taylor}

Tarea 4: Construye un cuadrilátero y circunscribe un círculo a su alrededor. El centro del círculo circunscrito (como en un triángulo) se encuentra en la intersección de las bisectrices perpendiculares.

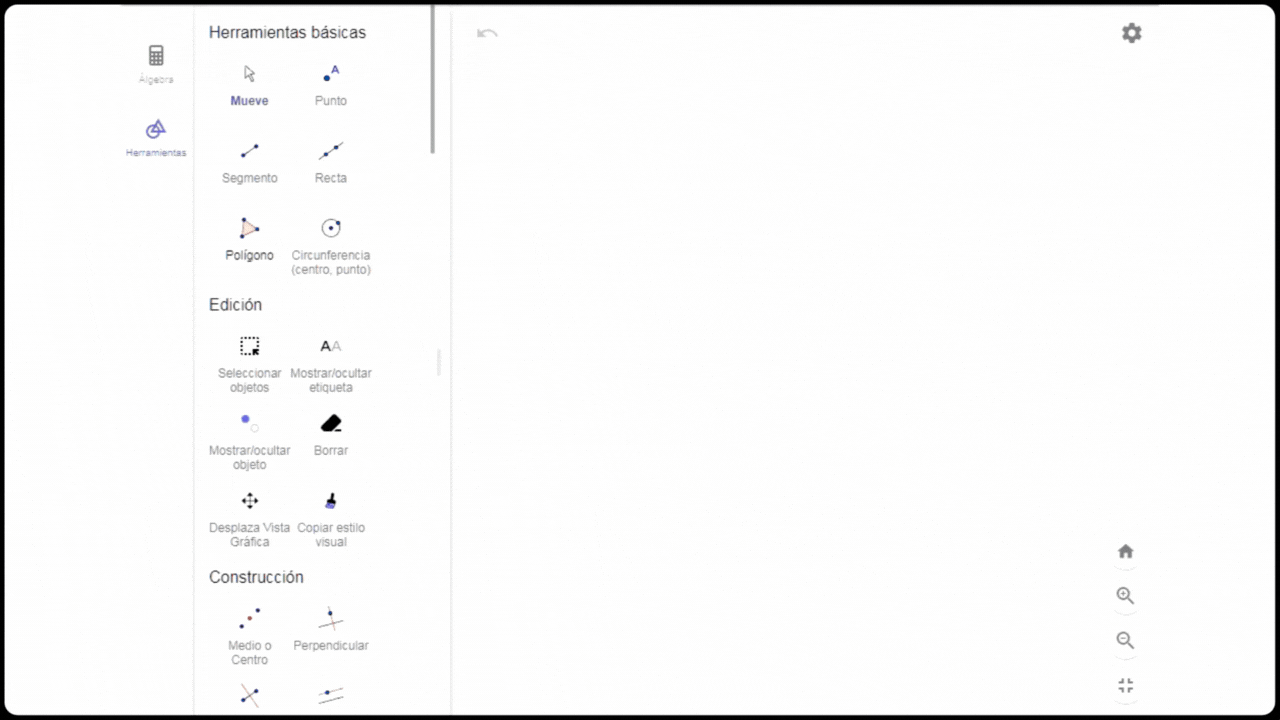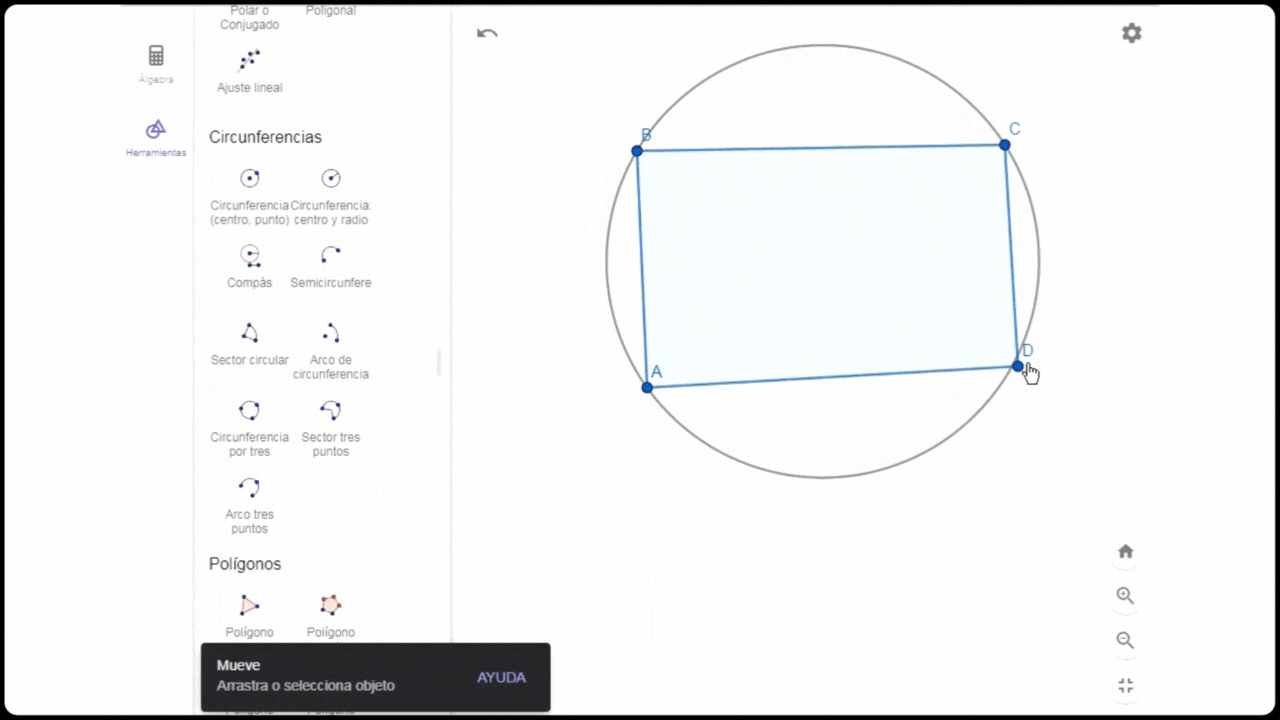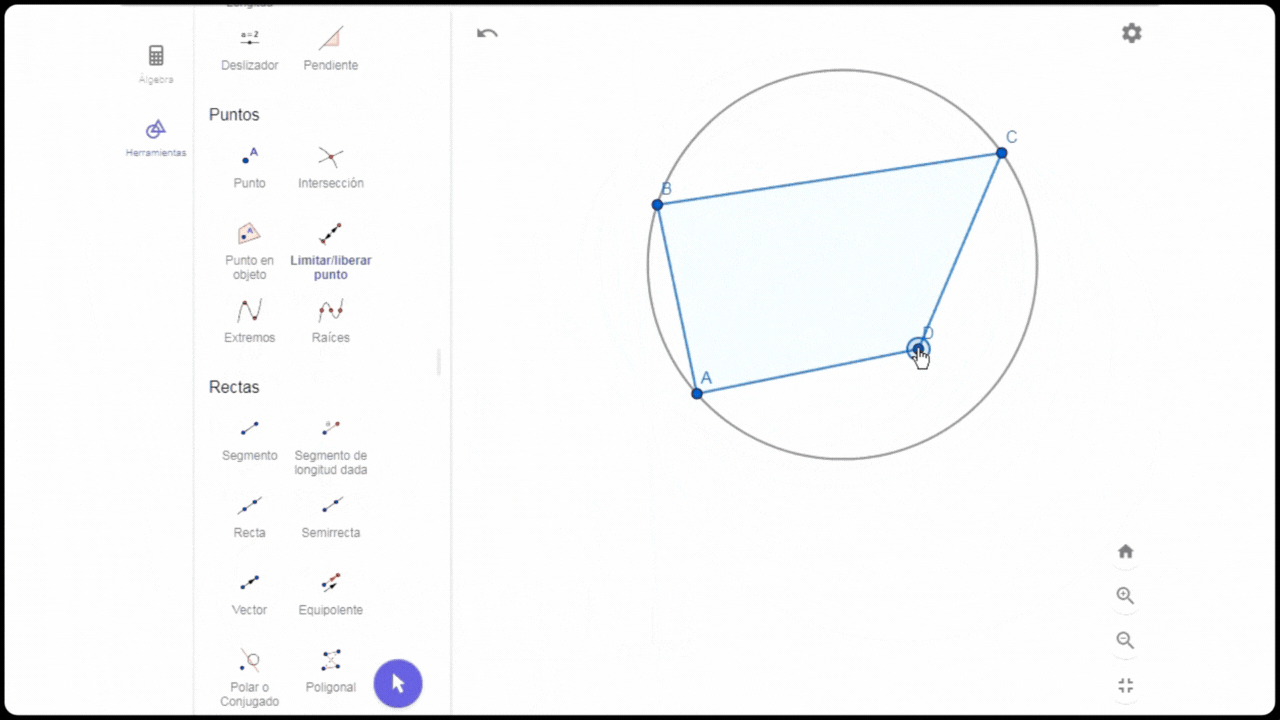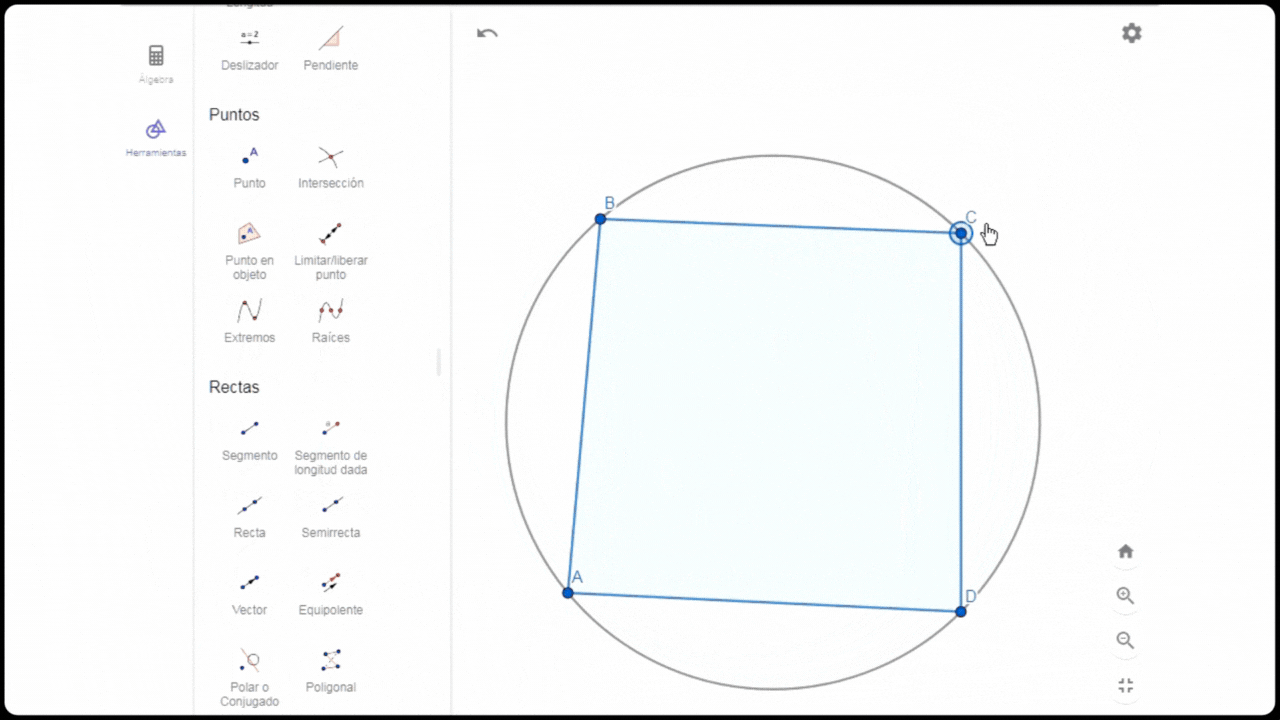_{Construcción de círculo circunscrito en cuadrilátero}
Construí un cuadrilátero arbitrario ABCD y tracé una circunferencia por tres puntos A,B y C. Noté que el punto D quedó fuera de éste, por tanto para incorporarlo utilicé la herramienta limitar/liberar punto. De esta manera ya tengo el cuadrilátero con su circunferencia circunscrita.

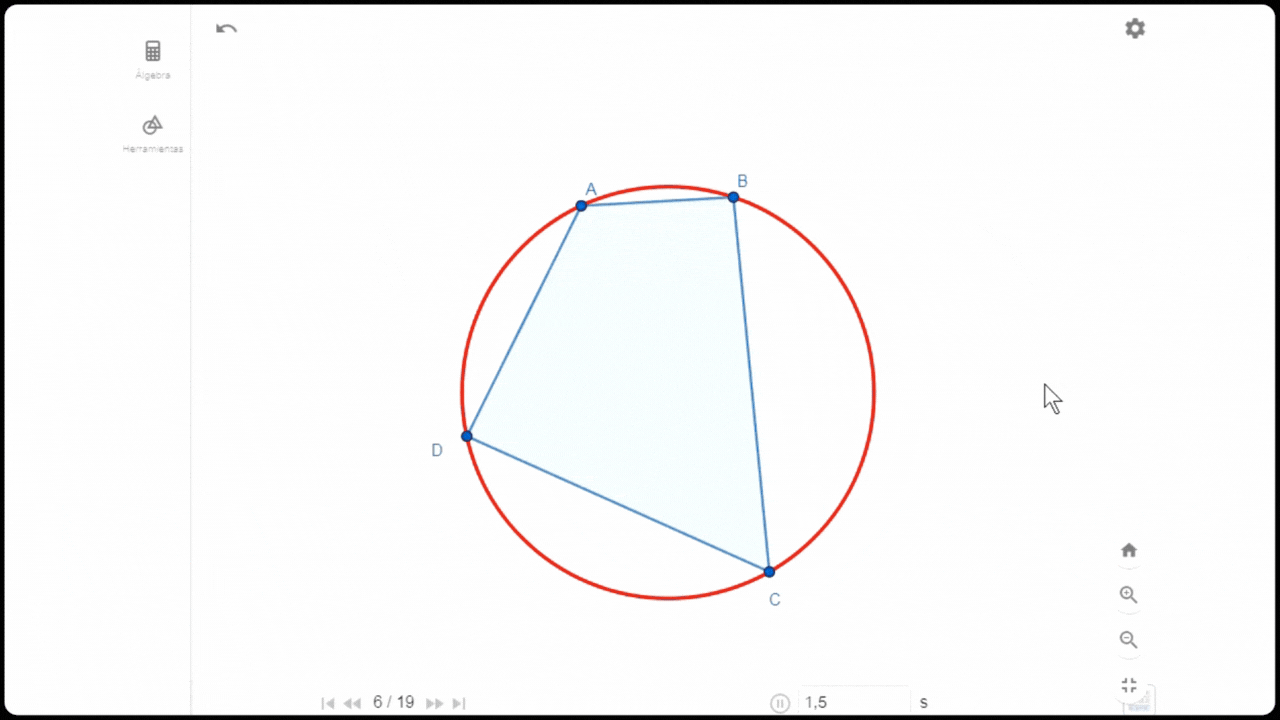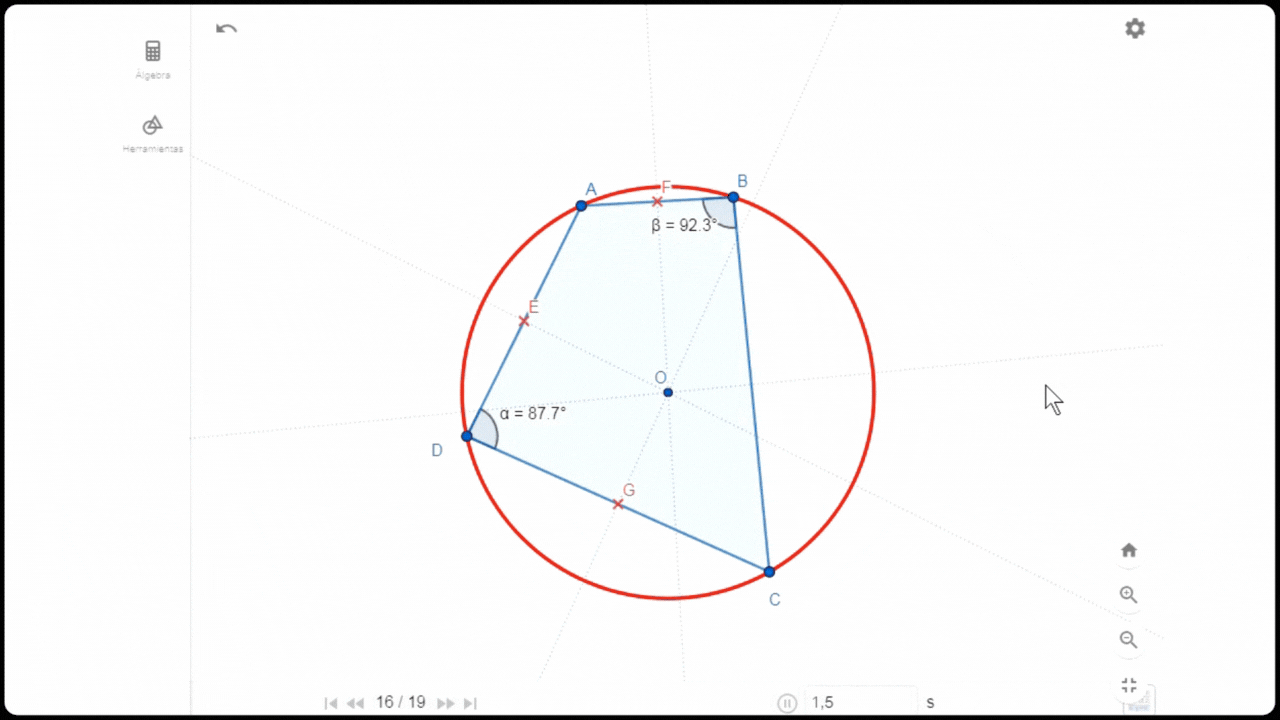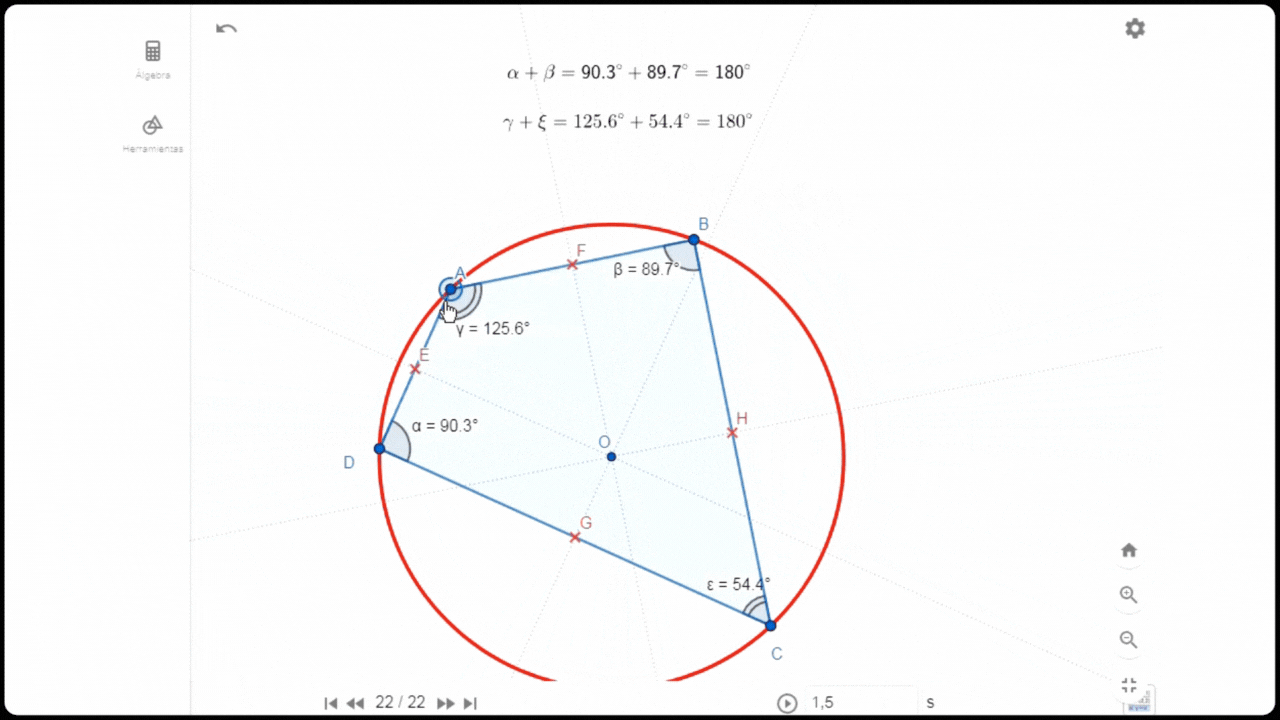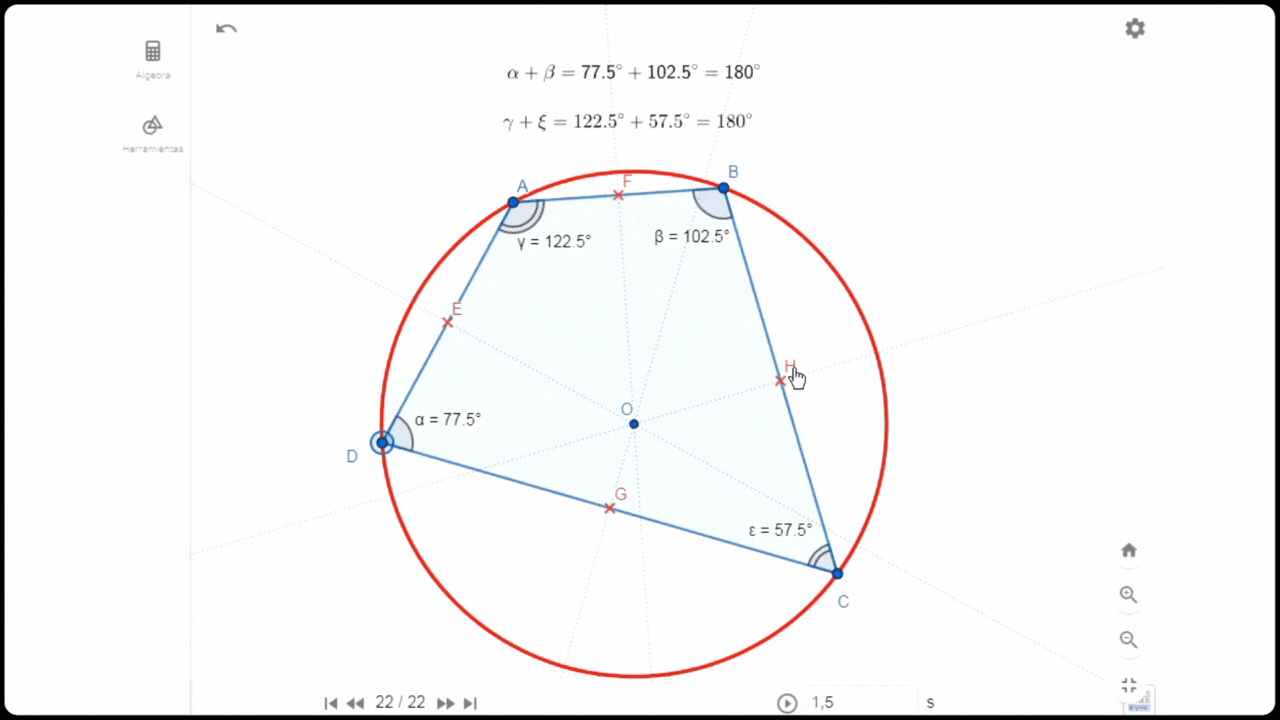_{Características del cuadrilátero que con su círculo circunscrito}
Una de las características de este tipo de cuadrilátero es que la suma de ángulos internos de los vértices opuestos es 180°. Efectivamente ésta se cumple cuando medí dichos ángulos. Para medir otros aspectos, tracé las mediatrices E, F, H y G para obtener el punto de intersección O que pasa a ser el centro de la circunferencia circunscrita del cuadrilátero.

Incorporé todos los ángulos y la expresión algebraica que demuestra la suma de los ángulos de los vértices opuestos.

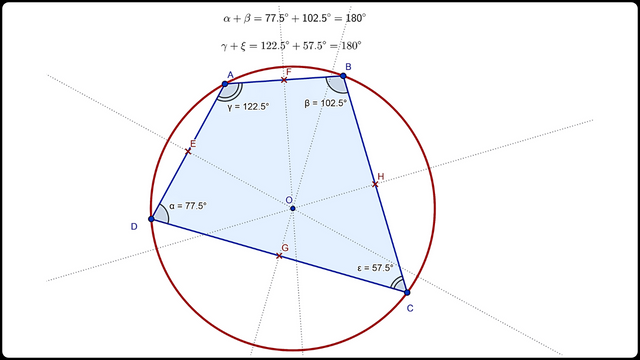_{Círculo circunscrito en cuadrilátero}

Tarea 5: Ilustra un cuadrilátero con una circunferencia inscrita (un dibujo).

_{Círculo inscrito en cuadrilátero}
Coloqué el vértice A del cuadrilátero por el cual salen dos tangentes de una circunferencia a construir. En cada tangente agregué un punto para poder trazar una bisectriz entre las dos líneas tangente y que pasan por el vértice A. A partir de un punto E en la línea tangente tracé una línea perpendicular que intersecta a la bisectriz en el punto D, que representa el centro de la circunferencia. Igualmente por este centro tracé una perpendicular a la otra línea intersectando el punto B.

De tal manera que, teniendo un centro y dos puntos tangentes de la circunferencia, son suficientes para trazar un círculo. Para completar el cuadrilátero se necesitan cuatro tangentes y cuatro vértices, por lo que tracé dos nuevas líneas tangentes a la circunferencia por el punto G e I que al intersectarlas con las otras líneas tangentes generan los tres vértices faltantes ( J, K y L) como se muestra en la imagen.

Se demuestra que la longitud de los lados opuestos del cuadrilátero suman lo mismo que los otros dos lados restantes, siendo una característica geométrica indispensable para que la circunferencia pueda se circunscrita al cuadrilátero ABJKL.

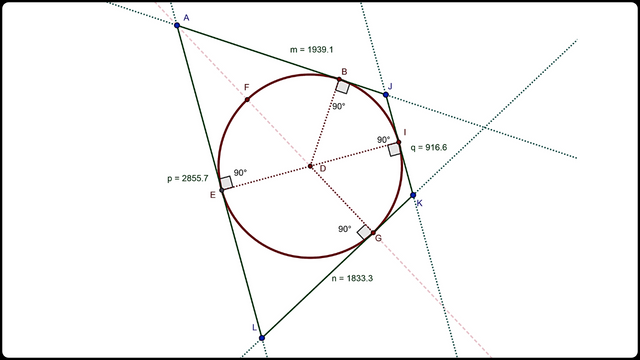_{Círculo inscrito en cuadrilátero}
En este capture se comprueba que la suma de los lados opuestos AL+JK = 2855.70+916.60 = 3772.30 y los lados restantes AJ+LK = 1939.10+1833.3 = 3772.40, son prácticamente iguales con una pequeña diferencia decimal en la precisión de pantalla.

Tarea 6: Representa una cometa y otro cuadrilátero con diagonales perpendiculares (no un rombo ni una cometa) como una animación, no sólo una imagen.

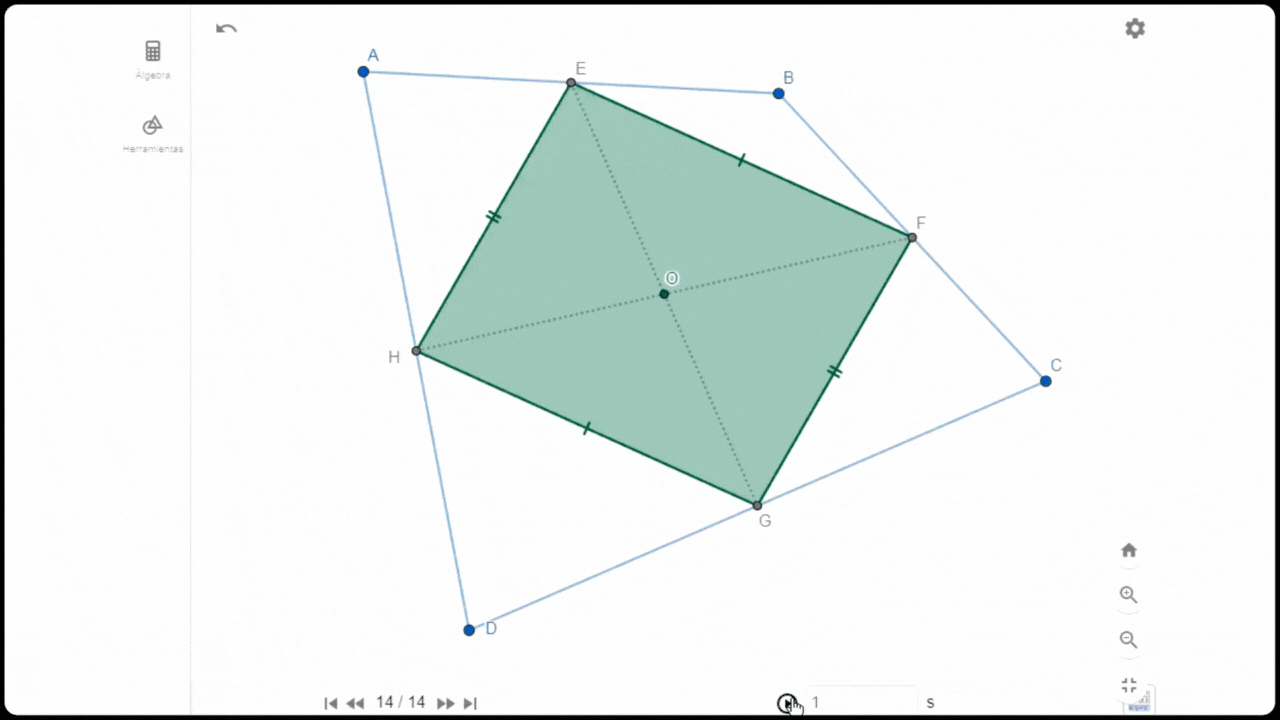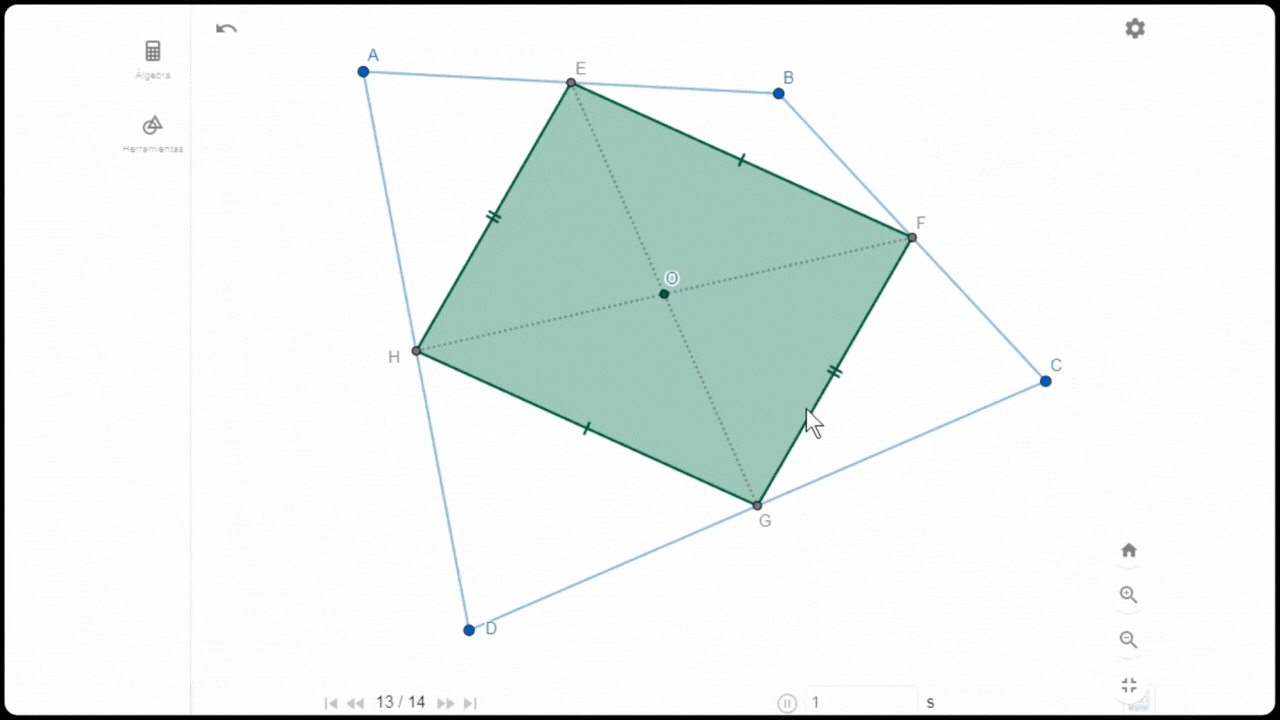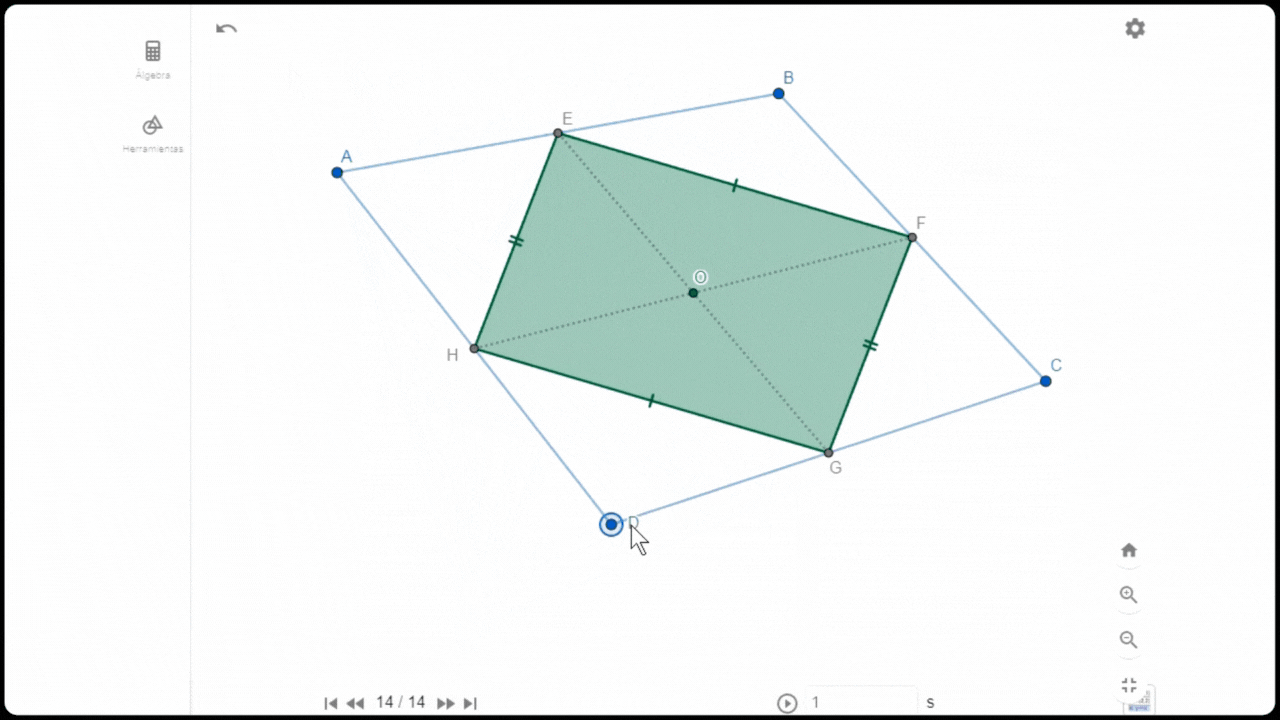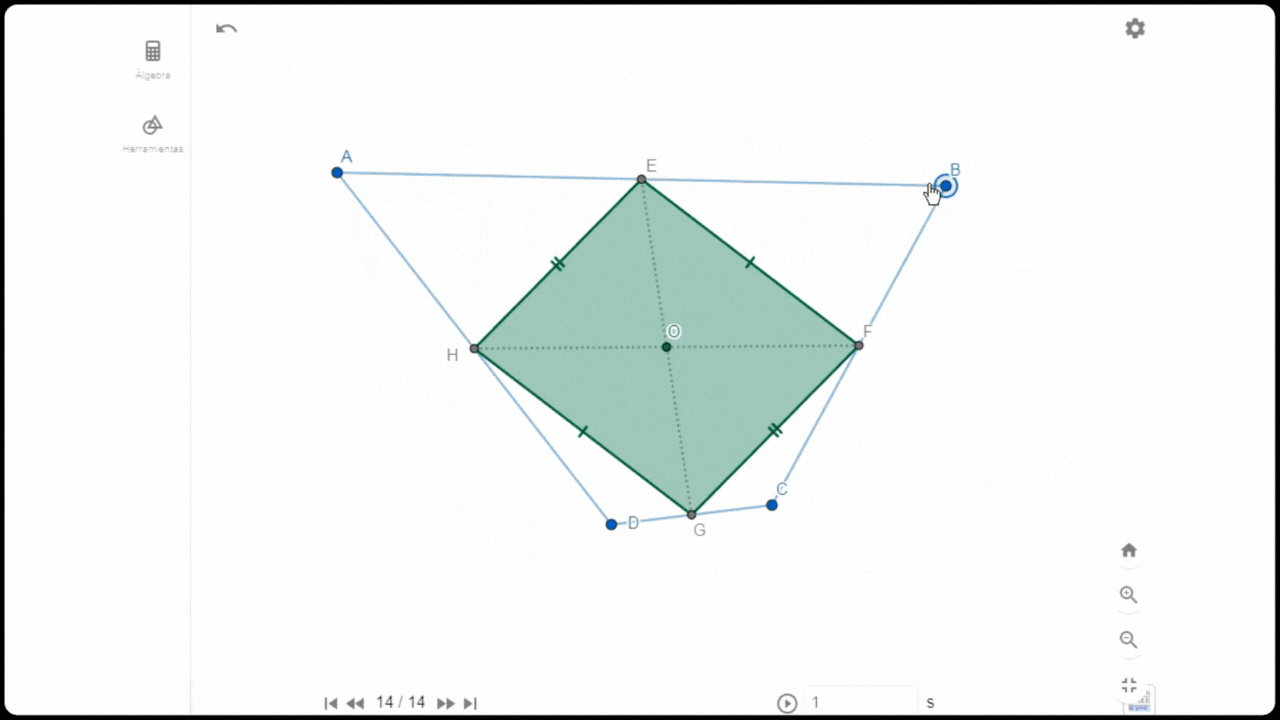_{Construcción de cometa}
Para construir una cometa dentro de un cuadrilátero arbitrario ABCD se comienza marcando los puntos medios de cada lado (mediatrices): F,G,H, y E que pasan a formar los vértices de un rombo cuyas diagonales se interceptan en un punto central O. Esta cometa tiene por característica que sus lados opuesto son paralelos y del mismo tamaño.

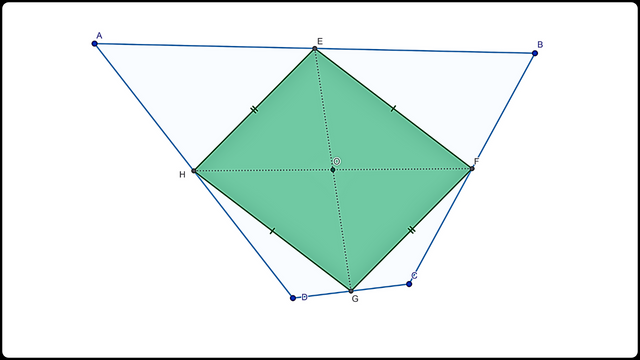_{Cometa dentro de un cuadrilátero
Construcción de cuadrilátero con diagonales perpendiculares}
Para cumplir con la perpendicularidad de las diagonales de un cuadrilátero, comencé dibujando tres vértices A,B y C del cuadrilátero. Tracé la diagonal AC y proyecté una línea perpendicular a ésta que pasa por el vértice B. El vértice D faltante lo ubiqué en dicha línea perpendicular, de tal manera que uní todo los vértices del cuadrilátero con la herramienta poligonal.

Tracé con un segmento de recta la diagonal BD y coloqué el punto de intersección de las diagonales así como la medición del ángulo recto entre ellas que se conserva independientemente del movimiento de los vértices del cuadrilátero.

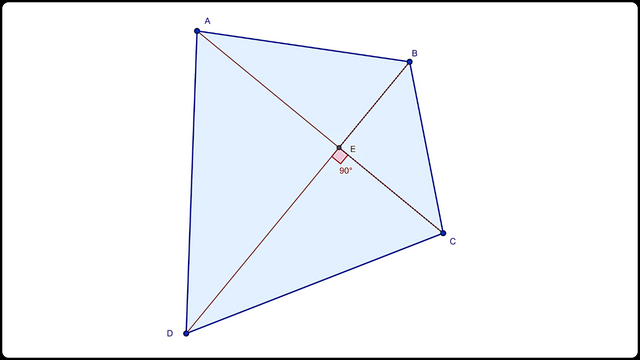_{Cuadrilátero con diagonales perpendiculares}

Notas:

📌 Imágenes propias presentadas con la aplicación canva.com
📌 Invito a participar a mis amigos @paholags @marito74 @genomil @cruzamilcar63 @dove11 @goodybest
📌 Más información del concurso en el siguiente enlace.
📌 Mi twitter: steemit_casv

¡Gracias por su visita!