SLC S23 Week6 || Geometry with GeoGebra:More on Triangles, Quadrilaterals, and Circles

We have reached the sixth and final week of the Steemit Learning Challenge Season 23, during which we will complete our introduction to basic geometric figures using GeoGebra.

Today, let's recall the things we did in previous lessons and take a deeper look at them.

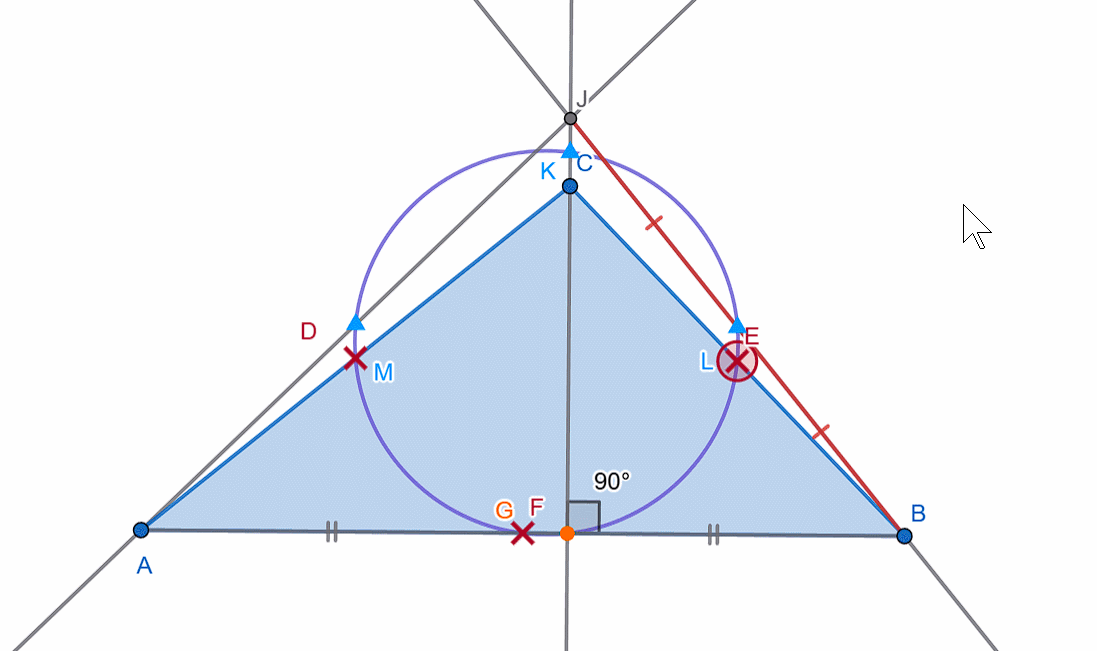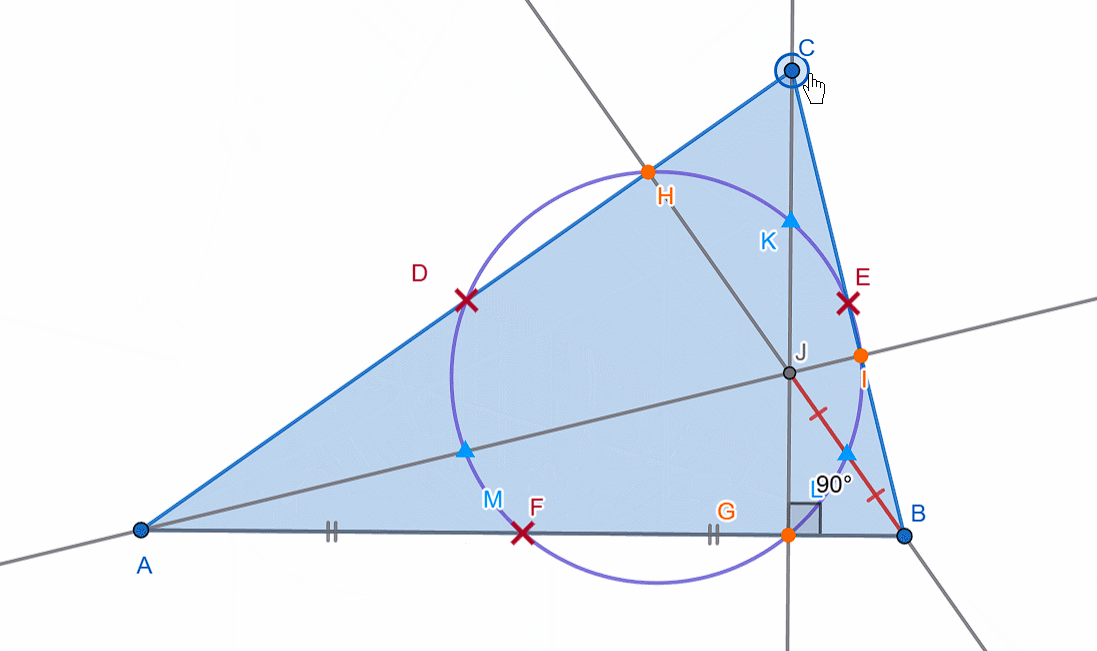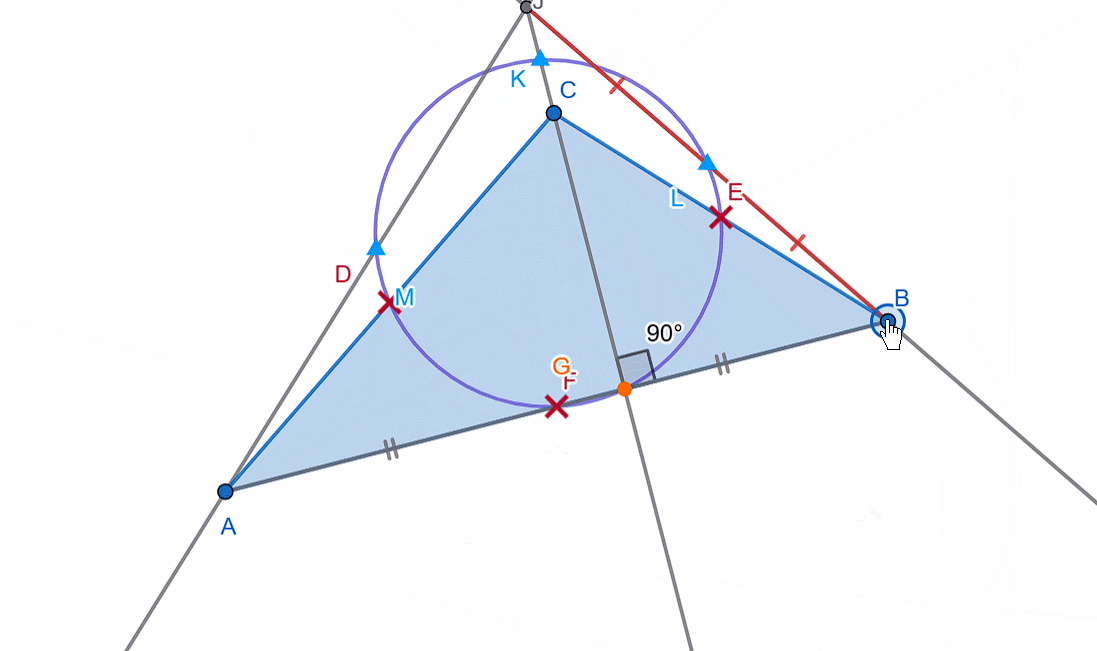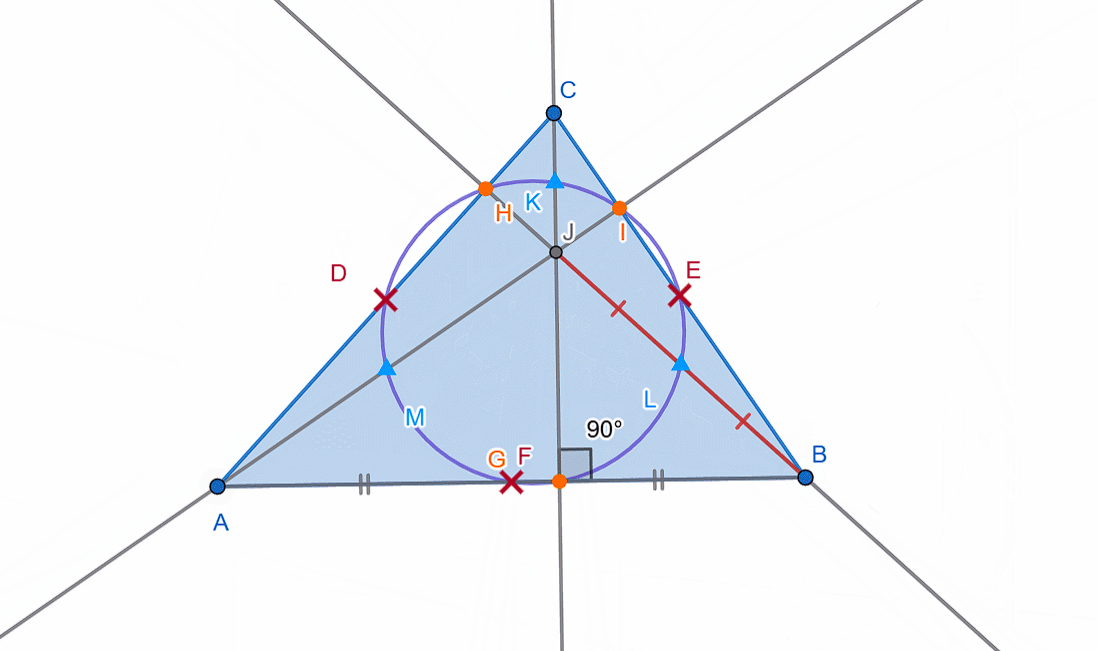
When studying triangles, we constructed inscribed and circumscribed circles. However, there are also excircles (or escribed circles). In a triangle, there are three of them, each tangent to one side of the triangle and the extensions of the other two sides.

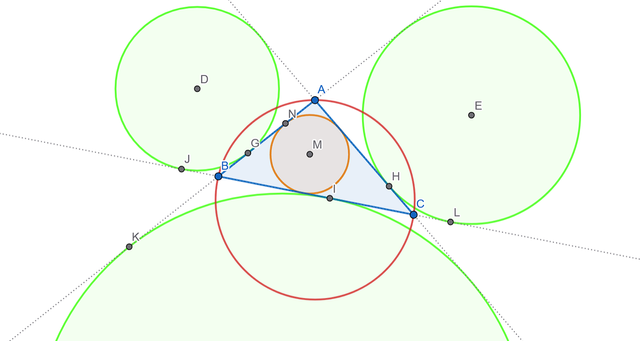
Let me remind you that the center of the inscribed circle (incenter) lies at the intersection of the angle bisectors of the triangle, while the center of an excircle (excenter) lies at the intersection of the bisectors of the external angles.

An external angle of a triangle is an angle adjacent to one of the triangle's angles, or an angle formed by one side and the extension of another side.

Additionally, there is the famous Euler's circle, also known as the nine-point circle.
The Euler's circle is a circle that passes through nine important points of a triangle:
The midpoints of the sides of the triangle,
The feet of the altitudes (bases of the heights) of the triangle,
The midpoints of the segments connecting the vertices of the triangle to the orthocenter (the point where the altitudes intersect).

The radius of the Euler's circle is equal to half the radius of the circumscribed circle (circumradius).

With quadrilaterals, the story is different. It is not always possible to inscribe or circumscribe a circle around any quadrilateral.
If a circle can always be drawn through three vertices (e.g., (A), (B), and (D)), the fourth vertex ((C)) can be:

• inside the circle,
• outside the circle,
• or on the circle.

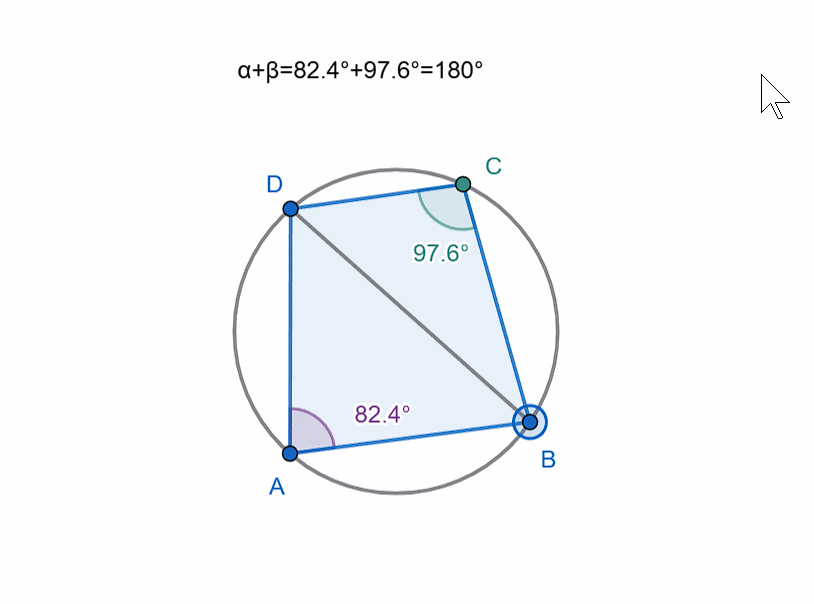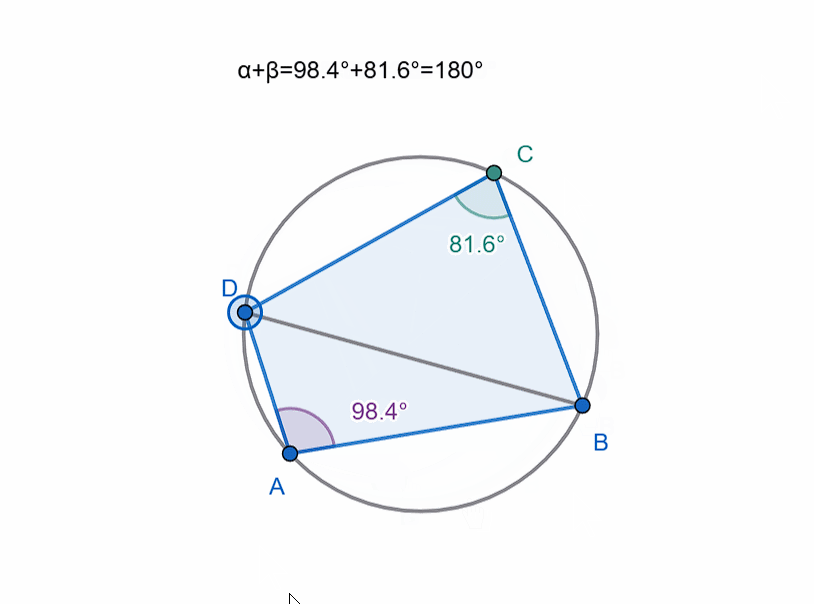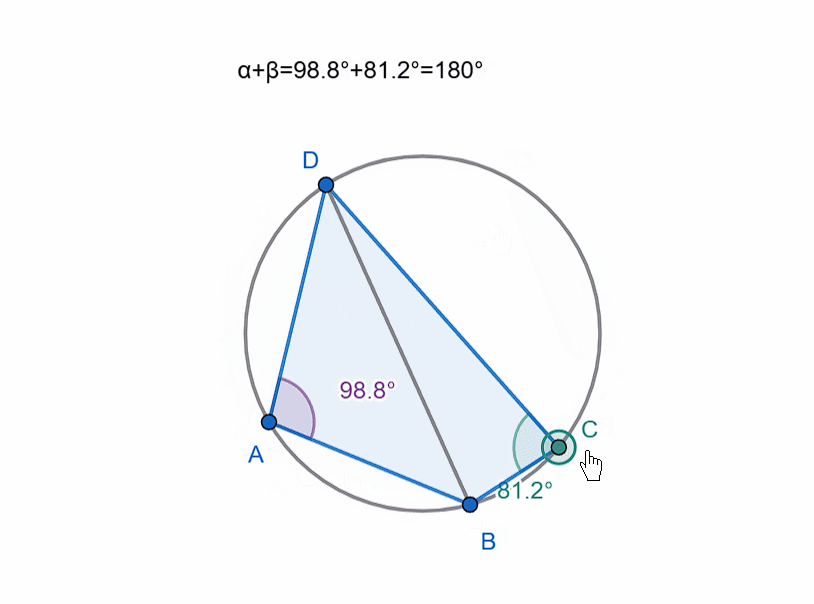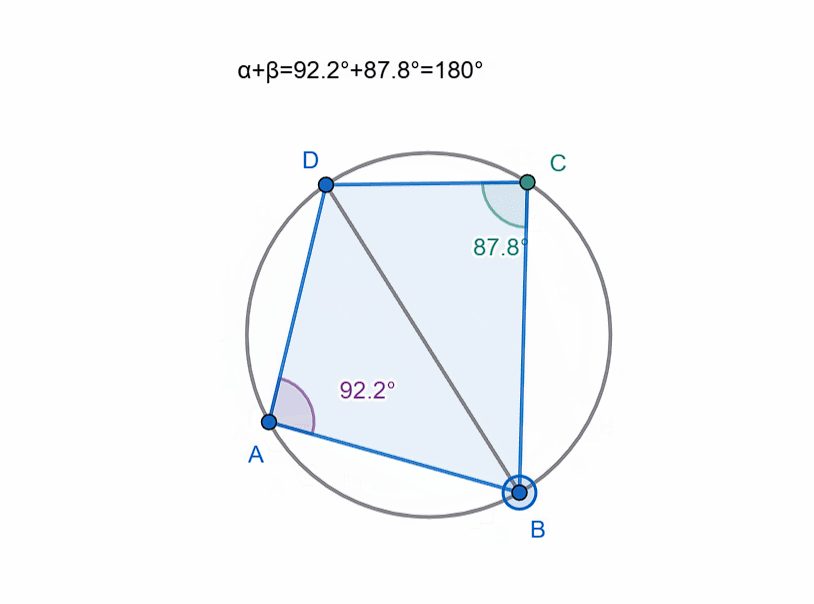
If the fourth vertex lies on the circle, then such a quadrilateral is called cyclic, and the circle is called the circumscribed circle of the quadrilateral.

If you recall the angles subtended by the same chord (specifically, the inscribed angle and the central angle), you will understand why the sum of opposite angles in a cyclic quadrilateral is 180 degrees. (The sum of the other two opposite angles will also be 180 degrees, as expected.)

However, the rule for a quadrilateral to be cyclic is as follows:
The sum of each pair of opposite angles must be equal.
In other words, for a quadrilateral (ABCD) to be cyclic, the following must hold:
∠ A + ∠ C = ∠ B + ∠ D = 180.

A circle inscribed in a quadrilateral.

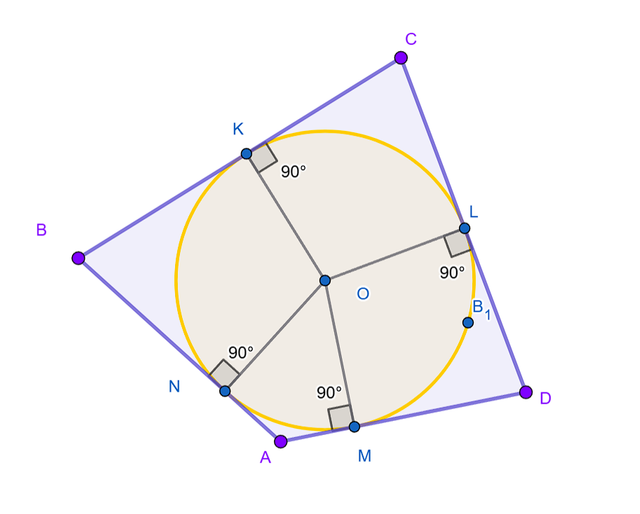
For a circle to be inscribed in a quadrilateral, it is necessary that AB + CD = BC + AD.
This is similar to the circumscribed circle—there, the condition is the equality of the sums of opposite angles, while here, it is the equality of the sums of opposite sides."

"If you take any quadrilateral and connect the midpoints of its sides in sequence, the resulting quadrilateral will be a parallelogram.

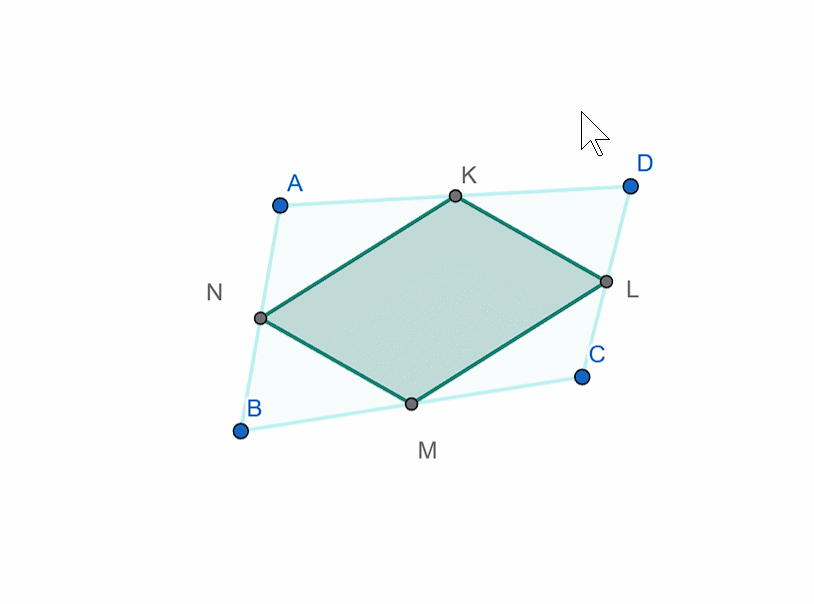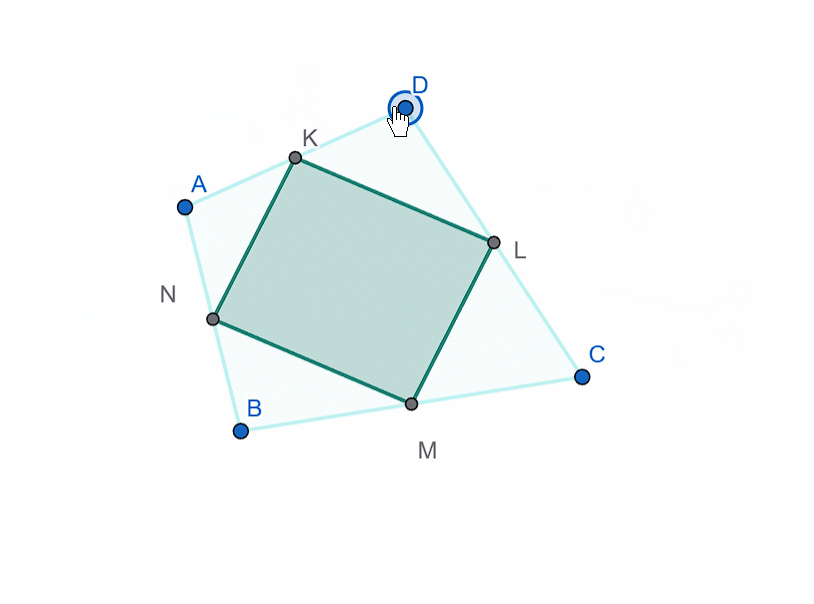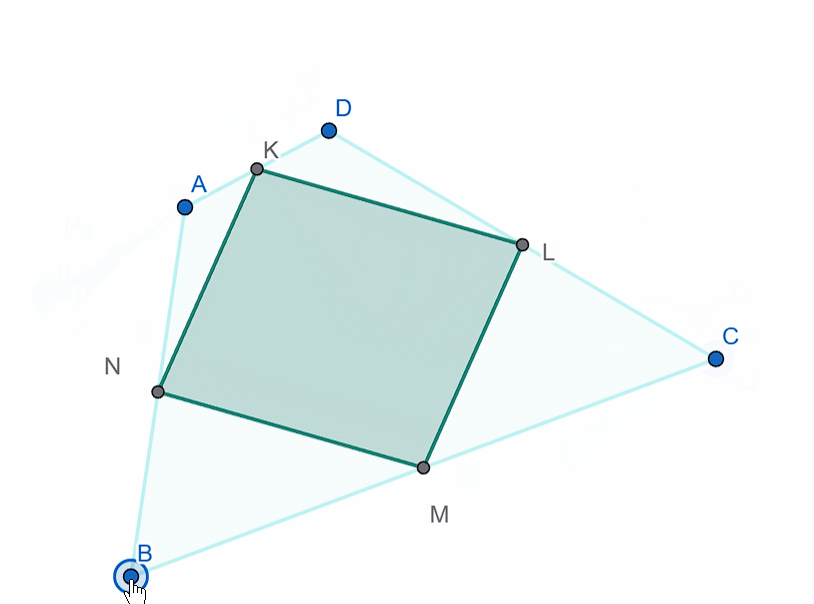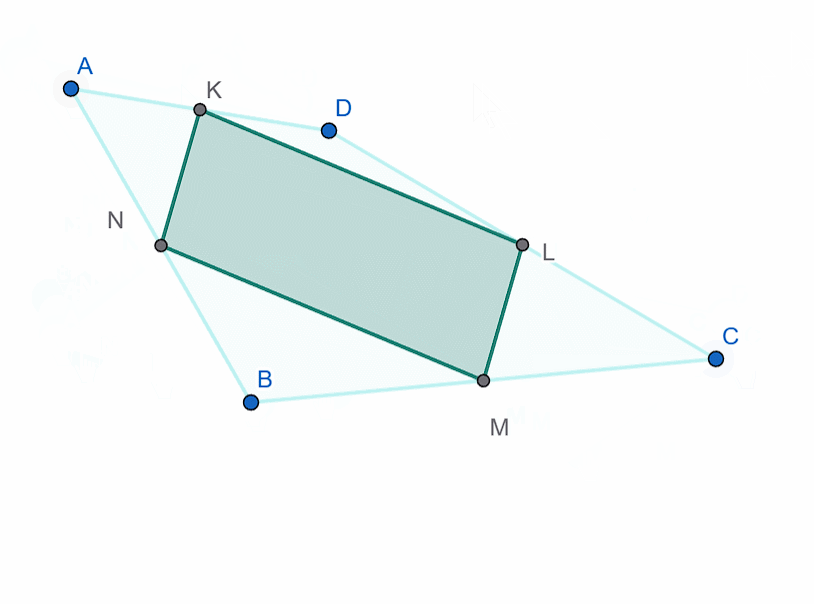
Along with the rhombus, a figure called a kite is sometimes studied. In a kite, not all four sides are equal, but only two adjacent sides are equal. The diagonals of a kite are perpendicular.

Homework:

1. Construct an arbitrary triangle, where all three vertices should be movable. For this triangle, construct its three excircles. Demonstrate how they behave.
   Bonus for additionally constructing the incircle and circumcircle.

2. Construct the Euler's circle—but better than I did, as I did not illustrate all its features—do it better than me.

3. Besides the Euler's circle, there is also the Euler line, as well as other circles such as the Spieker circle, Taylor circle, Nagel circle, Apollonius circle, Malfatti circles, and Feuerbach circle.
   Construct one of the circles I listed, or if you find another circle related to a triangle.
   Points will be lower for choosing a simpler circle and higher for a more complex one.

4. Construct a quadrilateral and circumscribe a circle around it. The center of the circumscribed circle (as in a triangle) lies at the intersection of the perpendicular bisectors.

5. Simply illustrate a quadrilateral with an inscribed circle (a picture).

6. Depict a kite and another quadrilateral with perpendicular diagonals (not a rhombus or a kite) as an animation, not just a picture.

Tasks are worth 2 points each, and the last two tasks are worth 1 point each.

Rules for Participation

Title of your work: SLC S23 Week6 || Geometry with GeoGebra: More on Triangles, Quadrilaterals, and Circles

You can publish your work in any language, in any community, or simply in your own blog. Add the link to your work below as a comment.

To help me quickly find, review, and evaluate your work, leave the link in the comment under this text, and in your work, use the tag #gwgg-slc23w6

Each task response must include at least one image and one video (GIF) demonstrating the process of construction/solving.
You can use tools like GifCam as I did.
Note: The video/GIF will have the most significant impact on the evaluation.

Plagiarism and the use of AI are prohibited.

Participants must be verified and active users of the platform.

All images used must belong to the author or be free of copyright. (Don’t forget to credit the source.)

Participants must not use any bot services for voting or engage in vote buying.

Recommend your friends to participate.

Submission Period: From Monday (March 24/2025), to Sunday (March 30/ 2025).

Your work will be reviewed, commented on, and evaluated by me. Four best works will be selected.

Good luck 🍀 on your task!

_{Posted using SteemPro}