SLC S23 Week6 || Geometry with GeoGebra:More on Triangles, Quadrilaterals, and Circles
| Assalamualaikum |
|---|
It's me @fazal-qadir from Pakistan.
How are you all? I am fine. I am hoping you all will be fine and in good health. This season was the best season for me. It was my first challenging season that I participated in. I learned about Geogebra. I never used it before. I solved each week's task with my mobile which is not mobile user-friendly. I will soon buy a laptop for it. I would like to thank our teacher @sergeyk. He guided us on each step.
Let's start the test, i am hoping I will do better in this competition.
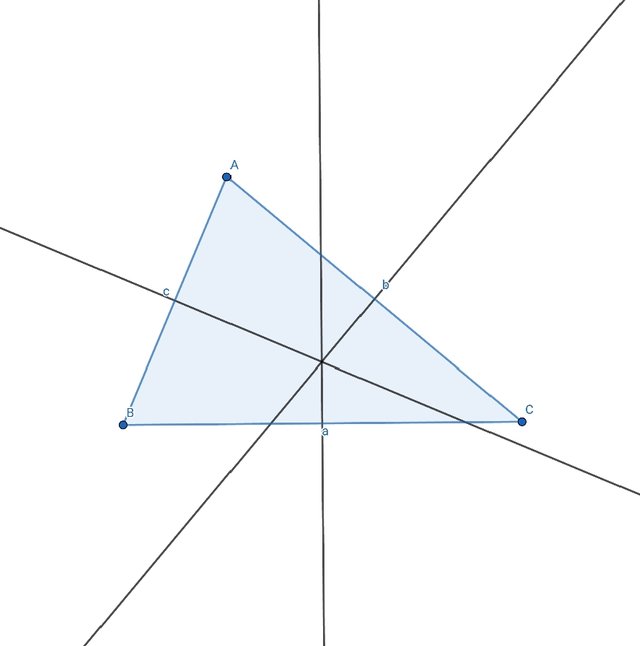
Construct an arbitrary triangle, where all three vertices should be movable. For this triangle, construct its three excircles. Demonstrate how they behave.
Bonus for additionally constructing the incircle and circumcircle.
Step 1
Incenter
We will construct an arbitrary triangle for it we will use the polygon tool.
We will take point A,B and C.
Step 2
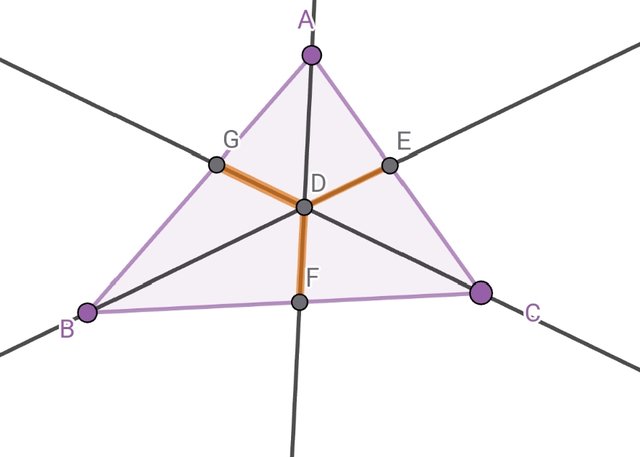
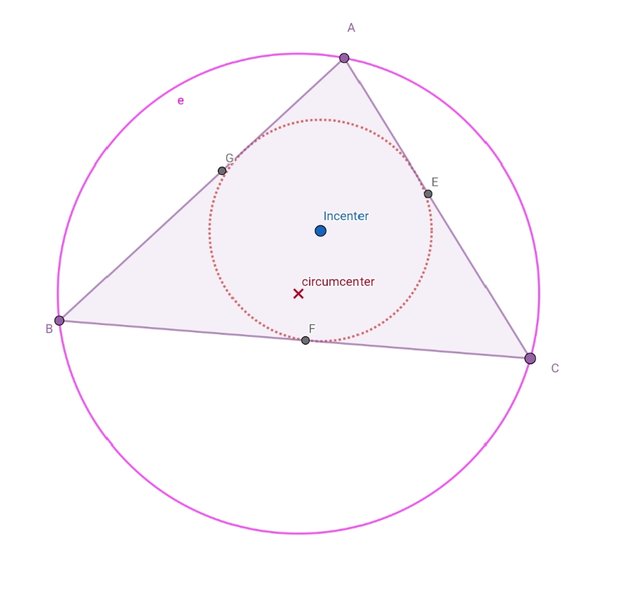
We will draw the incircle. For this we will need all three angle bisectors. After that we will use the intersection tool to find where the angle bisectors intersect. That point is known as the incenter.
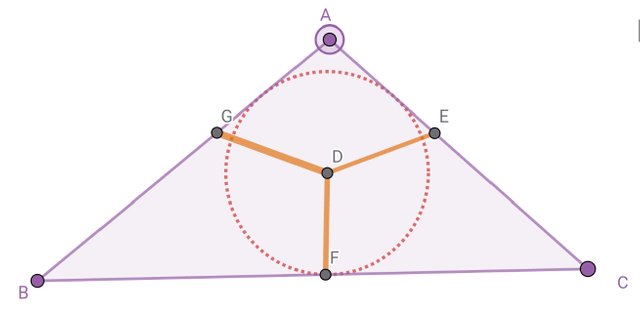
After that we will use the perpendicular line tool to draw one perpendicular line joining the point of intersection with the center.
Now we will use the circle tool to create the circle within the triangle.
Diagram 1:
Explanation:
Here I used Angle Bisector tool to draw all three angle bisectors. Used Intersection tool the point D is the point of intersection of all bisectors. After that I used the Segment tool to draw all three segments and colored them with light brown color.
Diagram 2 .
Explanation:
We will take the Perpendicular Line tool. Using the Intersection tool, take the point of the perpendicular line and side intersection point. Here we will use the Circle tool to draw the circle inside the triangle, which is called the incenter. We will use the Hide tool to hide the extra lines.
Circumcircle
Step 1
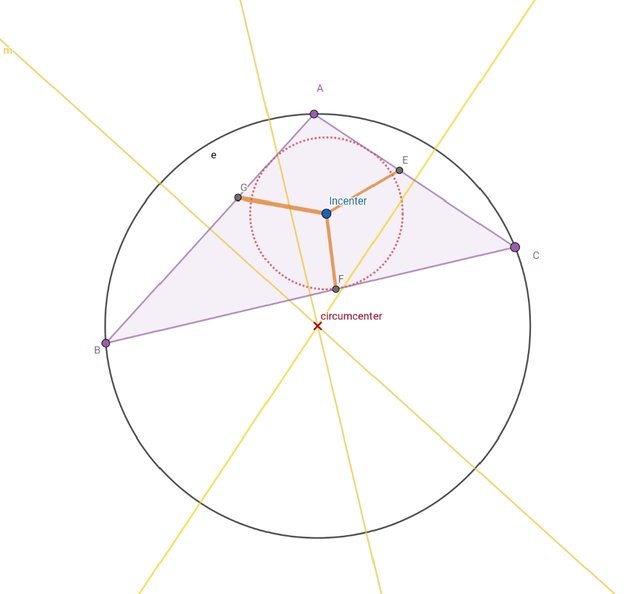
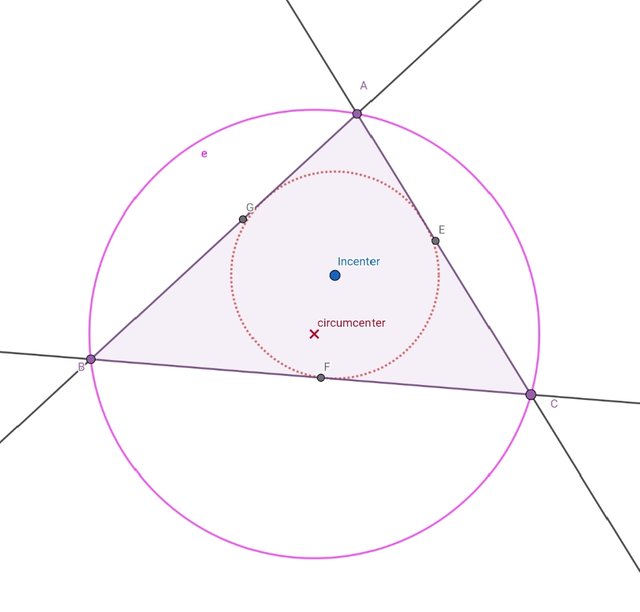
While drawing circumcenter , we will draw a triangle using polygon tool . After drawing triangle we will use perpendicular bisector tool and draw three perpendicular tool . Where all the three lines intersect. That point is called the circumcenter. Using circle tool , we will draw the center. That circle is the required circle called circumcircle.
Diagram 1:
Diagram 2:
Here I hide all the extra lines . And you can see the circumcenter in it. I also drawn the circumcircle.
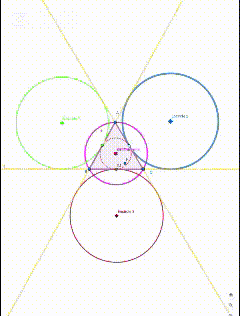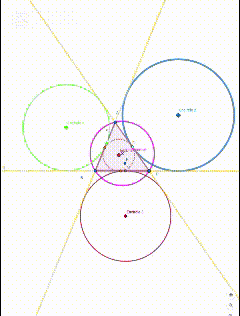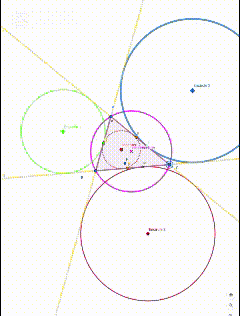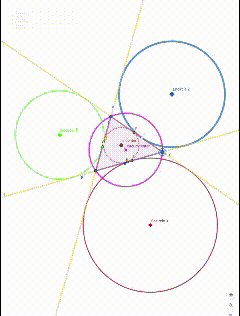
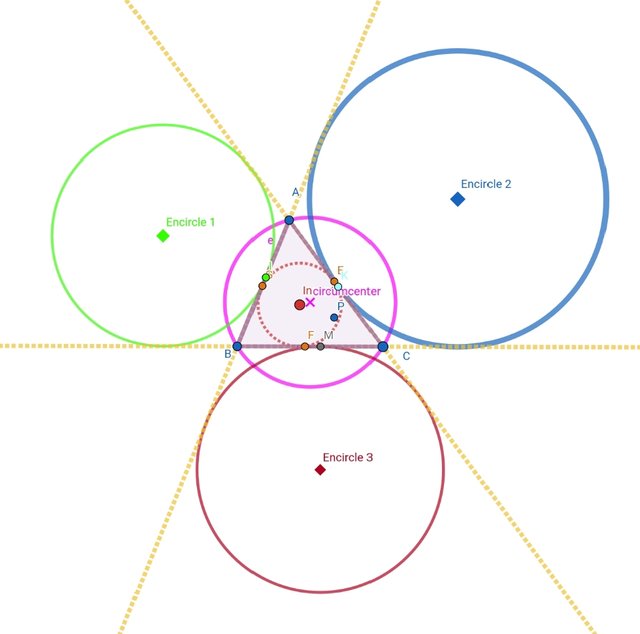
Three encircles
Here I will explain one encircle steps only , that how I done it.
After that I will show the final image at the end.
Step 1
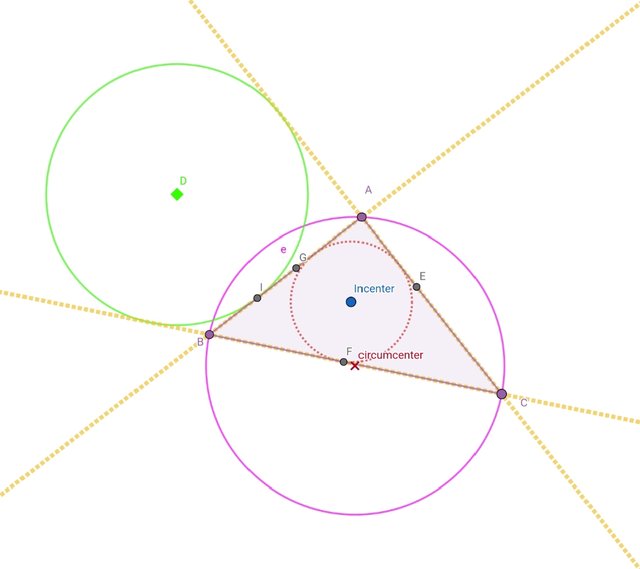
First of all I will draw the line tool and will draw the lines .
Click at point A and point B a line will be drawn. Same goes for other lines. Click two points if you want to draw the lines. Draw all the three lines.
Diagram 1:
Diagram 2:
Explanation:
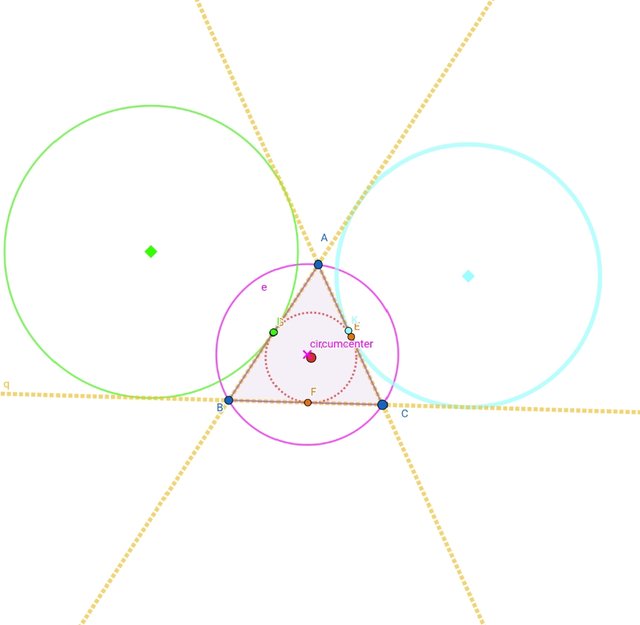
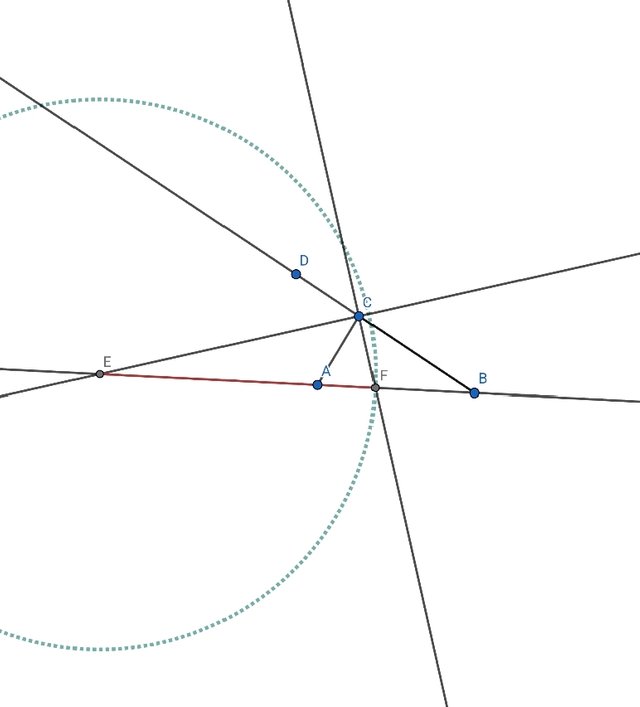
Now I will take two angle bisectors. For it you will need three points or two lines. As we can see we do not have three points so I will take two lines. After drawing two angle bisectors, the point of intersection using Intersection tool I mark it. Now we will need one perpendicular line. So we will use the Perpendicular Line tool. Click on the point of intersection and the line of the triangle opposite to it. After taking perpendicular line, use the Segment tool. Take a line segment, after that use the Circle tool to draw the excircle. That's it. That excircle is the required circle for us. Follow these all steps to complete the task and draw all three excircles.
Diagram 3:
Final image:
| GIF |
|---|
 |
|---|
| YouTube |
|---|
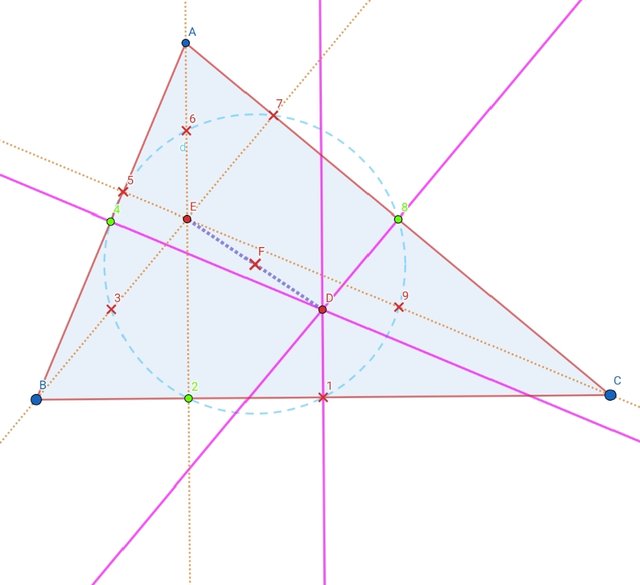
Construct the Euler's circle
Steps:
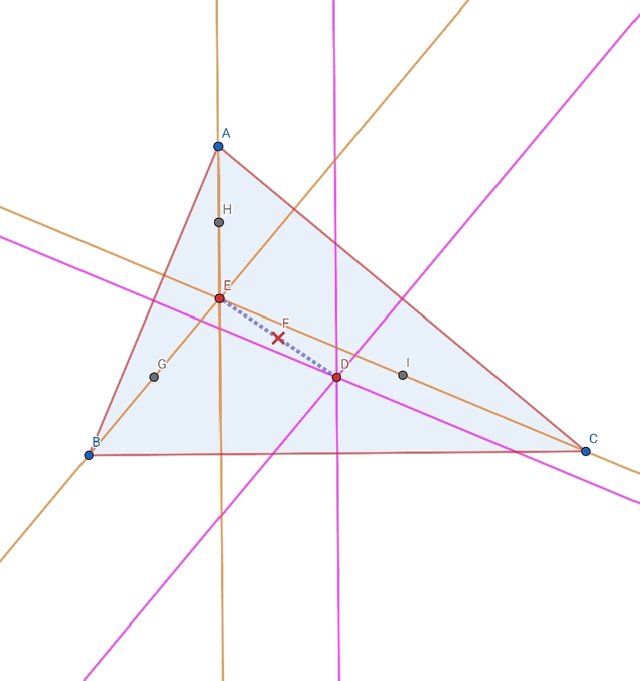
To draw Euler's circle first we will draw triangle. For it I used Polygon tool, draw arbitrary triangle. First we will need three perpendicular bisectors. We will draw the three perpendicular bisectors using Perpendicular Bisector tool. Take the point of intersection of the three perpendicular bisectors. Now we will apply Perpendicular tool to draw three perpendicular lines is not needed. Point out the intersection point of three perpendicular bisectors.
Diagram 1:
Draw the three perpendicular bisectors.mark their point of intersection.
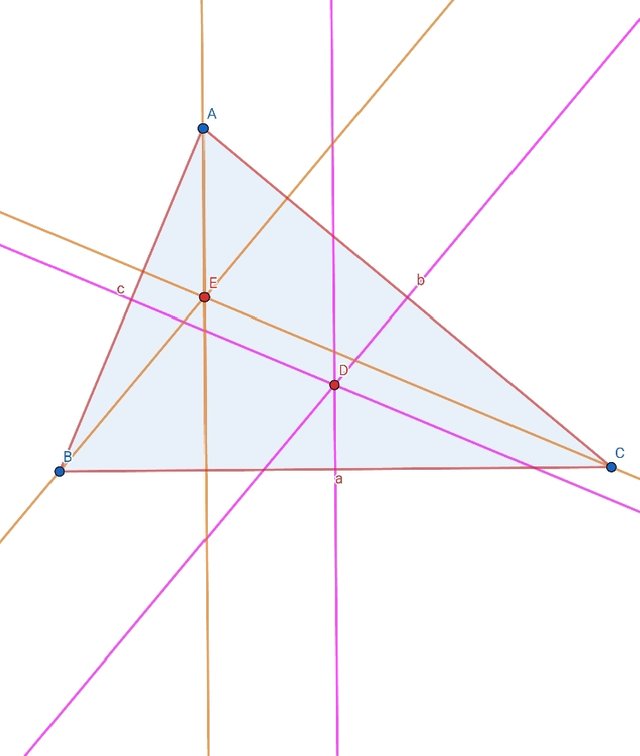
Draw the three perpendicular lines. Mark their point of intersection using intersection tool. That point is called orthocenter.
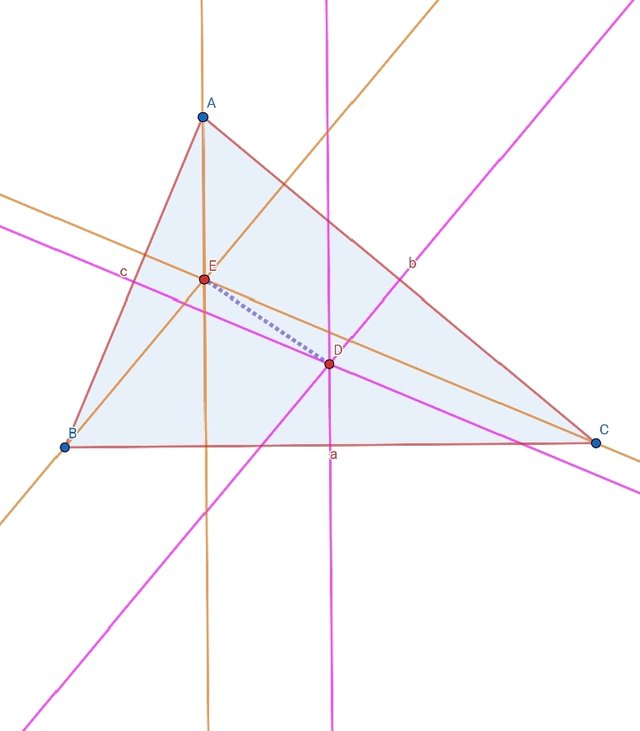
Joing both point of intersection E and D using segment tool.
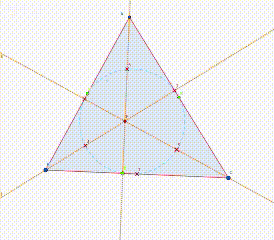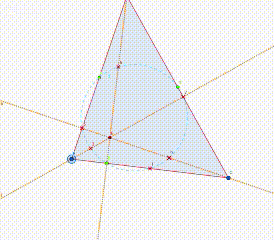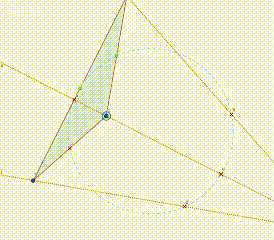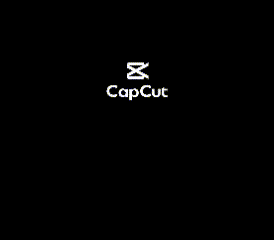
Find the mid point of these two intersectionE and D. Also find the mid point from the orthocenter E to all three vertices A,B,C.
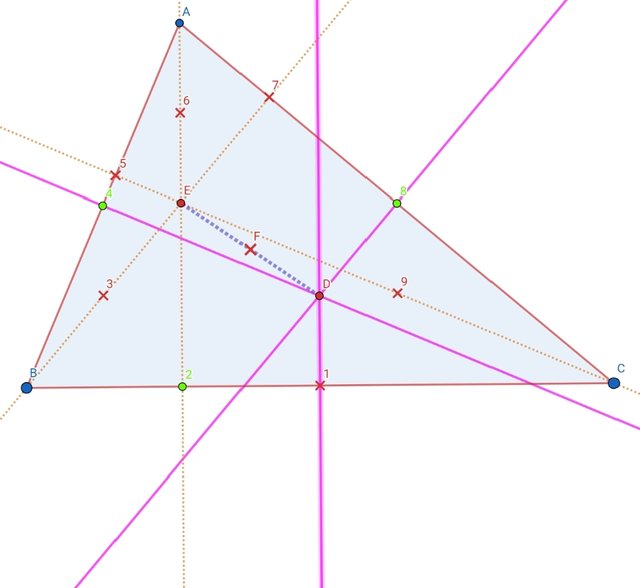
Here mark all the mid points and all foot of altitude.
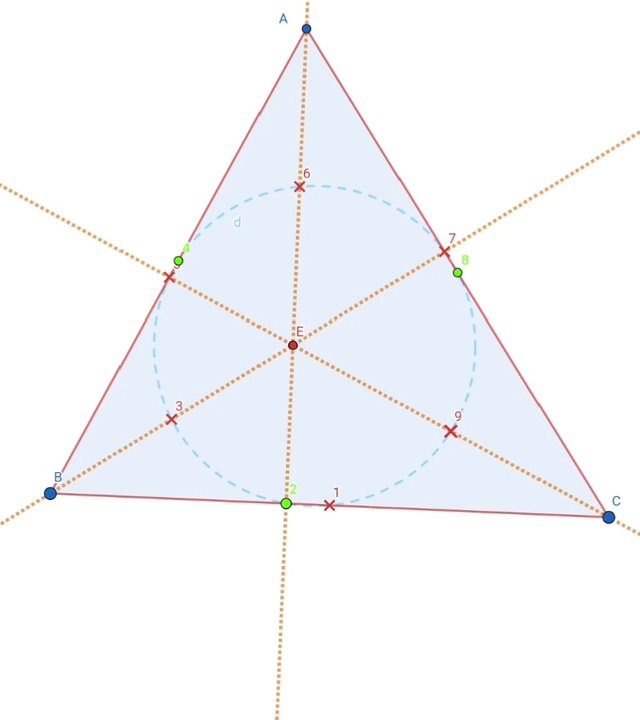
These are total 9 in numbers. I marked from 1 to 9. That's why this is also called 9 point circle.
From here draw the circle from the center F. Using circle tool.
Hide all perpendicular bisector lines and their point of intersection. Also hide the center of triangle.
This is the final form of the Euler's circle.
| GIF |
|---|
 |
|---|
| YouTube |
|---|
Besides the Euler's circle, there is also the Euler line, as well as other circles such as the Spieker circle, Taylor circle, Nagel circle, Apollonius circle, Malfatti circles, and Feuerbach circle.
Construct one of the circles I listed, or if you find another circle related to a triangle.
Points will be lower for choosing a simpler circle and higher for a more complex one.
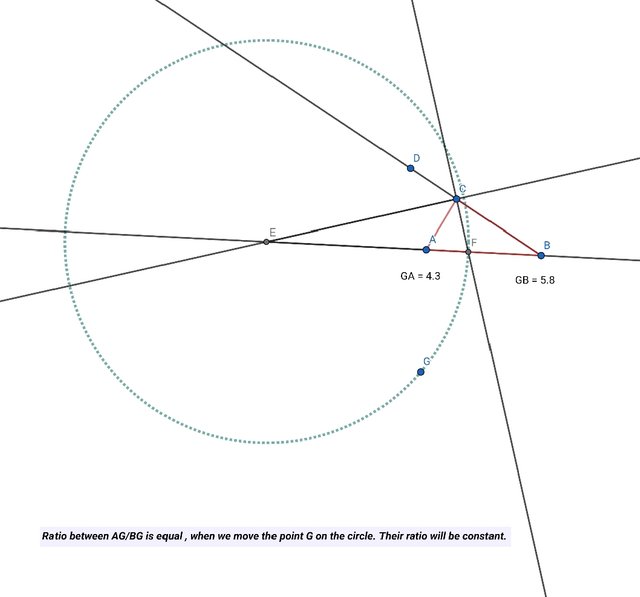
Apollonius circle
Steps
Explanation:
Take two points A and B. Use Line tool to draw from point A to B. Take a point C. Use Line Segment to join C to A and B. Draw a ray from B to C. On that ray take a point D. Find angle bisector on DCA. Use Intersection tool to mark that point which is E. Take another angle bisector on ACB. Mark the point using Intersection tool and label it point F. Now take a line segment from point E to F. Use Circle tool to draw a circle making E as center and the end point should be F. Take any point on the circle. I take point G on the circle. Now find the distance from point A to G and from B to G. Find the ratio between AG and BG. When we move the point G on the circle the ratio will not change. It will be fixed.
Diagram 1:
Diagram 2
Diagram 3
Diagram 4
Diagram 5
Diagram 6:
| YouTube |
|---|
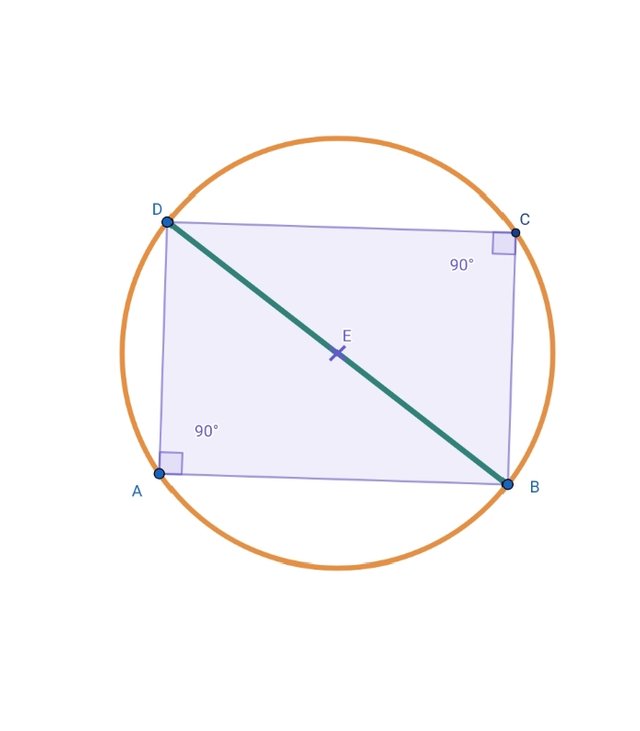
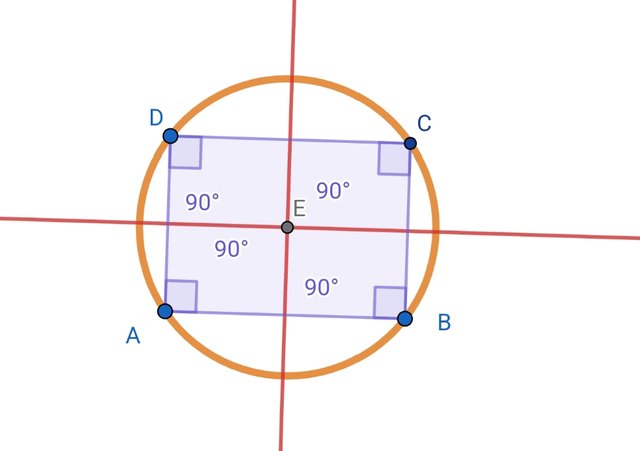
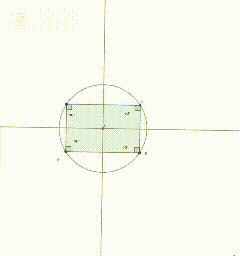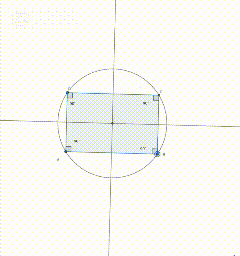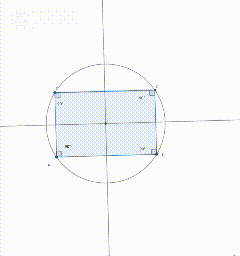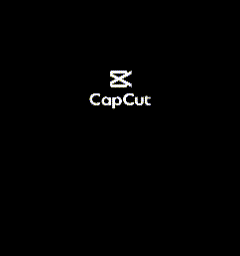
Construct a quadrilateral and circumscribe a circle around it. The center of the circumscribed circle (as in a triangle) lies at the intersection of the perpendicular bisectors.
Quadrilateral:
Quadrilateral is a polygon which have four sides.
Steps
Take two points , apply line tool. Take one point C Draw a perpendicular line . Take parallel lines and draw another line CD. Another perpendicular line to complete the quadrilateral.
Now take perpendicular bisector on side AB and another on side BC. Mark the point of intersection with intersection tool. Apply circle tool now to complete the circle.
| GIF |
|---|
| GIF |
|---|
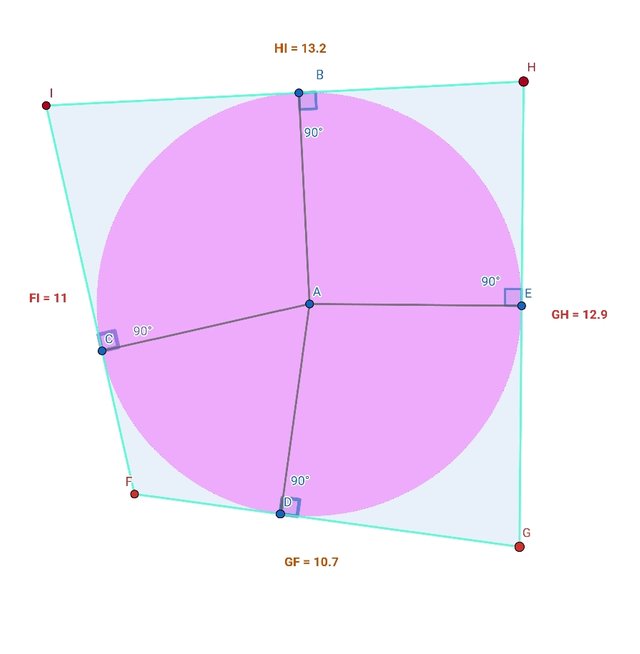
Simply illustrate a quadrilateral with an inscribed circle (a picture).
Explanation:
Draw a circle. Take 4 random points on the circle B C D and E. A is the center of the circle. Use Tangent tool click on the circle and then at the points B C D and E respectively. Use Intersection tool to mark all the tangents intersection point. F G H and I are the vertices of the quadrilateral. I measured the length of the side FG + IH = FI + GH. This is known as tangential quadrilateral.
Task 6
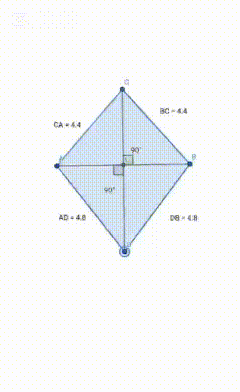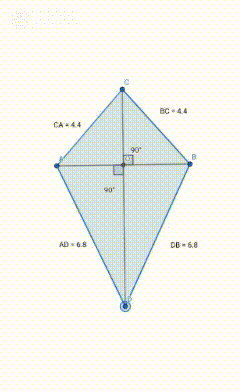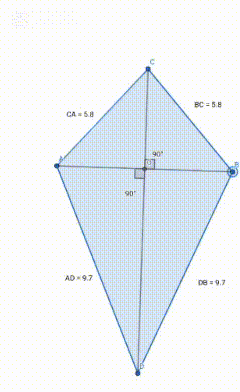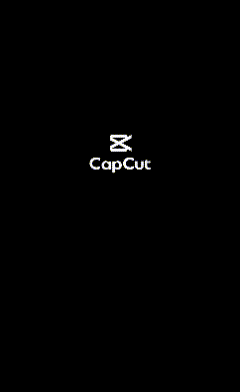
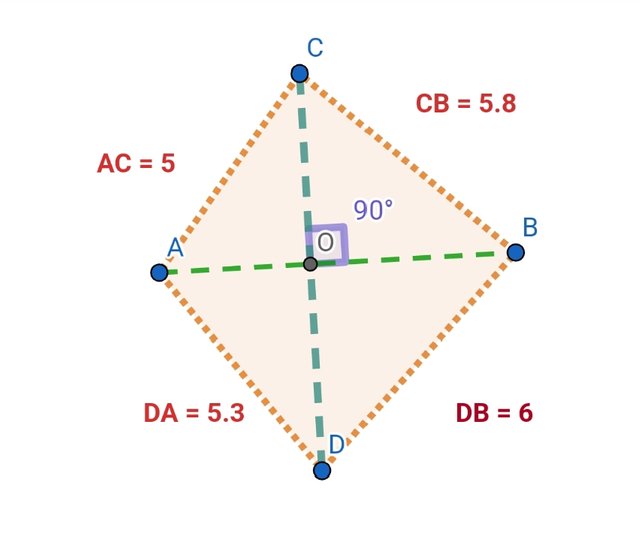
Depict a kite and another quadrilateral with perpendicular diagonals (not a rhombus or a kite) as an animation, not just a picture.
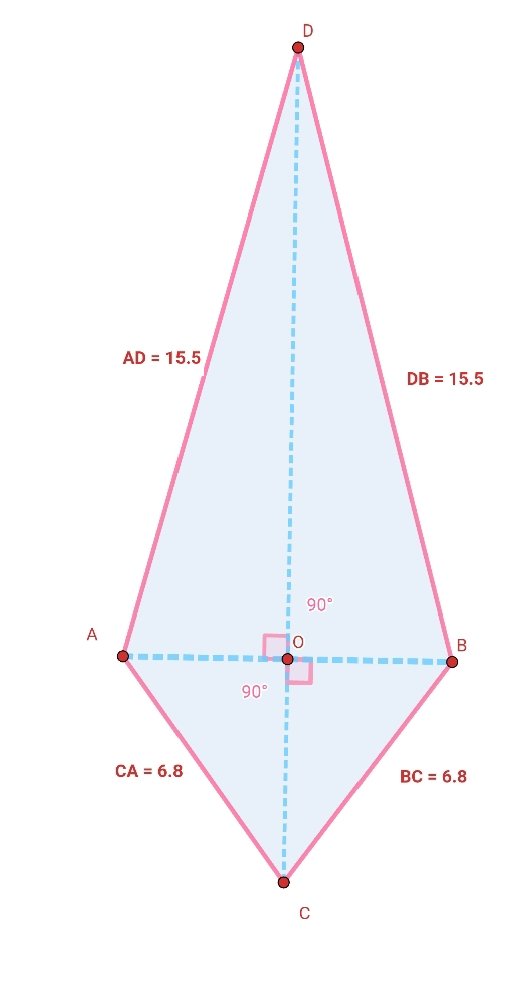
Part 1 (kite quadrilateral)
The above diagram is of a kite quadrilateral, as you can see the perpendicular diagonals are showing equal angles.
Also if we add the two adjusent side the sum is equal to the other two adjust side sum.
AC+AD =CB+BD
It shows that it is kite quadrilateral.
| Gif |
|---|
| YouTube |
|---|
Part 2 (Random quadrilateral)
Here I take one line using Line tool and draw a perpendicular but not at the mid point of the first line. I mark a point where the line and perpendicular line intersect and mark it as point O. I took two points C and D such that the distance from CO is not equal to DO. Same as the distance from AO should not equal to BO. As we can see from the diagram. Sum of adjacent sides are not equal so we can say it is not kite quadrilateral also not the rhombus quadrilateral. Diagonals are perpendicular.
| GIF |
|---|
| YouTube |
|---|
Thank you again sir for organizing this challenging competition for us. I tried my best to come in top 4. All the participant were highly qualified and experience candidates. So I fail from very low margin. That's life sometimes you win sometime you lose. At the end I would say, I have learned anythings from you. I will be desperately waiting for the next season. Take care.
I would like to invite the following fellows.
@yousafharoonkhan @genomil and @@@ulfatulrahmah
Best regards,

Upvoted! Thank you for supporting witness @jswit.
@tipu curate
Upvoted 👌 (Mana: 0/7) Get profit votes with @tipU :)
Thank you for your support
Hi @fazal-qadir, Please you must share this post on Twitter (X). Check the post below to learn how to share your post on Twitter. This POST LINK is a guide to that effect.
https://x.com/fzllala/status/1906284055399665867?t=cIxjFP0us8qVaCgaWaEZcw&s=19