Calculate the volume of a solid of revolution using the method of disks

Being able to calculate the volume of a solid in revolution is another of the many applications that the integral has, we know that one of the applications is the calculation of the area of the intersection between two curves, the purpose of this post is to explain how we can use the integral to calculate the volume of a solid in revolution by means of the integral.

The importance of calculating the volume of a solid in revolution in engineering for example, is that many of these solids are used in engineering, an example of them is the case of a funnel that in petroleum engineering is used to calculate the viscosity of fluids.

Image source

Another example of a solid in revolution is that of a piston, which is widely used in mechanical engineering for combustion engines:

Image source

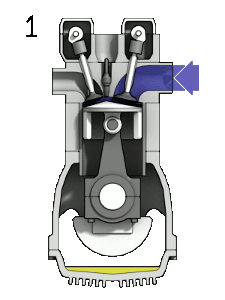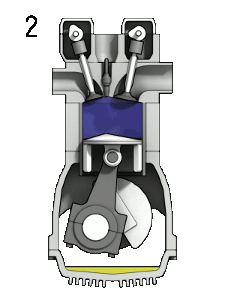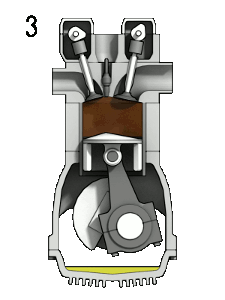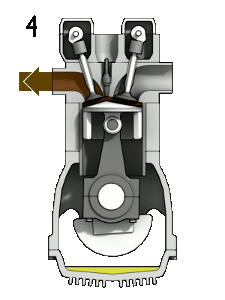
Due to these uses in engineering is that they can be studied by means of integral calculus to calculate their volume, in this technical case by means of the method of disks.

It is called the disk method, because if we rotate around the x-axis or y-axis a region of the plane, a solid in revolution is formed in the form of disks.

Image source

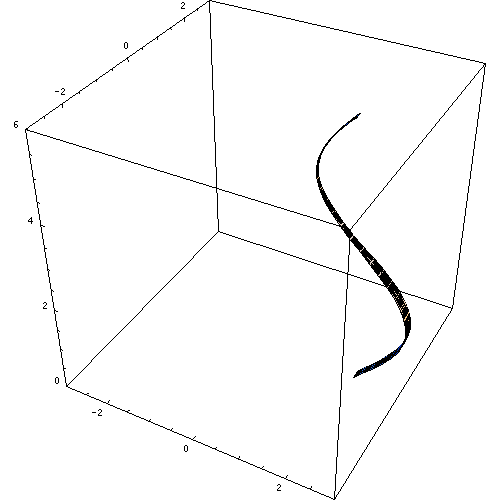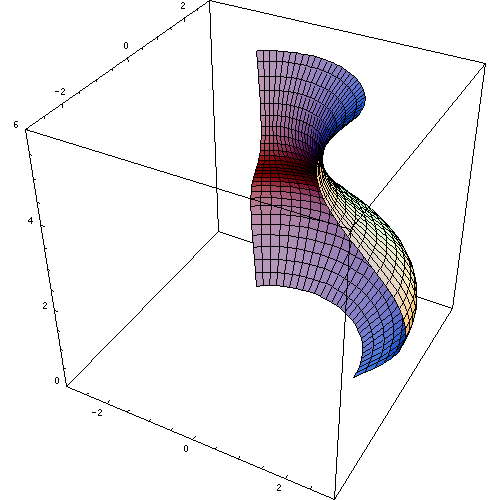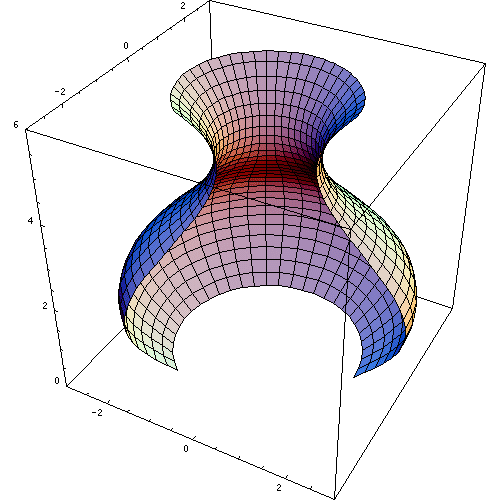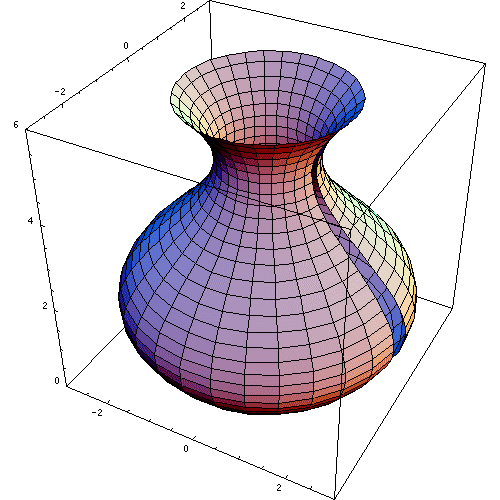
Disc method

To obtain the volume of a solid in revolution, i.e. the volume of a figure in the (x,y) plane rotating around an axis by the method of disks, a formula is used for when the axis of revolution is horizontal, and another formula is used for when the axis of revolution is vertical:

Horizontal axis:

Vertical axis:

Use of the integral in the application of the volume calculation by the method of disks.

Calculate the volume of the solid formed by rotating the region around the x-axis of:

f(x)= -x + 1

Let's see what the region of the plane is:

When this region in X from 0 to 1 and in Y from 0 to f(x)= -x + 1 rotates around the x-axis, the following solid in revolution is formed:

Conclusion and analysis

The method of layers is a very useful method to apply when the region of the plane is a function that when rotating around an axis generates a solid in revolution, later we will see which method can be applied when the region of the plane can be the intersection of two functions.

Consulted and recommended biography

Book of calculus with analytic geometry by Larson and Hostetler. Volume I. 8th edition.

Note: The equations used in this publication were elaborated using the equation insertion tools of Microsoft PowerPoint. The images without fonts were elaborated using Geogebra software and Microsoft PowerPoint.