THE HARDY-RAMANUJAN NUMBER
It is the smallest nontrivial taxicab number, i.e., the smallest number representable in two ways as a sum of two cubes. It is given by
1729=1^3+12^3=9^3+10^3.
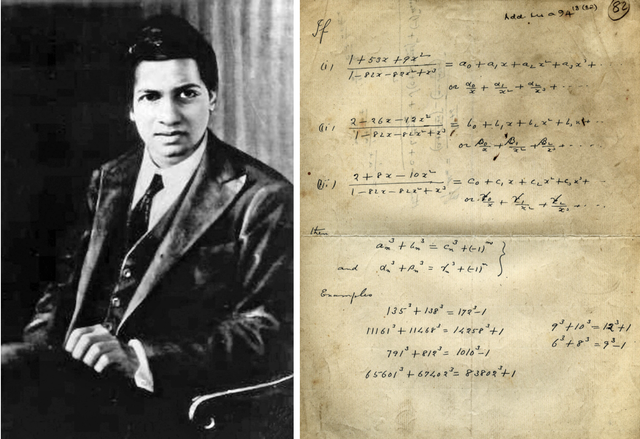
The story behind it...
"I remember once going to see him when he was ill at Putney. I had ridden in taxi cab number 1729 and remarked that the number seemed to me rather a dull one, and that I hoped it was not an unfavorable omen. “No,” Ramanujan replied, “it is a very interesting number; it is the smallest number expressible as the sum of two cubes in two different ways." - G.H Hardy
SOME INTERESTING FEATURES OF "1729" :
- First Carmichael number.
- First absolute Euler pseudoprime.
- Also the first Ziesel number, and many more.
Seems Interesting.!! @bib15hash
Indeed it is..!!
@boss.baby