SLC S23 Week 2 || Geometry with GeoGebra; The triangle and its Elements.

Hello friends and welcome to my blog and I would love to welcome you to the SLC S23/W2 and would love to give great accolades to the professor @sergeyk for such an interesting lesson and i would definitely take part in these tasks too.

---

TASK 1: Build a Triangle with 3 altitude

---

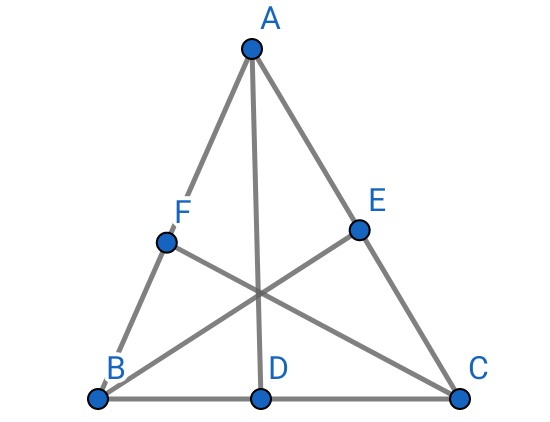
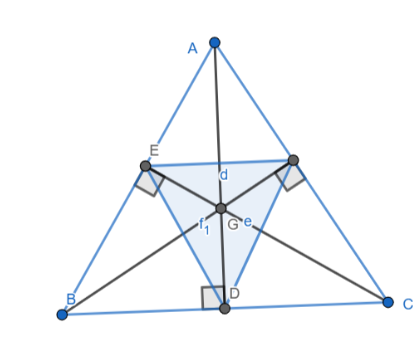
I visited the GeoGebra application on my phone after downloading it for this task and I selected the special points and they were joined using good segmented lines. These altitude was formed by drawing perpendicular lines across the opposite points of these special points. Construction of the altitude was chosen and perpendicular lines icon chosen which crossed across vertically and diagonally respectively to form 3 different lines having a confluence at the center.

---

TASK 2: Comprehensively Build a Triangle

---

Performing the series of activities I selected 3 special points joining them with segmented lines respectively and immediately using perpendicular lines across each opposite points forming my altitude. The angels could be visibly seen as the lines fall perfectly in place. The special beauty would be to isolate each perpendicular line by using special colors.

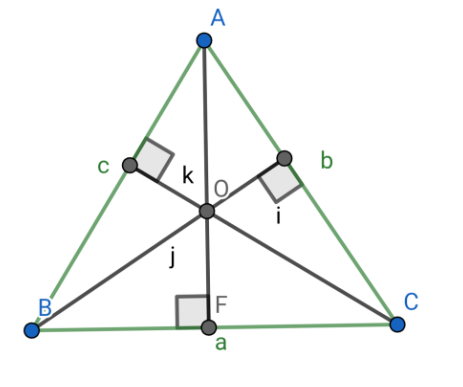
Median Line: We seek for midpoint between BC ad give it suitable label, the selected segment line you observe point A and move to point M this creating medium. We further select distance tool to ensure distance between BM equals between CF.

Angle Bisector: Select B, A and C creating Bisector for BAC triangle highlight AB and point A, the angle Bisector and show angles are equal to AC, we turn it to something special by diversifying the colors effectively.

---

TASK 3: The Basics Concepts of Median

---

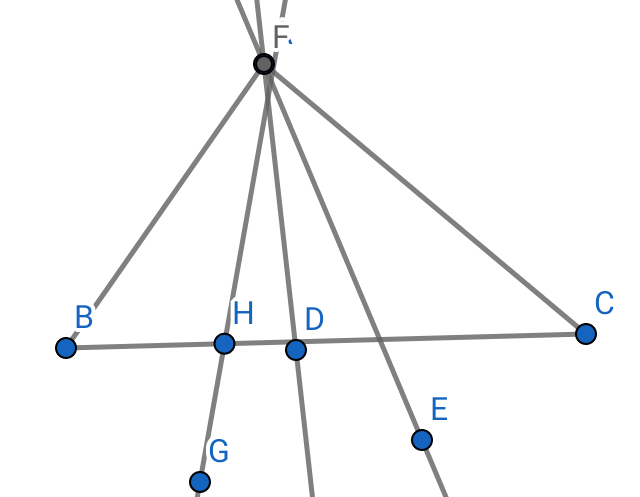
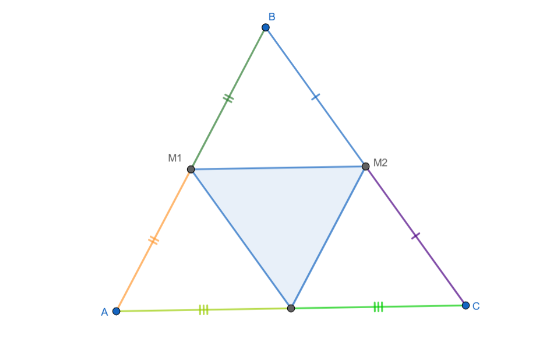
We construct triangles after selecting the three special points and using segmented lines to join ABC, Perfectly find out the midpoint of AB, BC and CA respectively using center Icon, label midpoints M1, M2, M3 using line segment to thus connect these points, we press hold each segment, proceed to object properties, style and decoration to show the sides of the halves are equal.

Distance tool is used to measure length of triangles to compare it to a perfect triangle. Angle tool would be used to measure angle to triangle. M1, M2, M3 to compare each triangle to ABC. Observation fins out that AM1M2C forms parallelogram and the rest of construction point B angle is equal to M3, angle A is equal to M2 and C equal to M1.

---

TASK 4: Bases Of Altitude

---

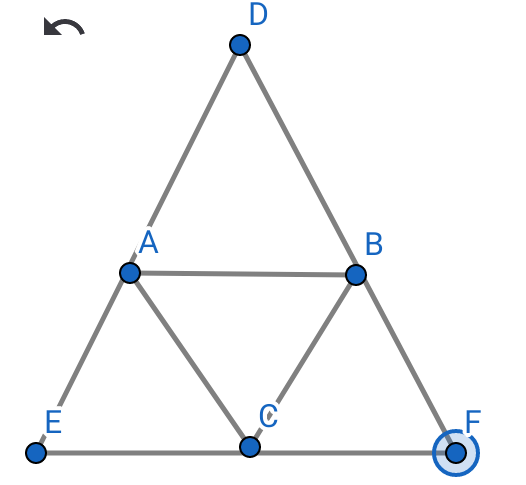
We pick these special points and join with segmented lines, we construct altitude between BC, AB and AC respectively, the bisector line is joined with line segment poing where altitude meet is the controit called G

Another triangle is incorporated into this particular one, it is adjusted by more icon to fit in at the vertex. An angle of 90° is made thus really shown below.

---

TASK 5: Bases Of Angle Bisectors

---

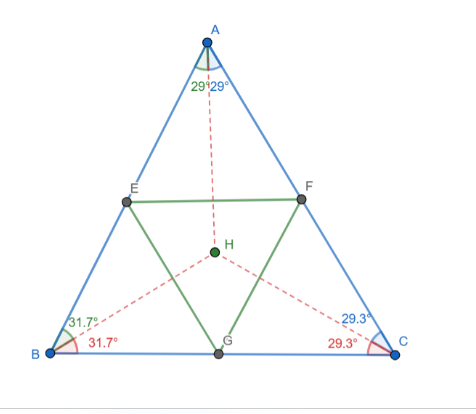
We pick these special points and join once an with segmented lines, using angles bisector for each point. A B C respectively the verticles of the angle are spotted, we move forward for the triangle proper.

We demonstrate angle on bisected angle, locate centroid of bisector, use segment line to create lines to center underlying properties going to use dotted lines to replace original, we immediately measure angle for each of the sides and show all divided evenly using angle too.

---

TASK 6: Application of combination of all

---

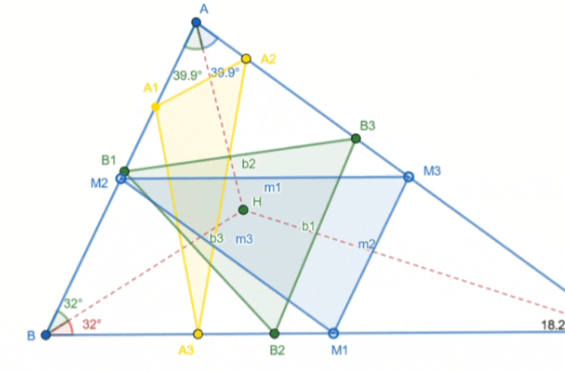
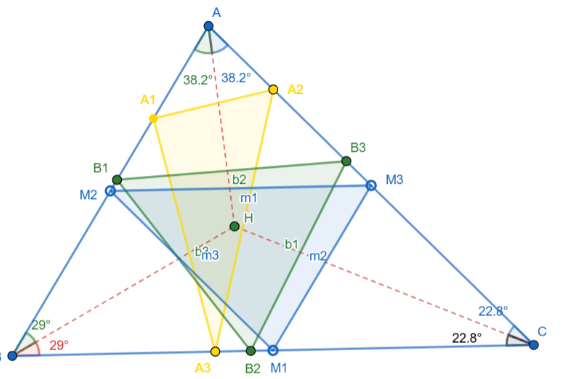
Steps in drawing from creating triangle through spotting points and joining segments, we create altitude respectively of each corresponding site. A, B and C we use vertex of these altitude to create triangle.

The median point must be rated A,B BC,AC we immediately create third triangle, combine also to show angles bisector equally and avoid repeating severally. In all these triangles get incorporated in one piece forming a beauty.

I have concluded my article effectively and would invite @solaymann @enamul17 @nancy0 @chant to join challenge