Why Bancor-like exchanges are expected to have fees, part 2

As the title suggests, this is a follow-up of our previous article “Why Bancor-like exchanges are expected to have fees”. There we showed that a Bancor-like exchange, defined as a contract that allows to:

1- Buy and sell shares: it accepts only tokens A or B to buy the share-token S.
2- Exchange the pair A / B.

must include a fee in order to attract investors. Without a fee any investor would be better outside the exchange. However we made a key assumption without explaining why it is valid to make it: “the amount of issued shares S is constant”. Here we will explain that this assumption can be removed, under a reasonable condition.

So now we want to describe all the possible states of our exchange in terms of a function S(x,y), where S is the number of share-tokens issued by the exchange (the exchange does not keep any tokens S for itself) in terms of x and y, the number of tokens A and B (respectively) inside the exchange. A crucial condition that we may impose to the function S is

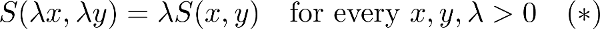
This condition can be expressed in words by saying that one token S is always backed and tradeable by the same amount of tokens A and B if we keep the ratio tokens A/tokens B constant. Or put it in other words, it means that we can split the exchange into two (or n) exactly equal exchanges with same state function S keeping all the prices untouched. Observe that exchanges following the Bancor algorithm satisfy this condition if and only if the sum of the fractional reserve ratios F ₁,…,F_m is 1. This can be seen directly from the formula

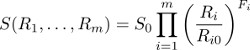
in Formulas for Bancor system. The condition F₁+...+F_m=1 holds for every existing exchange in Ethereum’s Bancor plataform, as far as we know, except for BNT/ETH.

The condition (*) implies that any particular investor does not care about other investors movements on the token S. The only variables that will affect the investor (still assuming no fees) would be the real world price movement of A and B and the shape of the curve S = constant.