An introduction to attribute logic aka first-order logic

background by @novaatebatman
Logic is the basic principle for mathematics and information technology, but it can be also used in political and philosophical argumentation. Many people like to say “that is logical” when they actually mean “that makes sense”... as someone who learned and likes how strict the concept of logic is, I would love if more people would stick to it's actual definition – I am usually no grammar nazi but this is important to me.
What is logic in the context of a debate?
The great thing about logical argumentation is that if you agree on the premises there is no way to deny the conclusion. Most of the time that leads to the insight that one of your premises must be wrong or at least needs some correction. A premise is a common value or definition that you and the people you are arguing with can agree on without further discussion. As a short example:
Premise 1: Every person should be free to do what they want!
Premise 2: Murderers should be in prison
Premise 3: You are not free when you are in prison
Premise 4: Murderers are people
Conclusion from 1+4: Murderers should be free
Conclusion form 2+3: Murderers should not be free
The most important rule in logic is that something can not be wrong and true at the same time. This is the very definition of a contradiction or what people like to call cognitive dissonance (I hate that word) . Which premise would you get rid of to solve the contradiction?

https://en.wikipedia.org/wiki/Wikipedia:Arguments_to_avoid_in_deletion_discussions
The language of first-order logic
I will skip talking about “the classic logic” to avoid confusion. First-order logic - we call it attribute logic in Germany - is more powerful than classic (p,q) logic. You have objects that are defined as small letters (a,b,c...) and capital letters with brackets showing their attributes (F(x), G(x), H(x)...), you also have some signs/vocabulary showing the relation of objects
„=“ means the objects are identical (not only equal in a mathematical way but the very same object)
„:=“ means you are defining a word or symbol
¬ := “not”
∧:= “and”
∨:= “or”
→:= conditional (“if..then...”)
↔:= biconditional (“only if... then..”)

http://inkfish.fieldofscience.com/2012/11/math-phobes-experience-arithmetic-like.html
I do use “and” and “or” instead of “∨” and “∧”. A quick example for the others:
a:= Tobi , F(x):=x is bored; “¬F(a)” then translates to “Tobi is not bored”
a:= Tobi , F(x):=x is bored, G(x):= x is on Steemit; “G(a)→¬F(a)” translates to “Tobi is not bored when he is on Steemit”
a:= Tobi , F(x):= x conquered the world , G(x):= x stops ; “G(a)↔F(a)” then translates to “Tobi will only stop if he conquered the world!”
Proofs
I will make some examples for logic proofs in future posts. Understanding the above and the basics of set theory is actually half a semester of logic. So do not worry if all this mathematical jibberish is a little overwhelming at first. Feel free to ask any questions in the comments. If you want to read thoughts about logic from important dead people than I recommend Hegel
Great post, followed.
Wow, great piece. But prefer logic in word rather than functions and maths... Well done dude
thx mate, the math can help to get "the unnecessary" parts of the language out of the way. It is bizarre at first, but it helps to truly focus on the logic of an argument.
Definitely, agree with you on that
I think that can be said about every grammar nazi :P
And I think you cognitive dissonance wrong.
mhhh It is just a fanzy word for having viewpoints that are contradicting, isn't it?
"the mental discomfort (psychological stress) experienced by a person who simultaneously holds two or more contradictory beliefs, ideas, or values."from wiki
it implies that mental discomfort thing, but that is bs imo.
There can be contradictions that do not cause mental discomfort.
dissonance is a possible subset of contradiction, but not all possibilities.
How would that look in logic notification? ;)
F(x):= x is a cognitive dissonance ; G(x):= x is a contradiction
F(x)->G(x) ,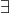.gif) x(¬F(x) und G(x))
x(¬F(x) und G(x))
I would normally describe it directly with subsets, but I wanted to stay with the vocabulary of the post.
Danke für den Resteem! :D
Nah I would actually need to describe it with a quantor like i did to put it into context of the rest of the argument
Great read indeed. Logic depends on how you see and understand it
thanks, but actually logic does not depend on how you see it, that is why i like it so much ;)
Good point, I agree. However some peple see logic in a diffrent way...however in reality, your view point is valid.
Dont forget to check out my post for a link to collect free crypto..a once in a life time opportunity.
Hi, thanks.
As this is not in the maths forum, can I add it to the math-list article coming up later today?
!-=o0o=-!
To follow curated math content follow @math-trail.
If you wish @math-trail to follow you then read this article.
Click here for Mathematics forum on chainBB
sure, buddy
Eine Off-Topic Frage: Mittlerweile ist es ja zwei Wochen her, dass du die Flyer verteilt hast. Hast du in der Zeit schon Leute gesehen, die geschrieben haben, dass sie wegen der Flyer hier seien oder aus deren Introduction-Posts du hättest schließen können, dass sie eventuell wegen deiner Flyer hier seien, z. B. anhand des angegebenen Wohnortes? :)