Ein chaotisches Wettervorhersagemodell im Insightmaker

Nach einer längeren Serie zu Causal Loop Diagrams (CLD) und systemischen Archetypen, möchte ich mich wieder Stock-Flow-Modellen zuwenden. Ich gehe davon aus, dass der Leser mit Stock-Flow-Modellen soweit bekannt ist, wie ich sie in meinen früheren Artikeln beschrieben habe, z.B. in Wie kann man aus Wirkungsnetzwerken simulationsfähige Stock-Flow-Modelle bauen.

In diesem und den darauf folgenden Artikeln habe ich gezeigt, wie man im kostenlosen Tool "insightmaker" ein Stock-Flow-Modell entwickelt.

Konvektionszellen

In Modelle können keine Emergenzen hervorsagen habe ich gezeigt, dass Stock-Flow-Diagramme nichts anderes sind, als numerisch gelöste Differentialgleichungen. Zudem habe ich dort auf das einfachste System am Rande zur Komplexität hingewiesen, nämlich eine von unten erwärmte Flüssigkeitsschicht, in der es zu der emergenten Bildung von Benardzellen kommt. Schauen Sie kurz in den Wikipediaartikel über den Bénard-Effekt, da ich hier nicht in der benötigten Tiefe darauf eingehe, um Personen, die noch nie davon gehört haben, auf den benötigten Stand zu bringen.

In diesem Artikel möchte ich dieses System mit einem Stock-Flow-Modell simulieren, um ein besseres Gefühl für solche Modelle zu erlangen. Zwar sind Stock-Flow-Diagramme von Jay W. Forrester zur Modellierung von sozialen und ökologischen Systemen erfunden worden und nicht als physikdidaktische Ergänzung gedacht. Dennoch ist es aus unten erwähnten Gründen erhellend, das sogenannte Lorenz-Modell einmal im insightmaker laufen zu lassen.

Um 1900 herum lieferte der Physiker Herni Bénard wichtige experimentelle Grundlagen zu Konvektionszellen in einer horizontalen Flüssigkeitsschicht, wie Sie z.B. in einer Pfanne bereitstellen, um Spaghetti zu kochen. Ab einer bestimmten Temperaturdifferenz zwischen der Heizplatte und der oberen Begrenzung der Flüssigkeit, kommt es zu bienenwabenartigen Konvektionszellen, wie ich sie im Artikel Modelle können keine Emergenzen hervorsagen abgebildet habe.

Das Lorenz-System

Der Meteorologe Edward N. Lorenz wollte ein aussagekräftiges Wettermodell entwickeln und besann sich auf die Arbeiten von Bénard, denn die Atmosphäre ist als Luftschicht mit einer Flüssigkeitsschicht vergleichbar. Auch bei der Atmosphäre herrscht zwischen der Erdoberfläche und einer wetterrelevanten Obergrenze eine Temperaturdifferenz.
Die rechnerische Behandlung der Bénardzellen, so wie sie Lorenz benötigte, ist ziemlich mühsam. Lorenz kam am Schluss auf drei Differenzialgleichungen, die direkt zu Beginn des Wikipedia-Artikels Lorenz-Attraktor stehen

X' = a(Y - X)
Y' = X(b - Z) - Y
Z' = XY - cZ

a, b und c sind irgendwelche Parameter. Die Ableitung von Z hängt u. a. vom Produkt von X und Y ab, daher ist diese Gleichung nicht linear, was eine rein mathematischen Behandlung ungemein erschweren würde.

Stattdessen wollen wir diese drei Gleichungen in einem Stock-Flow-Diagramm modellieren. X, Y und Z sind die Bestände, ihre Ableitungen die Flüsse. Das ist immer so: Flüsse sind Veränderungen der Bestände, also ihre Ableitungen. Umgekehrt sind Bestände die aufsummierten Flussbeiträge, also die Integrale. Das zeigt, dass alles ein Bestand sein kann, je nachdem, wofür wir uns interessieren. Z.B. ist die Variable X proportional zur Konvektionsgeschwindigkeit, wie Andreas Jung in Lorenz-System und seltsame Attraktoren beschreibt

Klassische Systemdynamiker, die herausstreichen, dass Bestände nur solche Variablen sein können, die sich nicht ändern, wenn die Zeit angehalten würde, hätten wohl Mühe, eine Konvektionsgeschwindigkeit als Bestand zu akzeptieren. Das kommt daher, weil Geschwindigkeiten gemeinhin mit einer zeitlichen Veränderung (des Ortes) assoziiert werden. Betrachten wir eine Geschwindigkeit aber als Integral der Beschleunigung, dann wird es klar, dass auch eine Geschwindigkeit ein Bestand sein kann.

Das Modell im Insightmaker

Wir müssen im insightmaker also drei Bestände zeichnen, die wir natürlich ebenfalls mit X, Y und Z bezeichnen. In jeden Bestand führt ein Fluss, der durch eine der drei Gleichungen definiert ist. Beispielsweise führt in den Bestand X der Fluss a(Y - X), d.h. er hängt von den Beständen X und Y sowie von einem Parameter a ab. Wir zeichnen also einen Link von X zu seinem Fluss, von Y zu diesem Fluss und von einer Variablen a zu diesem Fluss. Die Gleichung für den Fluss schreiben wir in das Feld "Flow Rate". Schauen Sie sich das Modell hier an: Lorenz im Insightmaker! Wie immer, können Sie es kopieren und selber damit herumspielen. Weil ich weiss, dass es trotz dieser Aufforderung immer wieder Leser gibt, die nicht in eine andere Website hinein klicken mögen, bilde ich das fertige Modell hier ab:

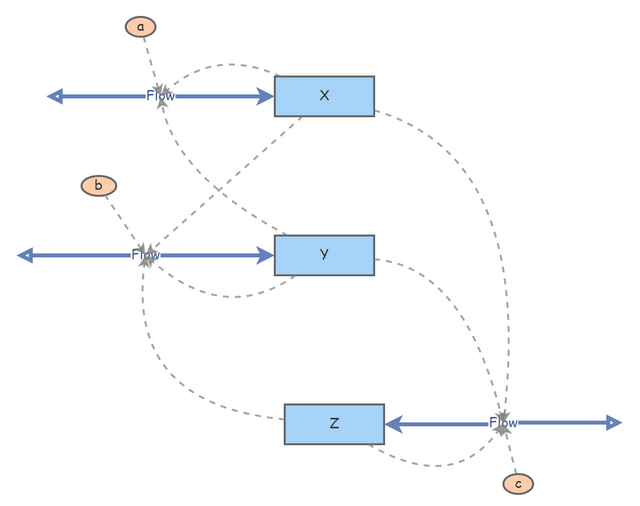
Beachten Sie, dass der Fluss a(Y - X) auch mal negativ werden kann, nämlich dann, wenn X > Y ist. Unterhalb des Feldes "Flow Rate" ist das Feld "Only Positive Rates", was standardmässig mit "Yes" belegt ist. Das müssen Sie unbedingt in "No" ändern! Das bedeutet anschaulich, dass der Fluss nicht nur in den Bestand hineinfliesst, sondern zuweilen auch aus dem Bestand abfliessen kann. Man sagt, dass es sich um einen Nettofluss handelt. Sie könnten die Gleichung auch so modellieren:

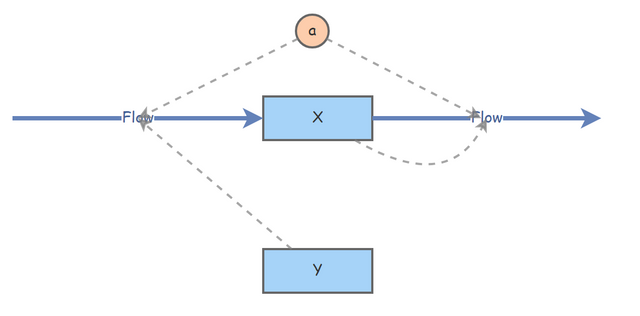
Der Inflow hat die Flow Rate aY, der Outflow aX (nicht etwa -aX). Allerdings ist diese Darstellungsart auch nicht sehr spezifisch, denn Y könnte ja negativ sein, dann würde der "Inflow" doch zu einem Outflow, denn auch in dieser Darstellungsart können wir nicht garantieren, dass die Raten stets positiv sind.

Weil die Flüsse immer sowohl hinein als auch heraus fliessen können, werden dann auch die Bestände nicht immer positiv bleiben. Für die Konvektionsgeschwindigkeit bedeutet das z.B., dass die Konvektion sowohl nach rechts als auch nach links drehen kann. Deshalb müssen Sie bei den Beständen das Feld "Allow Negatives" auf "Yes" setzen.
Nun zu den Anfangsbedingungen: Würden alle drei Bestände am Anfang schon verschwinden, hätten also den Wert 0, dann würde nichts passieren. Die Bestände würden auf ewige Zeiten den Wert 0 behalten. Also müssen Sie den Beständen einen von 0 verschiedenen Anfangswert geben. Ich habe ihn bei allen drei auf 0.01 gesetzt, also fast 0.

Haben Sie alle drei Gleichungen eingegeben, können Sie die Simulation starten. Allerdings muss ich hier noch eine wichtige Bemerkung machen. Es gibt in der Mathematik Gleichungen, die sehr instabil sind, d.h. je nach Berechnungsmethode resultieren immer andere Ergebnisse oder es kommt gar Unsinn heraus. Hier ist es ähnlich. Wenn Sie nicht aufpassen, nimmt vor allem Z riesige Werte an, die insightmaker nicht mehr rechnen kann. Wählen Sie deshalb in den "Settings" den "Analysis Algorithm Accurate (RK4)" und den "Time Step 0.01" aus.

Attraktoren

Nun werden Sie - je nach Werte, die Sie den Variablen a, b und c zugeordnet haben - zwei verschiedene Verhalten beobachten. Das eine sieht so aus:

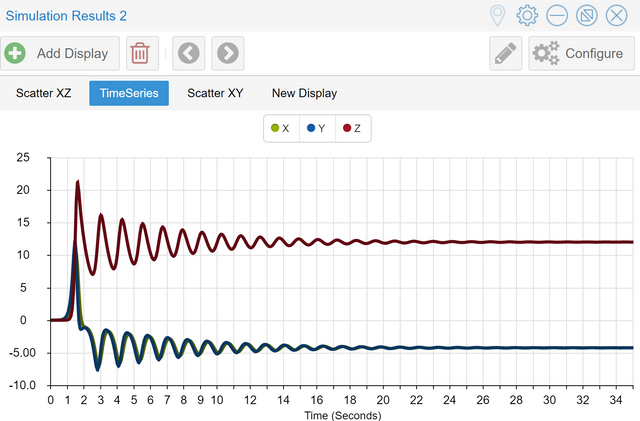
Hier entwickeln sich die Bestände auf einen einzigen Wert hin. Man spricht von einem Punktattraktor.
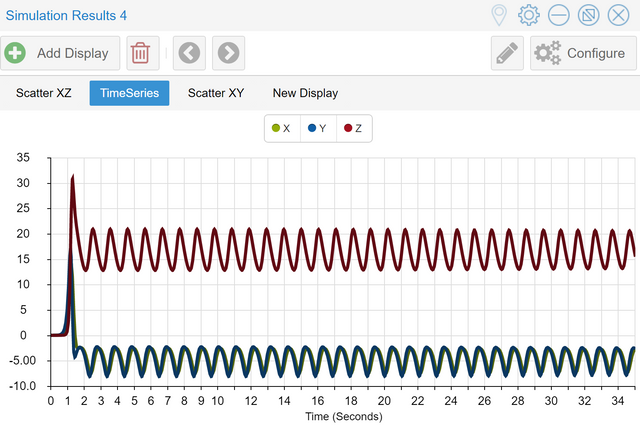
Das andere Verhaltensmuster sieht in der Zeitreihe so aus:

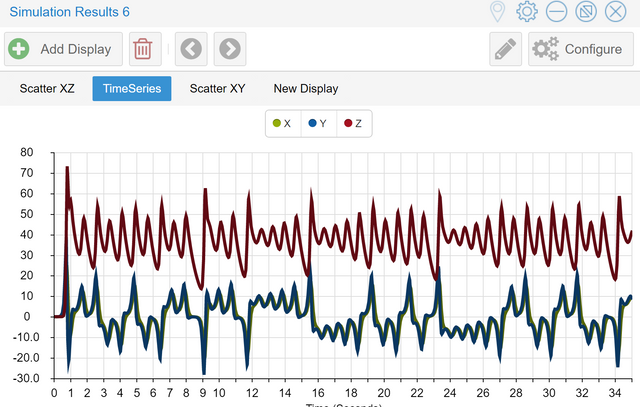
Das scheint eher chaotisch. Die Ausschläge der Kurven sind immer anders. Wenn Sie im Simulationsfenster auf "Add Display" klicken und dann "Scatter Plott" wählen, können Sie zwei der drei Bestände auswählen, z.B. X und Y. Das Display zeigt dann nicht die Abhängigkeit der Bestände von der Zeit, sondern ihre gegenseitige Abhängigkeit. Sie werden sehen, dass diese Plots ziemlich nahe an den bekannten Lorenz-Attraktor mit seinem schmetterlingshaften Aussehen kommen. Hier ist er also, der berühmte Lorenz-Attraktor!

Als typische Werte für einen "schönen" Attraktor werden die Werte a = 10, b = 28 und c = 8/3 empfohlen. Experimentieren Sie auch mit anderen Werten. Sie können mein Modell nehmen, es klonen und dann den Variablen selber Werte zuordnen.

System Dynamics ist nicht für physikalische Systeme geeignet

Zwischen dem Punkt- und dem Lorenzattraktor gäbe es noch den sogenannten Grenzzyklus. Hier oszillieren die Bestände zwischen zwei Extremwerten hin und her, z.B. so:

Durch Variation des Parameters b sollte auch dieser Zustand erreicht werden können. Andreas Jung macht in Lorenz-System und seltsame Attraktoren folgende Angaben:

Für b<13.926 hat man Punktattraktoren.
Für 13.926<b<24.74 hat man Grenzzyklen.
Für b>24.74 hat man einen seltsamen Attraktor, d.h. das System ist chaotisch.

In meiner Darstellung Lorenz im Insightmaker sind diese Grenzen nicht so einfach nachvollziehbar. Je nachdem, wie fein ich in den Settings die "Simulation Time Step" mache, weist das System ein anderes Verhalten auf. Insbesondere kann ich Grenzzyklen nie beobachten, d.h. ab einer gewissen Zeit - z.B. ab t=150 - kollabieren sie entweder zu einem Punkt oder werden immer grösser und kippen in einen seltsamen Attraktor. Ungefähr bei b=18.42 scheint bei mir diese Grenze zu sein. Das Problem ist, dass ich bei sehr kleinen Simulation Time Steps in der Zeit kaum vorwärts komme und deshalb für die "Simulation Length" nicht über 50 gehen kann, sonst sitze ich "ewig" vor dem Bildschirm.

Um bessere exerimentelle Resultate zu bekommen, muss man sich anderer Simulationstools bedienen. Das zeigt, dass System Dynamics nicht zur Simulation von physikalischen Systemen geeignet ist. In sozialen und ökologischen Systemen geht es ja auch nicht darum, den genauen Wert eines Kontrollparameteres zu finden, bei dem das System eine Verhaltensverzweigung aufweist.

Komplex heisst chaotisch

Noch eine Bemerkung zum Begriff "chaotisch": ein System entwickelt sich entweder auf einen Punkt oder ein Oval hin. Im ersten Fall kommt seine Dynamik zum Erliegen, im zweiten Fall pendelt sie "gleichmässig hin und her" (Oszillation).
Dann gibt es noch einen dritten Fall, wo die Entwicklungslinie des Systems zwar in einem bestimmten Gebiet verbleibt, d.h. die Werte aller Parameter variieren innerhalb eines endlichen Intervalls, aber schneidet sich nie selber. Das ist der Fall, wenn die Entwicklungslinie "unendlich verschlungen" ist, was mindestens drei Bestände benötigt. Dieses Enwicklungsmuster nennt man "seltsamen Attraktor" und wird gewöhnlich mit "chaotisch" umschrieben. Ein komplexes System ist stets chaotisch! Gewisse Denkansätze, wie z.B. das Cynefin-Modell, glauben, dass es komplizierte, komplexe und chaotische Systeme gibt. In der Komplexitätsforschung ist diese Unterscheidung nicht möglich. Soziale Systeme sind komplexe Systeme und entwickeln sich auf einem seltsamen Attraktor, sind also nicht vorhersehbar, ungewiss, emergent. Deshalb sind sie als chaotisch zu bezeichnen.