Die Anatomie eines Causal Loop Diagrams
Natürlich weiss ich, dass meine Gedanken auf Steemit nicht gerade das kollektiven Bedürfnis spiegeln. Aber irgendwo muss ich sie niederschreiben. Und nachdem ich mit meinem Blog hierher umgezogen bin, muss Steemit meine Aufsätze eben aushalten. Im folgenden möchte ich dem Wesen von Causal Loop Diagrams (CLD) auf den Grund gehen. Wahrscheinlich interessiert das hier "kein Schwein". Ich schreibe es mehr für mich und zum Verlinken nieder.
Ein Loop kann auf zwei Parameter vereinfacht werden
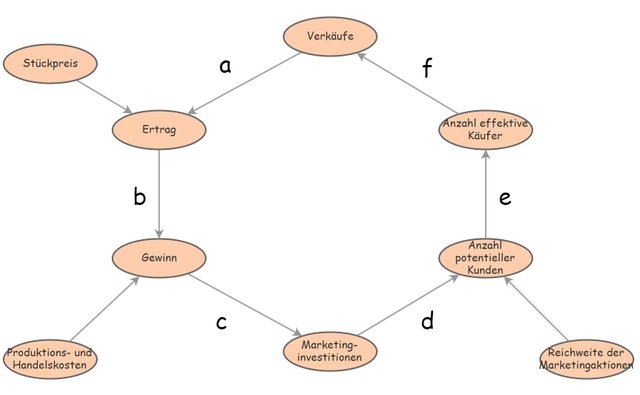
Wir haben beim Studium der Archetypen festgestellt, dass die Parameter in einem Feedbackloop ziemlich willkürlich sind. Ein häufig auftretender Feedbackloop war die gegenseitige Abhängigkeit der Verkäufe und den verkaufsfördernden Massnahmen der Marketininvestitionen. Je mehr Verkäufe in einer Periode stattfinden, desto höher der Ertrag, der sich als Produkt aus der Anzahl Verkäufe und des Stückpreises berechnet.
Den Stückpreis können wir als (temporäre) Konstante betrachten und "in den Ertragsparameter hineinnehmen". Der Gewinn ist die Differenz zwischen dem Ertrag und den Produktions- und Handelskosten. Auch diese können wir als (temporäre) Konstante ansehen. Vom Gewinn können wir einen Teil in Marketingaktionen investieren. Wie gross dieser Teil ist, hängt davon ab, was das Unternehmen sonst noch für Projekte und Verpflichtungen hat. Das weisen wir hier auch nicht separat aus, sondern gehen davon aus, dass der Anteil für Marketing ein gewisser konstanter Prozentsatz des Gewinns beträgt. Je nach Reichweite der Marketingaktionen genereieren diese eine Menge an potentiellen neuen Kunden. Solange wir uns nicht eingehender mit den Ursachen der Reichweite beschäftigen, nehmen wir auch hier eine konstante Reichweite an. Mit demselben Argument wie oben können wir die Reichweitenkonstante auch gleich in die Definition des Parameters "Anteil potentieller Kunden" hinein denken. Schliesslich wird ein gewisser Anteil der potentiellen Kunden zu effektiven Käufern.
(Für diejenigen, die sich mit Hompotopietehorie auskennen: wir ziehen nullhomotope Bereiche des CLD zusammen, so dass nur noch die Kreise im CLD übrigbleiben).
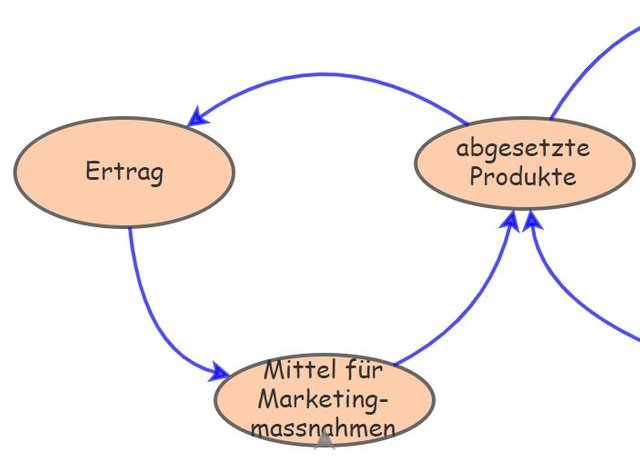
Diesen Feedbackloop haben wir in den verschiedenen Archetypen immer etwas anders dargestellt. In Hat Ihr Fahrzeug auch eine Bremse, um die Bremse zu bremsen? sah er so aus:
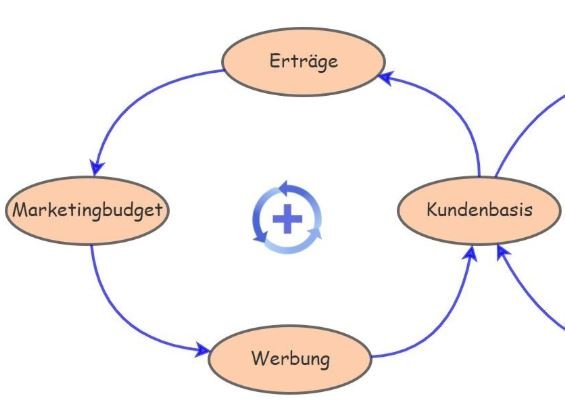
und in Die Schwierigkeiten wachsen, je näher man dem Ziel kommt so:
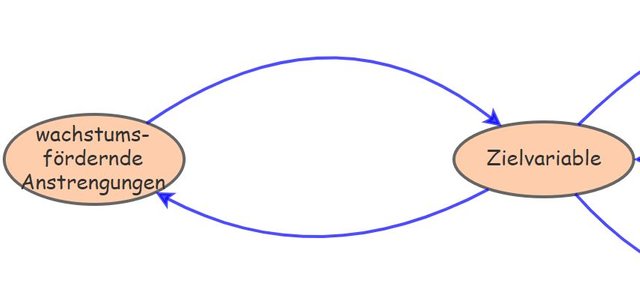
In Was macht die Attraktivität eines Produkts aus? ist der Feedbackloop zu folgendem abstrahiert:
Die Zielvariable würde wohl am besten mit der Anzahl Verkäufe und die "wachstumsfördernden Massnahmen" mit den Marketinginvestitionen identifiziert, so dass unser ursprünglicher Feedbackloop eigentlich nur aus zwei Parametern besteht:
Der Pfeil "Verkäufe --> Marketininvestitionen" ist die Zusammensetzung zwischen den Pfeilen a, b und c in der ersten Figur dieses Artikels. Der Rückpfeil "Marketinginvestitionen --> Verkäufe" ist dagegen die Zusammensetung der Pfeile d, e und f. Natürlich ist eine solche "Kurzversion" des Causal Loop Diagrams nicht sonderlich verständlich, aber korrekt und für Insider ausführlich genug.
Wie sind die beiden gegenläufigen Pfeile zu verstehen?
Um das zu verstehen, machen wir ein Beispiel. Wir denken uns einmal konkrete Funktionsbeziehungen zwischen den einzelnen Parametern des Feedbackloops aus, um zu sehen, was passiert. Natürlich macht man das auf der Ebene der Causal Loop Diagrams nie. Solche quantitativen Überlegungen sind den Stock-Flow-Modellen überlassen. Aber wir wollen einmal so tun, als wären wir im Begriff, aus dem vorliegenden Feedbackloop ein Stock-Flow-Diagram zu modellieren und überlegten uns schon mal mögliche Funktionsgleichungen.
In der ersten Figur könnte gelten:
a) Ertrag = Stückpreis * Verkäufe, also z.B. Ertrag = 10*Verkäufe, wenn wir für den Verkauf einer Einheit 10 Euro einnehmen.
b) Gewinn = Ertrag - Kosten, also z.B. Gewinn = Ertrag - 5*Verkäufe, wenn wir zur Produktion und Verkauf einer Einheit 5 Euro aufwenden müssen.
c) Wenn wir z.B. 10 % des Gewinns in Marketing investieren, also z.B: Marketinginvestitionen = 0.1*Gewinn.
Zusammengesetzt ergibt sich der Pfeil "Verkäufe --> Marketinginvestitionen" zu
Marketininvestitionen = 0.1 * (10 * Verkäufe - 5 * Verkäufe) = 0.5*Verkäufe (1)
Die 0.5 sind Euro/Einheit, die Verkäufe werden in Einheiten gemessen.
Rückwärts könnte es so aussehen:
d) Anzahl potentieller Kunden = Reichweite * Marketininvestitionen, z.B. wenn wir pro Euro zehn potentielle Kunden erreichen: Anzahl potentieller Kunden = 10 * Marketinginvestitionen
e) Anzahl effektive Käufer = 5 % der potentiellen Kunden, also
Anzahl effektive Käufer = 0.05 * potentielle Kunden
f) Schlieslich gilt Verkäufe = Anzahl Einheiten pro Kunde * Anzahl effektive Kunden, also z.B.
Verkäufe = 6 * Anzahl effektive Kunden, wenn jeder Kunde im Schnitt 6 Einheiten bestellt, z.B. 6 Äpfel pro Woche.
Zusammengesetzt erhalten wir
Verkäufe = 6 * 0.05 * 10 * Marketinginvestitionen = 3 * Marketininvestionen.
Würden wir die Marketinginvestitionen durch die Gleichung (1) ersetzen, erhielten wir
Verkäufe = 1.5 Verkäufe, oder 1 = 1.5, was ein Widerspruch ist. Was ist geschehen?
"Verkäufe" sind eben nicht "Verkäufe"! Die Verkäufe links des Gleichheitszeichens sind Anzahl Geschäftstransaktionen in der aktuellen Zeitperiode, während die Verkäufe rechts des Gleichheitszeichens die Anzahl Geschäftstransaktionen der vergangenen Zeitperiode bezeichnen. Das heisst dann also: In jeder Zeitperiode gibt es 1.5 Mal mehr Geschäftstransaktionen als in der Zeitperiode davor. Und das macht Sinn.
Der Zeitturm
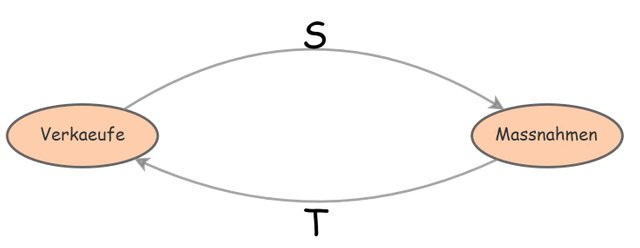
Mit einem Feedbackloop, den wie in seiner einfachsten Darstellungsart so hinzeichnen,
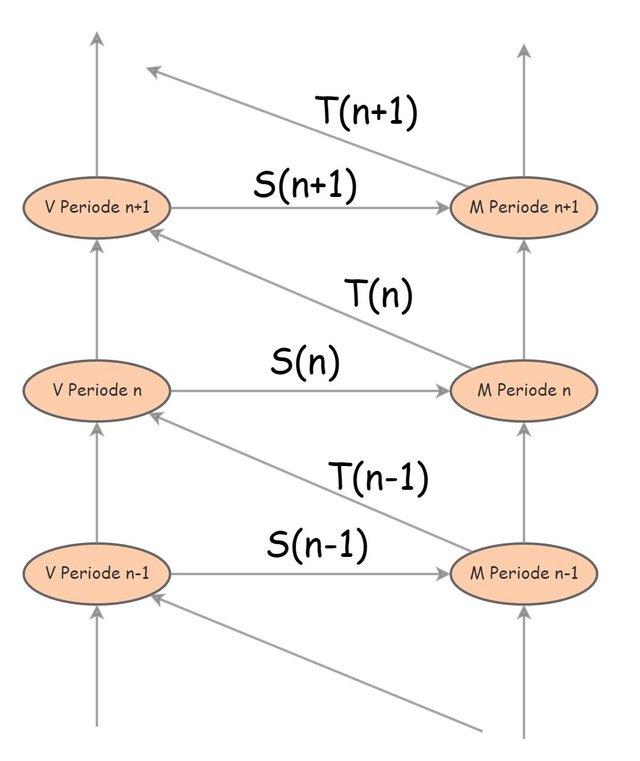
meinen wir eigentlich einen "Turm" von Verkäufen und Massnahmen. Jedes "Stockwerk" markiert dabei eine Zeitperiode, die durch n nummeriert wird. V bezeichnet die Verkäufe, M die Massnahmen, die in diesem Fall Marketinginvestitionen sind.
Die senkrechten Pfeile kommen jeweils durch die geeignete Zusammensetzung von S und T zustande. Durch Anwendung der Assoziativität von Funktionen zeigt man, dass das Diagramm kommutiert.
Weitergehende Katalogisierung der Komponenten eines CLD
Die Parameter - hier "Verkäufe" und "Massnahmen" - sind durch die Menge der natürlichen Zahlen realisiert. Im allgemeinen sind es Teilordnungen, sogenannte Posets. Sie lassen sich durch die Festlegung, dass wenn die natürliche Zahl i kleiner oder gleich der natürlichen Zahl k ist, dass dann ein Pfeil i --> k existiert, zu einer kleinen Kategorie machen. Zwischen zwei Objekten gibt es also höchstens einen Pfeil. Die Abbildungen S und T werden dann zu Funktoren zwischen den beiden Posets V und M. In unserem Beispiel sind die beiden Pfeile monotone Abbildungen. Ist einer der beiden Funktoren, z.B. T: M --> V, eine antitone Abbildung, dann wird der entsprechende kontravariante Funktor T: M --> V, der von der dualen Kategorie M* ausgeht, wieder zu einer monotonen Abbildung. Die duale Kategorie M* erhält man, indem man in der Kategorie M die Pfeile umkehrt. Im Poset der natürlichen Zahlen heisst das, dass man aus "kleiner gleich" einfach die Relation "grösser gleich" betrachtet.
Warum sind V und M mit der Menge der natürlichen Zahlen gleichzusetzen? Die Verkäufe geben die Anzahl verkaufter Einheiten an. Das ist immer eine natürliche Zahl. Sie haben in dieser Woche vielleicht 257 Einheiten verkauft.
Die Massnahmen sind Marketinginvestitionen in Geldeinheiten. Messen Sie diese in Hundertstel Geldeinheiten, z.B. Cents. Falls Sie doch noch an einer Kommastelle interessiert sind, messen Sie die Marketinginvestitionen halt eben in Tausendstel Euros oder meinetwegen in Vietnamamesischen Dongs. Sie können stets erreichen, dass Sie die Marketinginvestitionen als natürliche Zahl angeben können!
Wenn Sie z.B. einen Parameter "Motivation" haben, dann denken Sie sich, dass sie zwischen 0 ("kein Bock") und 1 ("hochmotiviert") liegt. Auch da genügt es, wenn Sie den Parameter auf 2 Kommastellen genau angeben. Das entspricht aber dann genau den natürlichen Zahlen zwischen 0 und 100.
Ein anderer Einwand könnte sein, dass die Zeit nicht diskret ist. In der Praxis ist sie es auf jeden Fall! Verkäufe werden stets pro Periode gemessen, rapportiert und "geforecastet". Ein System Dynamics Stock-and-Flow-Modell hat stets eine endliche Schrittgrösse. Insightmaker gibt standardmässig eine Schrittgrösse von 1 vor und rechnet mit dem Näherungsalgorithmus nach Euler. Unterteilen Sie die Schrittgrösse in 100 oder 1000 Zeiteinheiten und schalten das Runge-Kuttaverfahren ein, überfordert das den Computer und er bleibt fast stehen. Gewonnen haben Sie meist wenig. Euler mit Schrittgrösse 1 oder allenfalls 0.1 ist genau genug, um die Prognosen zu machen, die Sie interessieren. Wenn Sie also beispielsweise ein stetig verzinstes Kapital simulieren, dann spielt es keine Rolle, ob Sie mit einer Zinsperiode von einem Jahr oder von einem Tag rechnen. Die Differenzen, die Sie erhalten, sind für die Diskussion des Systems nicht relevant.
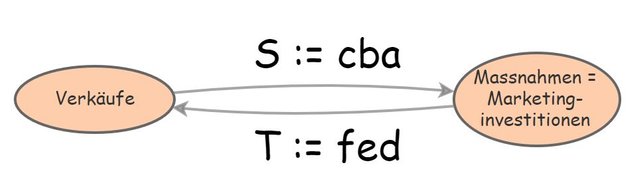
Im ersten Diagramm muss aber noch berücksichtigt werden, dass diese Loops nicht "ewig" zirkulieren, sondern dass es gegenläufige bzw. bremsende Faktoren gibt, z.b:
Durch diese Bremsungseffekte sind aber auch Deine Zahlenspiele reine Theorie. Leider sind diese unrealistischen Modelle auch ein Grund, warum in der Wirtschaft immer noch vom endlosen Wachstum geträumt wird...
Nein, @stayoutoftherz! Da ist jetzt genau das passiert, was ich befürchtet habe: das er von Lesern missverstanden wird, die die vorherigen Artikeln nicht gelesen haben. Der Artikel baut natürlich auf den vorhergehenden auf. Die Bremseffekte werden z.B. durch die Archetypen "Grenzen des Wachstums", "Growth and Underinvestment" oder durch das Attraktivitätsprinzip beschrieben, wie ich sie in den früheren Artikeln vorgestellt habe. Ich glaube, ich habe zu Genügen dargestellt, dass es endloses Wachstum nie gibt.
Zudem muss der Leser des aktuellen Artikels wissen, was Stock-and-Flow-Modelle sind und wie man sie entwickelt, um zu wissen, dass es in meinen Zahlenbeispiele bestimmt nicht um eine möglichst realistische Modellierung geht, sondern darum, ein CLD als mathematisches Objekt zu verstehen. Die Zahlenbeispiele sollen zeigen, wie die beiden gegenläufigen Pfeile zueinander stehen. Der Leser soll verstehen, dass es nicht etwa inverse Funktionen sind und dass der eine Pfeil Posets derselben Zeitperiode abbildet, während der andere ein Shift in die nächste Zeitperiode darstellt. Und dass diese Charakterisierung völlig unabhängig von Beständen und Flüssen ist. Dazu muss der Leser halt auch die laufenden DIskussionen über CLD kennen, die in der System Dynamics Community geführt werden und auf die ich in früheren Artikeln hingewiesen habe.
Dann schreibe doch einfach dazu, dass zum korrekten Verständnis die vorherigen Artikel gelesen werden müssen und die laufenden DIskussionen über CLD gekannt werden müssen, um Mißverständnisse zu vermeiden. Das war nicht ersichtlich.
Danach sollte man sein Blog-verhalten ja auch nicht unbedingt ausrichten. ;-)
Genau! Das ist auch meine Meinung. 😁
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!