Mathematics × Programming Competition #7 - Geometrical solution
This is my solution to @kenchung contest #7:
https://steemit.com/contest/@kenchung/question-mathematics-programming-competition-7
Question
A point is chosen randomly in a square. 4 lines are drawn to connect this point with the 4 vertices of this square, such that 4 triangles are formed. Find the probability that all interior angles of the 4 triangles are less than 120°. Give your answer correct to the nearest 3 decimal places.
Geometrical solution
First of all, let's consider a square. For simplicity, we are going to choose a square with side equal to 1, that also has an area of 1.
If we choose randomly a point inside the square, and draw the triangles from it, what are the angles of those triangles?
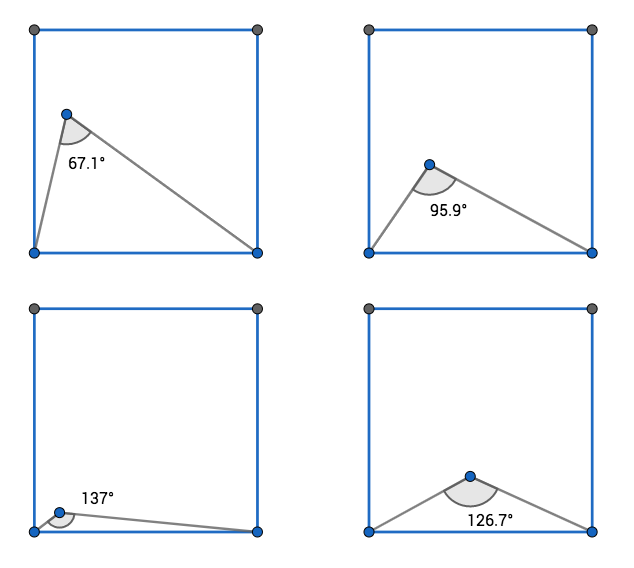
We can consider just one of the triangles for now, the reasoning for the other 3 triangles are the same due to the symmetry of the figures.
As you can see, the angles at the base of the triangle are never going to be more than 90°, because the random point P is inside the square.
So the only angle that could be more than 120° is the angle on P.
I will solve this problem by first finding out all the possible cases when the angle is 120° or more.
To find all the points that give an angle of 120° we can consider AB to be a chord of a circle such that the inscribed angle is 120°
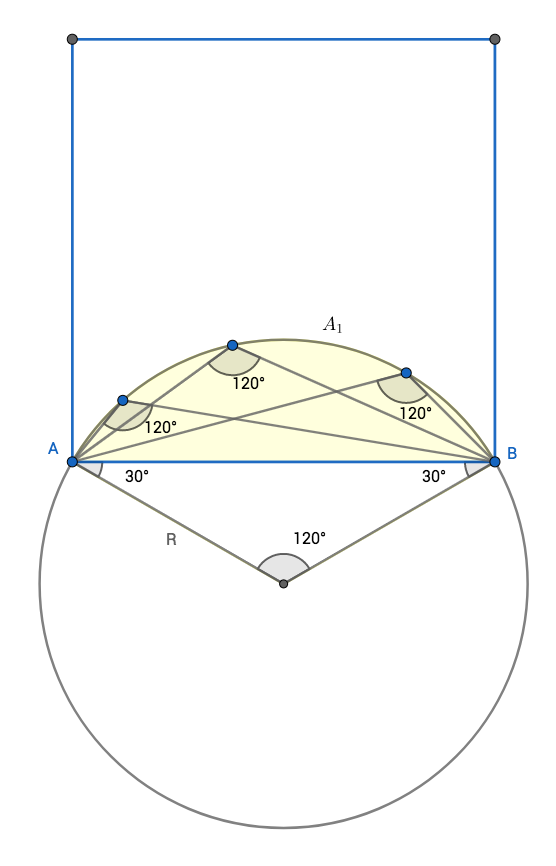
Now, all the points inside that circular segment are the points that gives as an angle of at least 120°.
If we do that same for the 4 sides of the square, we can see that the points that gives at least one angle greater than 120° are in the union of 4 circular segments.
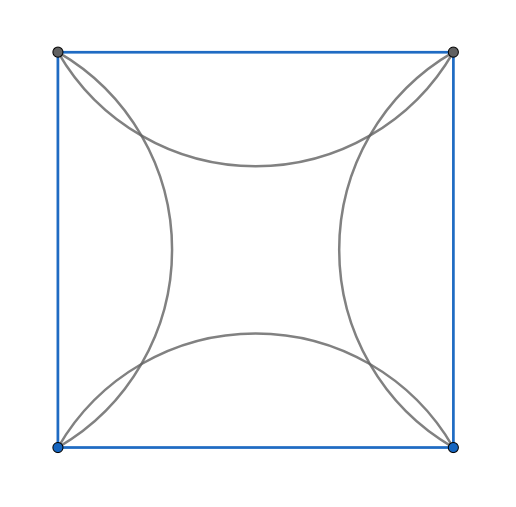
Only choosing a point not in the circular segments gives us angles less than 120°.
Therefore the area of the square minus the areas of the union of circular segments is the solution to our problem. (Because we choose a square with area 1, otherwise the probability would be the ratio of that area and the total area of the square)
Finding the area of the circular segment
First, let's find the radius R of the circle.
Using the law of sines:
AB / sin(120°) = R / sin(30°)
AB = 1
R = sin(30°) / sin(120°) = 1/2 * 2/√3 = 1/√3
Now, we can compute the area of the circular segment
(https://en.wikipedia.org/wiki/Circular_segment)
A1 = R^2 / 2 (120°/180°*π - sin(120°))
= 1/6 (2/3π - √3/2)
= 1/9 π - √3/12
Area of the intersection of the circular segments
Now we have to be careful, because if we sum the 4 areas of the circular segments we are going to have some area counted twice. Therefore we have to find the areas shown in the figure:
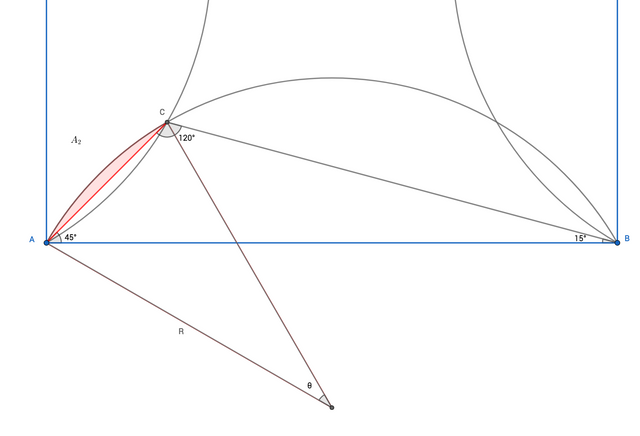
That is another circular segment!
Let's find the length of AC and the angle θ:
AC / sin(15°) = AB / sin(120°)
AC = sin(15°) / sin(120°) = (√6 - √2)/4 * 2/√3
Again, with the help of wikipedia (https://en.wikipedia.org/wiki/Circular_segment)
AC = 2R * sin(θ/2)
sin(θ/2) = AC / 2R
θ = 2 arcsin(AC/2R)
θ = 2 arcsin((√6 - √2)/4 * 2/√3 * √3/2)
θ = 2 arcsin((√6 - √2)/4)
θ = 2 * 15°
θ = 30°
Now, the area of the circular segment is:
A2 = R^2 / 2 (30°/180°*π - sin(30°))
= 1/6 (1/6π - 1/2)
= 1/36 π - 1/12
Conclusion
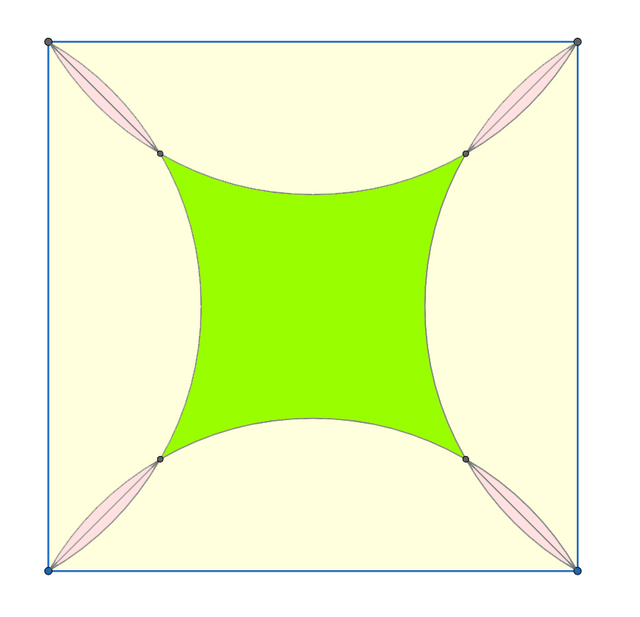
The total area of the union of the 4 circular segments is:
A = 4 * A1 - 8 * A2
= 4(1/9 π - √3/12) - 8(1/36 π - 1/12)
= 0.787
The answer to the question is then
Probability = 1 - A = 0.213

Didn't know the cat was that good with math
Great work! I can confirm that your answer is correct :)
I will announce the winners in a few days, hope that you will be one of the winners! :)
The diagrams are very professional.
I like the diagrams!!!
(I think I got the same solution :) )
How I tried to solve the problem.

@armandocat got you a $8.31 @minnowbooster upgoat, nice! (Image: pixabay.com)
Want a boost? Click here to read more! @originalworks
The @OriginalWorks bot has determined this post by @armandocat to be original material and upvoted it!
To call @OriginalWorks, simply reply to any post with @originalworks or !originalworks in your message!
To enter this post into the daily RESTEEM contest, upvote this comment! The user with the most upvotes on their @OriginalWorks comment will win!
For more information, Click Here!
Special thanks to @reggaemuffin for being a supporter! Vote him as a witness to help make Steemit a better place!
Great work!
Your diagrams are very professional.
I want to consult a question.
What soft do you draw the diagrams?
Thanks!
The tool is:
https://www.geogebra.org
It's very nice!
Thank you!
It is really very nice. I will try it!
And the programming?
Aaaaahhhhhh! I wrote some code to solve this but stupidly forgot to check the fourth triangle because it needed slightly different treatment.
Thanks for posting your solution, it all makes sense now :)
What is the secret that you joined this platform recently and you are reaping big?I however like your post.Follow me back.