Python 繪製星球軌道教學(1)——讓一顆星球繞恆星走
太陽系示意圖(圖片來自圖庫)
在開始之前,你需要的先備智識:
- Python 基礎語法(基本I/O、迴圈等)
- 初中數學及一點向量智識(有概念即可)
你將可以在此學到 :
- 如何繪製單顆星球繞恆星運轉
- 何謂數值分析
- 微積分的概念
前言
理查‧費曼(Richard Feymann)在加州理工大學擔任教職之際,出版《費曼物理學講義》(網路上也有電子中文版,請自行搜索),書籍分述不同物理領域智識,一共三卷。希冀藉由此書出版,給予大一、大二學生清楚的觀念。
而在第一卷第九章第七節〈行星運動〉中,他曾談到行星軌道的計算:
對於吊掛在彈簧上的物體所做的震盪運動來說,以上的分析(數值分析)顯然不錯。那麼我們是否可以用類似的方法來分析行星繞太陽的運動呢?我們想知道是否可以用這個方法來得到一個近似橢圓的軌道?為了簡化問題,我們將忽略太陽本身的運動。假設一行星自某位置出發,以某一速度向前進,它沿某條曲線繞著太陽運動:我們將利用牛頓的運動定律及重力定律來分析此行星的運動,希望了解其軌跡為何。——《費曼物理學講義》
這便是此系列的主題,我們要結合物理、數學及程式來玩轉星球軌道模擬,一步步實作,探討當中的數學理論並知其物理原理,進而能模擬星球繞行恆星。
由於自身常使用 Python 撰寫程式,知道其相當好上手,不需要定義太多東西,能捨去繁瑣的語法,專注在代碼的編寫上,代碼也很容易讀;而且網路上的教學資源也蠻多,可以自己學完基礎後再來讀這教學,沒有太特別的語法與邏輯,學習曲線不會太陡,不需耗費太多心力銜接。所以在此系列,我將使用 Python 作為程式編撰的語言。
他人也可以自行用其他語言寫代碼,歡迎眾人分享自己寫的版本。而要是在學習、安裝 Python 中有問題的話,可以將問題截圖或詳細描述問題放在留言上,我會盡可能去解決你們的問題。
物理分析與推導
在此我直接講述整個推導過程,若想要更詳細的介紹就直接參閱《費曼物理學講義》的內容吧!
我們先處理二維空間上的行星繞恆星模擬,再推導到三維空間上。費曼利用一張圖(9-5,因版權問題不直接上傳)來說明星球受到的力,將力分成 Fx 和 Fy 兩道,利用相似三角形的方法,我們可以推導出下列式子:
接著使用最原始的 F = ma,進一步得到下列方程式:
依此類推,Y分量也可以推導出同等關係:
在此我們假定 GM≡1,於這種單純的一顆星球繞行恆星的情況下,只需知相對距離就好,兩者的質量不是很重要。
設定好一些參數後,我們便可以利用數值分析來模擬行星運行。但有一個參數跟數值分析息息相關,所以在編寫之前,我們還需要了解數值分析的概念才好實作。
何謂數值分析
數值分析(numerical analysis)簡而言之就是利用電腦解決一些問題。雖然不能完全搓合答案,但可以非常近似所要的解。
以這系列為例,我們會將橢圓曲線離散化,分割成有限的點,計算每個時間點星球的位置、速度、加速度。要計算這些變化,其概念就像微分一樣:
而我們的計算流程如下(記得 ϵ 是時間間隔):
時間是種連續的東西,無時無刻都在改變,時間可以不斷分割,但如此一來,資料量必然是無限。所以我們只能用一小段時間作為基本單位,將其限制在有限,改變量也隨著最小單位時間來變化。
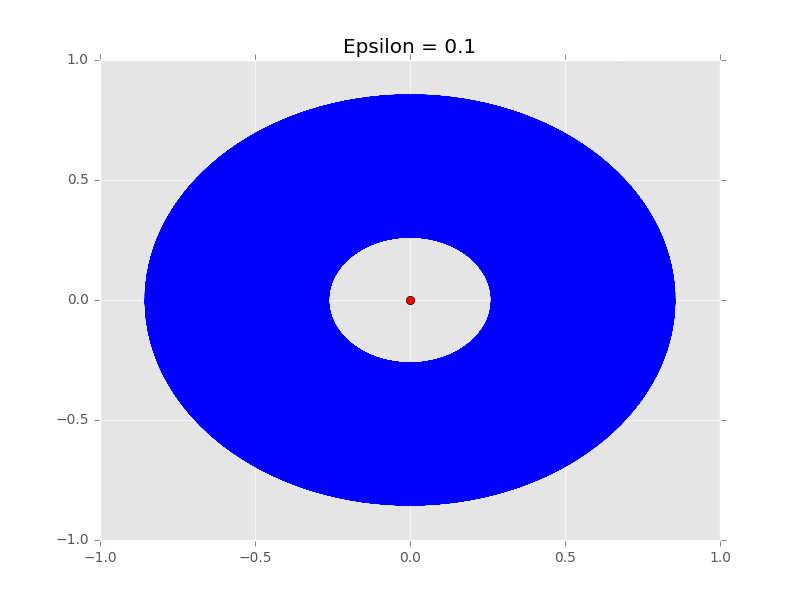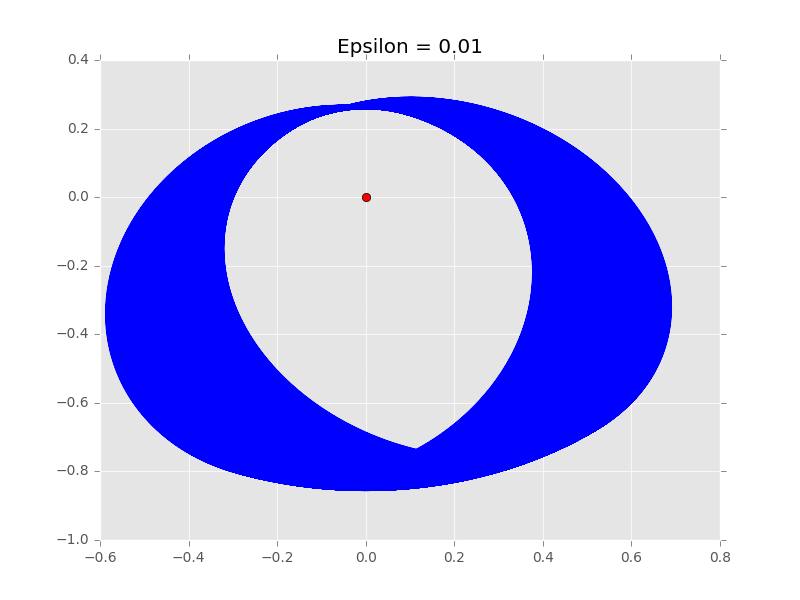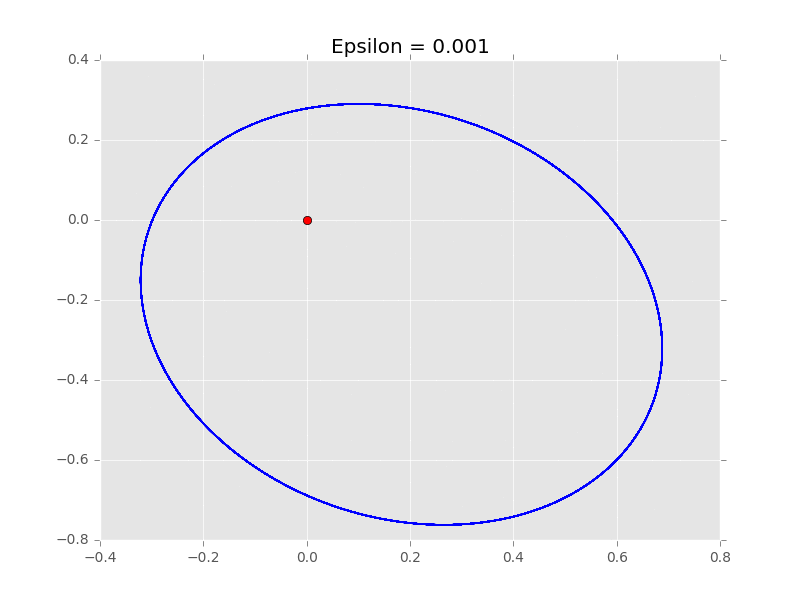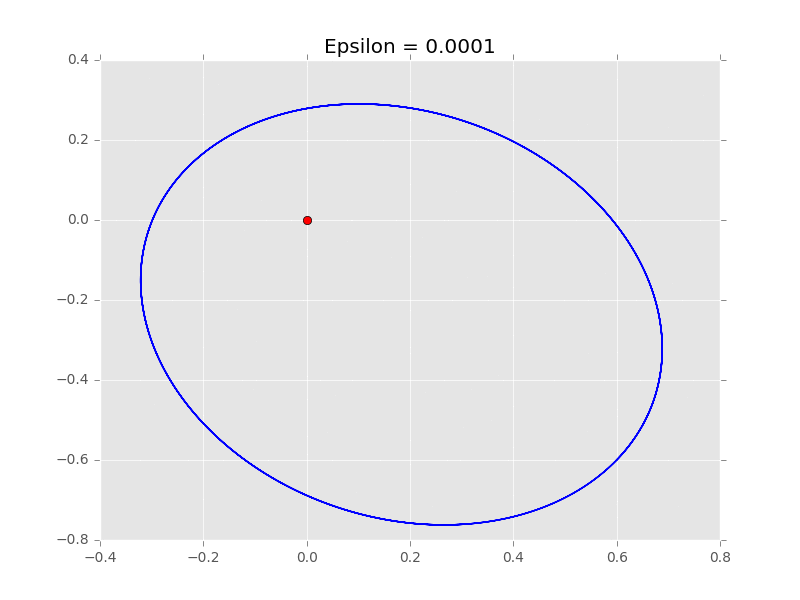
數學定義上,ϵ 應該要多小就能有多小,也就是俗稱的無窮小。不過,電腦終究不是人類,無法處理連續的事物,我們僅能將離散盡可能化小,逼近連續。所以繪製軌道其實算是差和分而非微積分,仍有時間差需要考慮,不可能滿足無窮小的要求。要是時間差太大,繪製出的軌道會有誤差:
ϵ 越大誤差值越大,反之則越小。為了有準確的結果,我們需要一個較小的 ϵ 值,如此才能真正去模擬行星如何運行。
而費曼是這樣說的:
事實上,誤差的大小跟所採用的時間間隔 ϵ 的平方成正比。也就是說,如果我們把 ϵ 縮小一千倍,準確度會提升一百萬倍。前例中,我們採用 ϵ = 0.1 時,準確度已經達了百分之一;若要讓準確度到達十億分之一,我們還得把 ϵ 再縮小一萬倍。
但 ϵ 越小,所耗計算時間越久,不一定越小越好。有可能已經能滿足我們的條件了,卻浪費多餘時間在絲毫的差異上,所以 ϵ 只需要到達我們可容忍的範圍即可。
在這裡,我們設定 ϵ = 0.0001。作為時間間隔的值。
套件概略說明
工欲善其事,必先利其器。要運行程式前,請先確認是否安裝下列套件:
- Numpy
- Matplotlib
Python 本身沒有附帶這些套件,要是才剛下載下來,請安裝這些套件,詳細的安裝方法有請上網查詢。
這兩個套件常常在科學領域使用,彼此扮演不同角色。Numpy 主要處理數值運算,本身以 C 語言優化,所以效率會比普通的 Python 運算快上許多,藉此可以加速計算的速度;Matplotlib 將計算結果以圖像化呈現,有各式圖表可以使用,好比最一般的折線圖、長條圖。我們將以這個套件繪製出結果,讓人容易明白行星的運動。
程式編寫
首先我們要將需要的套件帶入,輔助接下來的模擬:
import numpy as np
import matplotlib.pyplot as plt
from numpy.linalg import norm
from matplotlib import style
style.use('ggplot') #讓圖像變得好看一點,全憑個人喜好
將先前提到的 ϵ 代入,設定其為 0.0001;迭代次數則憑狀況而定,有些時候迭代次數不足,行星會走到一半就結束,原本要的橢圓就會破一個洞,不怎麼完美。一般情形下,我們會將星球的初始位置設定在 1.5 以內,如此才不會運行太久。事實上,我們模擬的目的主要是看其軌道的型態為何,彼此間的距離其實沒什麼關係,在相等比例下,繪製出的軌道基本上會相同,沒什麼必要讓它繞很大一圈。
以下是我們設定的兩個超參數:
epsilon = 0.0001 #時間間隔
n = 100000 #迭代次數
思考一下,星球本身含有那些屬性需要我們考慮呢?位置、速度、加速度,這些數值我們需要記錄下來,為運算必備之元素:
position = np.zeros((n, 2)) #紀錄每個時間點的距離
velocity = np.zeros((2)) #紀錄當下的速度
acceleration = np.zeros((2)) #紀錄當下的加速度
除卻要記錄這些數據外,我們還需要初始值,如此才能知道該如何運作。那模擬星球繞行恆星需要輸入幾個參數呢?位置是一個,而速度則是另外一個;此外,我們在二維空間上運行,所以位置與速度皆有 X、Y 軸方向之分,各兩個參數,於是一共要輸入4筆資料。
輸入資料:
- X初始座標值
- Y初始座標值
- X分量初始速度
- Y分量初始速度
有關輸入參數的代碼如下:
position[0, 0] = float(input("輸入X初始座標值: "))
position[0, 1] = float(input("輸入Y初始座標值: "))
velocity[0] = float(input("輸入X分量初始速度: "))
velocity[1] = float(input("輸入Y分量初始速度: "))
得到參數後,我們便要開始一連串的計算。還記得上頭所寫的方程式嗎?現在我們要將它們轉化為程式碼,讓電腦替我們計算。我們依照費曼書中提到的方式,先算加速度與速度。流程大抵如下:
- 需要知道星球距離恆星多遠:求 r。
- 需要計算兩者間距離三次方的倒數: 求 1 / r3。
- 需要計算星球的速度:求 v。
代碼長得像這樣子:
r = norm(position[0]) #計算離太陽距離
r3 = 1 / (r**3) #計算 1/r^3
acceleration = position[0] * -r3 #計算星球加速度
velocity += acceleration * epsilon * 0.5 #計算星球速度
接下來,我們可以開始一連串的運算了。每回合流程都一樣,我們可以用個迴圈來處理。這是最核心的代碼,等一下移植到三維空間,也是使用下列的代碼,原封不動:
i = 1
while(i < n): #重複n次
position[i] = position[i-1] + velocity * epsilon #計算更新後的星球位置
r = norm(position[i]) #計算恆星與星球間的距離
r3 = 1 / (r**3) #計算 1/r^3
acceleration = position[i] * -r3 #計算星球加速度
velocity += acceleration * epsilon #計算星球速度
i += 1
算完後,我們要繪製出計算後的結果:
plt.plot(position[:, 0], position[:, 1], 'b-')
plt.plot(0, 0, "ro")
plt.show()
整個星球運動模擬程式就大功告成,大致上並不複雜,三、四十行代碼就能搞定。
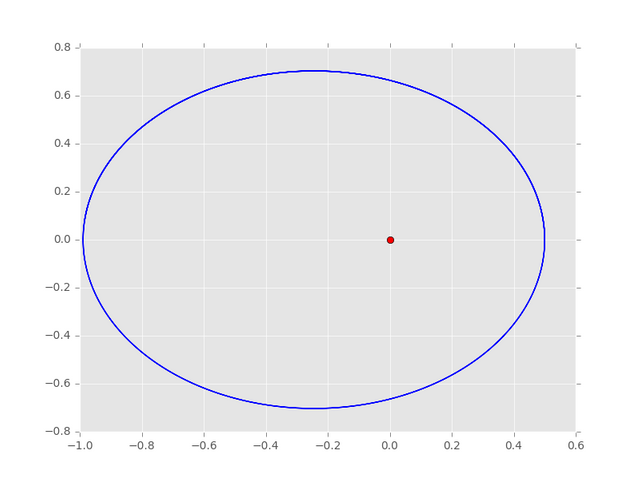
讓我們把《費曼物理學講義》上的參數(vx=0,vy=1.63,x=0.5,y=0)代入測試,看看會得出什麼樣的結果來:
看來還不錯,行星繞著恆星的軌道路徑是一顆豐滿的橢圓,就像蛋一樣。
拓展到三維
其實並不難把行星路徑模擬搬到三維空間運行,所有原理一樣;我們依舊能在各個分量找到它們的相似三角形,再用相同推導方式求出方程式來。唯一不同之處是計算距離的公式需要修改:
但我們使用的 Numpy 套件,其函數本身就可以計算高維度空間的向量長度,也就是求出它們的模長,所以大致上不需做任何修改。需要更動的地方是 Matplotlib 繪圖,原先它只能繪製 2D 圖形,現在我們要把它弄成可以繪製 3D 圖形,整體代碼如下:
import numpy as np
import matplotlib.pyplot as plt
from numpy.linalg import norm
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import style
style.use('ggplot')
fig = plt.figure()
Ax = fig.gca(projection='3d')
epsilon = 0.0001 #間隔
n = 100000 #迭代次數
position = np.zeros((n, 3))
velocity = np.zeros((3))
acceleration = np.zeros((3))
position[0, 0] = float(input("輸入X初始座標值: "))
position[0, 1] = float(input("輸入Y初始座標值: "))
position[0, 2] = float(input("輸入Z初始座標值: "))
velocity[0] = float(input("輸入X分量初始速度: "))
velocity[1] = float(input("輸入Y分量初始速度: "))
velocity[2] = float(input("輸入Z分量初始速度: "))
r = norm(position[0])
r3 = 1 / (r**3)
acceleration = position[0] * -r3
velocity += acceleration * epsilon * 0.5
i = 1
while(i < n): #核心代碼不變
position[i] = position[i-1] + velocity * epsilon
r = norm(position[i])
r3 = 1 / (r**3)
acceleration = position[i] * -r3
velocity += acceleration * epsilon
i += 1
Ax.plot(position[:, 0], position[:, 1], position[:, 2], 'b-')
Ax.scatter(0, 0, 0, c="r")
for angle in range(0, 360): #360度旋轉一圈
Ax.view_init(30, angle)
plt.draw()
plt.pause(.001)
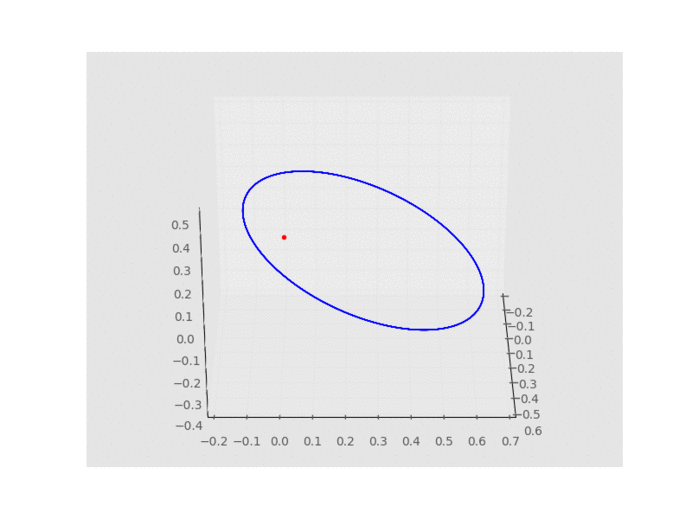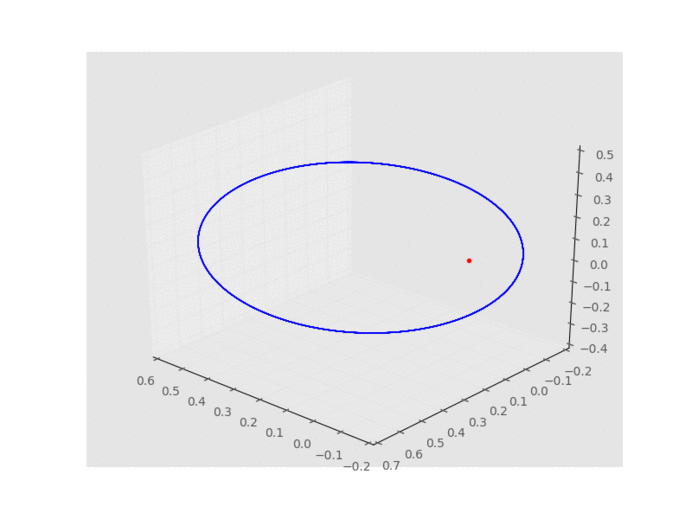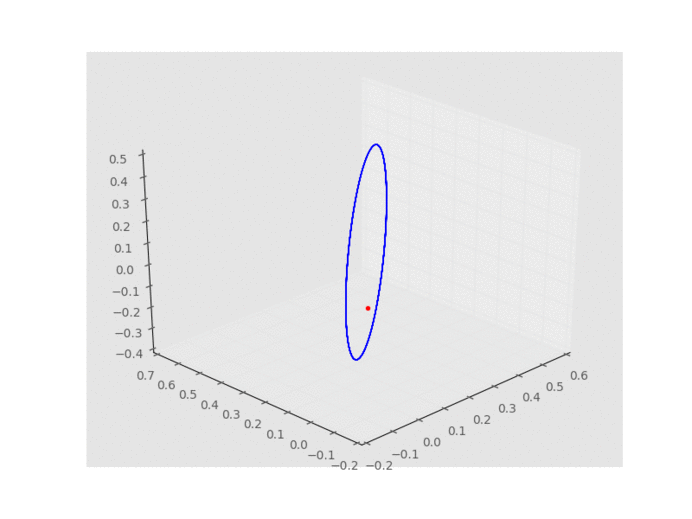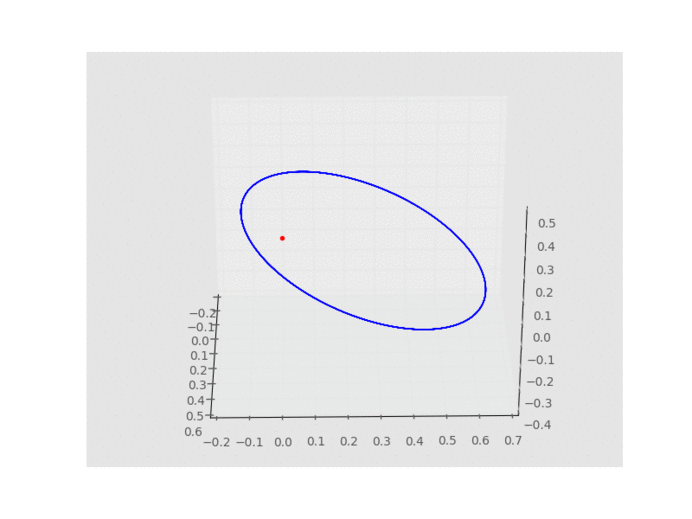
下面是我隨意代參數進去後所得的結果,大家可以自行試試:
有關星球軌道的基礎繪製就在此暫時告一段落,但旅程尚未終了,還有許多進階的事物等著我們探索。
不過,在此之前,你們可以試著修改代碼使其臻於完善,或者就純粹把玩它看看能玩出甚麼新花樣。總之,我期待眾人能有所啟發,能有一些新想法,精益求精,開始創造自己的小宇宙吧!
思考與改進
- 會不會覺得行星已經繞一圈後仍繼續計算有點多餘?有沒有方法可以解決這個問題呢?
- 行星在一定條件下,會擺脫恆星的重力,逕自向外飛去而不復返。是否只能等到計算完才能結束呢?抑或是有特殊的算法可以知道行星是否會脫離?
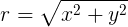
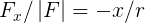
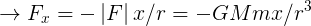
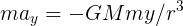
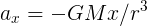
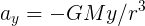
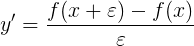
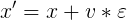
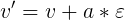
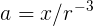
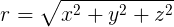
这个覆盖面太广了!!!根本没法吸收知识啊 好厉害的感觉
這的確覆蓋很多東西。我原意是想要將各式學科結合在一起,而不要死板板地限制在一個領域之中。在學校,老師大都侷限於自己專門的領域中授課,各個科目沒什麼交集。這樣感覺不怎麼好,就好比一隻魚被大卸八塊卻不鮮美可口,成了屍塊一般。老實說,學科並非涇渭分明而有個明確的界線,若肯努力去探索,必定可以找到它們的異同處。
台灣最近在鼓吹程式教育,希望整個教育體系能好好納入程式設計。這想法本身不錯,自己也樂觀如是發展,但擔心會流於形式,而失去其中的真諦。
所以我才寫這系列,想作為一個範本供他們參考。這一篇文章本身就是高中領域內的東西來做發揮,行星運行、牛頓力學、向量,沒有超出範圍,如果是好好學習的高中生,應並不難理解當中的理論。這樣一來,在授課的同時便可以結合程式設計,一同學習,不一定要特別開一門資訊課來教導。
不過,我是期望大家都可以學習,好好地體會當中的奧妙啦!只可惜這系列難度有點高,算是一個遺憾。
Great post and very informative. @etzel Have learnt a lot from it.
我對於這個就真的完全沒有概念 @@
不過很歡迎你可以來這裡分享你的所知喔! :)
沒關係,總會有人懂。
我確實很想在這裡分享我所學,有好多東西可以說喔!
可以喔!! 這裡有很多不同專業領域的朋友! :)
屌,很高興又在這平台遇到臺灣人!
應該不難遇到吧!呵!
最近有一對退休夫妻也來這裡了,同樣是台灣人,不知你有沒有看到。
其實也沒這麼容易喔
很高興在這裡認識你,歡迎你加入。 :D
他們的帳號是什麼呢?
@tungjungchen 與 @helenliu兩位,女兒邀他們來這。
有看到他們,很有意思的一家人