Jak optimalizovat své „upvoty“ z pohledu matematika! [část: 2/2]
Právě čtete druhou a poslední část článku Jak optimalizovat své "upvoty" z pohledu matematika! V této části je v několika příkladech demonstrována aplikace upravené rovnice pro odměňování kurátorů, která byla odvozena a vysvětlena v předchozím článku.
← PŘEJÍT NA 1. ČÁST ČLÁNKU
Dále je uvedeno a vysvětleno, co se stane, když hlasování proběhne před uplynutím třiceti minut od publikování příspěvku. V samotném závěru jsou uvedeny všechny důležité poznatky, které v souvislosti s hlasováním z obou článků vyplynuly.
Aniž by se mi podařilo odhalit příčinu, článek psaný v HTML se zobrazuje správně pouze na platformě BUSY.ORG. Steemit článek od první kapitoly předělal do kurzívy. V první části tento problém nenastal, zvláštní. Mrzí mě to !!! :–(
6 VZOROVÉ PŘÍKLADY
6.1 Planktoňák hlasuje pro příspěvek, který bude trendy:
Váha jeho hlasu je v = $ 0,1. Příspěvku udělil hlas jako první přesně 30 minut od jeho publikování, tj. P0 = 0 a t = 1. Jaká bude zhruba jeho odměna, když po týdnu odměna příspěvku dosáhne hodnoty PT = $ 5?
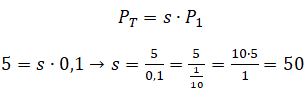
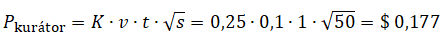
Všimněte si, že výsledná odměna je 50 krát vyšší jak váha jeho hlasu. Ověřit to lze ze vztahu (4):
Po dosazení známých hodnot do rovnice (8):
Planktoňák docela boduje, protože si vydělal 1,77 krát více, než byla váha jeho hlasu. Celkem dosáhl nárůstu o 77 % → 0,1 × (1 + 0,77) = 0,1 × 1,77 = 0,177.
Na první pohled to zní hezky – při výsledné odměně článku $ 50 by dokonce vydělal $ 0,559 (s = 500) –, jenže kdy se v takovém případě povede být skutečně první?
Co z toho plyne? Výše naší odměny se zvyšuje s druhou odmocninou parametru s, tzn. pro s = 50 → √50 = 7,07 krát; pro s = 500 → √500 = 22,36 krát; pro s = 100 → √100 = 10 krát.
6.2 Když velryba najde trendy příspěvek a rozhodne se pro něj hlasovat:
Váha hlasu velryby je v = $ 40. Ta se má! Výchozí odměna příspěvku je P0 = $ 460. Velryba hlasovala mezi posledními a jelikož se navýšená odměna P1 = $ 500 do konce týdne už téměř nezvýšila, můžeme zjednodušeně považovat P1 = PT, tj. že se navýšená odměna rovná té výsledné na konci sedmi dní od publikování. Z toho plyne s = 1.
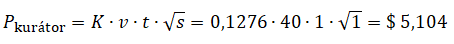
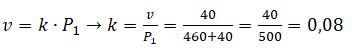
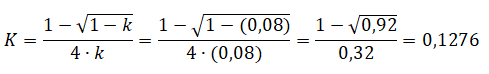
Po dosazení známých hodnot do rovnice (8):
Parametr K = 0,1276 byl získán následovně:
Velryba si vydělala zhruba jednu osminu z váhy svého hlasu, neboť při malém zaokrouhlení 5,1 na 5,0 → 40 / 5 = 1/8. Z toho plyne, že množství SP, které máte, resp. váha vašeho hlasu je rozhodující.
6.3 Když planktoňák napodobuje velrybu:
Představte si touž situaci 6.2, nýbrž s váhou hlasu v = $ 0,1 Co bych za to dal! Po hlasování bude navýšená (resp. i výsledná) odměna příspěvku P1 = PT = $ 460,1. Pro k = 0,1 / 460,1 = 0,000217, resp. K = 0,125 jeho odměna bude:
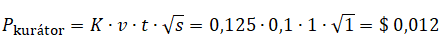
Julián s nadšením oznamuje, že se jedná o skoro stejný případ, jako tomu bylo u velryby. Jenže ke vší smůle nemluví o výši odměny, ale hodnotě K, která se v obou případech blíží 0,125. Uznávám ale, že zjištění, že je jedno – kdo jste – pokud hlasujete pozdě pro trendy příspěvek, je zajímavé. Díl, který každý z váhy našeho hlasu v tomto případě dostaneme, je totiž stejný → 1/8.
6.4 Co když podpořím průměrný příspěvek:
Svým hlasem o váze v = $ 1 podpoříme příspěvek s výchozí odměnou P0 = $ 0,03, a to chvilku po uplynutí třiceti minut od publikování příspěvku (t = 1). Článek po týdnu dosáhne výsledné odměny PT = $ 1,72.
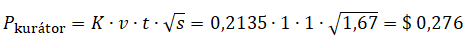
Naše odměna po dosazení k = 1 / (0,03 + 1) = 1 / 1,03 = 0,97, resp. K = 0,2135 a s = 1,72 / (0,03 + 1) = 1,72 / 1,03 = 1,67 do rovnice (8) bude:
I když nebudeme prvním hlasujícím, díky násobně vyšší váze hlasu, v porovnání s hodnotou výchozí odměny příspěvku, dosáhneme příjemného výdělku → téměř 1/3 váhy našeho hlasu.
6.5 Naskakujeme do rozjetého vlaku:
Představte si tu nejhorší možnou situaci. Při čekání „na třicet minut“ od publikování příspěvku jste usnuli a než jste se stihli rozkoukat, jeho (výchozí) odměna dosahovala už takových hodnot, že ji Váš hlas vůbec nezměnil. V takovém případě K dosahuje minimálních hodnot a s je téměř rovno 1.
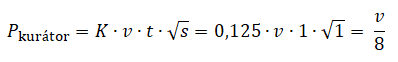
Pokud jste si doteď mysleli, že záleží na výchozí odměně trendy příspěvku, tj. zda u něj stojí $ 400, anebo $ 2500, zklamu Vás. V tomto případě rozhoduje pouze váha Vašeho hlasu, viz následující úprava rovnice (8):
7 PORUŠUJEME PRAVIDLO „30“
Ve všech předešlých případech jsme uvažovali s udělováním hlasů po uplynutí třiceti minut od publikování příspěvku. V těchto případech bylo vždy t = 1. Hlasovat můžeme ale i dříve. A někdy se to dokonce vyplatí.
Když kurátor odevzdá hlas, navýšená hodnota odměny, jak již víme, bude P1. Nově definujeme odměnu v čase t = 30 minut od publikování P30. Hodnota tohoto nového parametru je s30-násobkem navýšené odměny P1. Ke stanovení výsledné odměny na konci týdne použijeme stejnou konstantu ‚s‘ jako v předešlých případech. Dále navíc uvažujeme, že výsledná odměna PT je c-násobkem odměny P30, tj. v čase t = 30 minut od publikování. Takže:
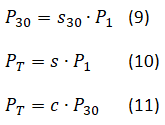
Nejprve vyjádříme parametr P30 ve vztahu (11). Poté dáme do rovnosti vztahy (9) a (11) a za PT dosadíme vztah (10). Drobnými úpravami dostaneme:
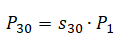
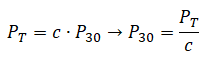
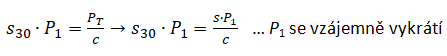
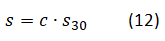
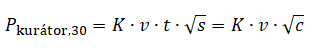
K tomu, abychom zjistili, zda se nám vyplatí hlasovat dříve jak třicet minut od publikování článku, si odvodíme vztahy pro výpočet odměny ve dvou různých situacích:
1) Hlasujeme přesně 30 minut od publikování, t = 1:
Možná si říkáte: „Jak to že se s = c?“. Taky jsem se ptal. Pokud hlasujete v čase t30, navýšená hodnota odměny P1 se bude rovnat odměně P30, která je definovaná právě jako odměna v čase t30. Aby se P1 a P30 rovnaly, ze vztahu (9) vyplývá, že s30 se musí rovnat 1. Po dosazení s30 = 1 do vztahu (12) poté vyplývá, že:
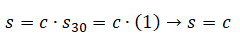
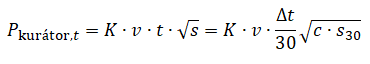
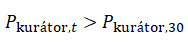
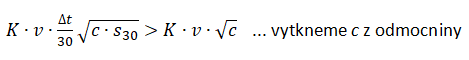
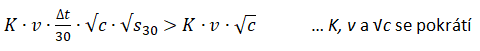


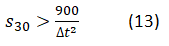
2) Hlasujeme kdykoliv před uplynutím 30 minut, t = 0–1:
kde ∆t je doba v minutách, po které jsme od publikování příspěvku hlasovali.
Jelikož nás zajímá, zda je výhodné hlasovat před uplynutím 30 minut, požadujeme, aby odměna v čase t < 30 minut byla větší jak odměna v t = 30 minut, tj.:
Pokud si myslíte, že odměna článku může od vašeho hlasování ještě dále vzrůst více jak s30-krát, poté hlasujte. V opačném případě se to nevyplatí.
Pár příkladů:
7.1 Deset minut od hlasování je odměna článku P0 = $ 99. Po vašem hlasu o váze v = $ 1 dosáhne navýšená odměna hodnoty P1 = $ 100. Když dosadíme t = 10 do vztahu (13), získáme 900 / 102 = 9. Aby se nám vyplatilo pro příspěvek v tuto dobu hlasovat, jeho odměna P30 by musela dosáhnout hodnoty $ 100 × 9 = $ 900 nebo více. Pokud si myslíte, že za dvacet minut odměna příspěvku této či vyšší hodnoty nedosáhne, s hlasováním počkejte.
7.2 Dalším příkladem může být situace, kdy má odměna příspěvku v čase t = 25 minut hodnotu P0 = $ 69. Pokud svým hlasem zvýšíte odměnu na P1 = $ 70, aby se Vám vyplatilo hlasovat, musela by za posledních 5 minut odměna P30 dosáhnout minimálně hodnoty $ 100,8, neboť 900 / 252 = 1,44 a 70 × 1,44 = $ 100,8.
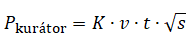
8 PÁR SLOV ZÁVĚREM
Vaše odměna se zvyšuje s druhou odmocninou parametru s zohledňujícího následný růst odměny příspěvku od doby, kdy jsme hlasovali. Čím více získá příspěvek následných odměn po našem hlasování, tím větších zisků dosáhneme.
Výši vaší odměny dále lineárně ovlivňuje váha vašeho hlasu. Při hlasu o váze $ 10 bude váš profit desetinásobně vyšší jak u hlasu o váze $ 1.
Pokud budete příliš pozdě hlasovat pro trendy příspěvek, výše vaší odměny bude odpovídat osmině (v/8) váhy vašeho hlasu, nezávisle na výsledné odměně příspěvku PT.
Pokud budete hlasovat po třiceti minutách od publikování příspěvku, jako první hlasující obdržíte minimálně čtvrtinu váhy vašeho hlasu (v/4), a to nezávisle na výsledné odměně za příspěvek PT.
Pokud uvažujete hlasovat před uplynutím 30 minut od publikování příspěvku, musíte si být jisti, že odměna P30 vzroste vůči navýšené odměně P1 (900/∆t2) krát. V opačném případě se to nevyplatí.
DÍKY ZA VÁŠ ČAS! THANK YOU @jga !!!
9 POSLEDNÍ OPÁČKO
Kurátorská odměna se stanovuje pomocí následující rovnice:
Jenom tiše zírám. Velmi obsáhlé a vyčerpávající :-D
Pro tyhle případy je v závěru vždycky shrnutí. To jsem se naučil ve škole. Ještě předtím než člověk začne něco číst musí: 1) Prečíst úvod s motivací; 2) přečíst závěr. Pokud potom uznáš, že to za nic nestojí, vnitřek nemá cenu číst. Škoda, že jsem se to naučil až po pročtení x desítek nudných a zbytečných stran. Doufám, že v tvém případě byl zvolen ten "správnější" postup… :-D :-D !!
Mám ponětí, že něco takového existuje. Tuším (a teď už i vím), že se dá skoro vše spočítat ;-). Otázka pro mne zní: má smysl tím přetěžovat obvody? Informace se musí třídit a tak jsem si uložil do paměti existenci tohoto výpočtu a prozatím mi to stačí ;-)
Ono z toho vyplývá spousta věcí. Třeba, když se nad tím člověk zamyslí, to jasně ukazuje na to, jak lidi, co si objednávají boty (pokud hlasují ve velkých sumách), znemožňují skutečným čtenářům získat nějakou odměnu za čtení, najití příspěvku, případně jeho sdílení. Boti nečtou. Boti jsou programy, co článek najdou v mžiku vteřiny atd. atd. Další věc je, pokud si někdo sám "upvotne" svůj příspěvek. K tomu se ale váže více věcí a uvažoval jsem, že něco najdu a napíšu i o tom. Jsou to všechno otázky etikety… :o)
Ale pokud si objednáš bota s nějakým časovým odstupem (třeba pár dnů), tak ti čtenáři co hlasovali na startu mají o to větší odměnu, ne? Ten čas se tam také zohledňuje. Druhá věc je že větší odměna a více upvotů tě posouvají v Trending nahoru, tak je asi motivace ty boty použít co nejdříve.
Bravo! Skvěle!
Great job, @jga, thank you! Skvělá práce, @khjk, patří Ti obrovský dík!
Neříkám, že budu těchto rovnic využívat, ale bylo dobré si je prohlédnout a zamyslet se nad nimi. (Navíc jsem se po jisté době opět setkal s limitami.) Sám se totiž snažím, alespoň většinou, hlasovat pro příspěvky, ketré považuji za zajímavé a líbí se mi. Případně se svým slaboučkým hláskem snažím podpořit nováčky a komunitu. (Nebo se naopak svým slabým záporným hlasem snažím bránit Steemit.) Ale jiní těchto rovnic třebas využijí. Steemit je totiž i o kurátorství, vždyť jak jinak by příspěvky autorů získaly odměnu. ;)
Myslím, že – mimo vytváření – je hledání kvalitního obsahu, jeho čtení a hodnocení jednou z hlavních myšlenek Steemitu. Rozhodně je správné řídit se pravidlem to se mi líbí – to podpořím. Znalost toho, jak to funguje, možná trochu jde proti tomu, ale… ale… Určitě si rozumíme (—: Jakmile jsou ohodnocováni i kurátoři, dá se za aktuálních podmínek očekávat, že se budou snažit chovat co nejefektivněji.
Máš pravdu!
Kurátoři, tedy všichni, kteří pro daný příspěvek hlasují, mají na Steemit velmi důležitou úlohu. Bez jejich hlasu by nedošlo ke zviditelnění daného příspěvku. Ano, kolikrát se stane, že díky silným hlasům botů, jsou více vidět příspěvky méně kvalitní než jiné, ale věřím, že postupem času se to bude měnit. Přeci jen je jádro komunity velmi rozumné a silné. Proto mohou další HardForky přinést podstatné změny.
Až přijde v platnost HF20, tak to, co jsem tu psal, můžeme zahodit. :D Má se to údajně "nějak" "malinko" měnit. Nemá ale stanoven přesný datum vypuštění, pokud vím.
Má se měnit čas, kdy si kurátor a autor dělí kurátorskou odměnu z 30 na 15 minut. Zda se změní ještě něco, to je ve hvězdách (nebo v příspěvcích svědků). Přesné datum ani přesný blok prozatím stanoven nebyl.