SLC S22W3//Equations and Systems of equations
Hello friends of steemit today I will be participating in this steemit learning challenge hosted by @khursheedanwar titled equations and systems of equations.
• Task 1
• Explain difference between linear and non linear systems of equations. Provide examples of each type of system of equation and describe their general forms.
| LINEAR SYSTEMS | NON LINEAR SYSTEMS |
| the output of linear systems is directly proportional to the input | the non linear systems of equations is not directly proportional to the input |
| it general form can be expressed as yx+bg=c | it's general form can be expressed as yx²+bg²=c |
| their graphical representation is seen by them producing hyper planes or straight line | their graphical representation are they produce parabolas curves and circles |
| the sum of solution is also seen as a solution | the sum of solution may not be a solution |
| the solution can be found using direct methods like eliminating or substitution | solution require complex method like graph analysis or numerical method |
| their examples can be expressed as 2x+3y=6 | x²+y²=1 |
• Task 2
• Describe any one method for solving system of linear equations and share atleast one step by step algebric example.
(It should be other than substitution, elimination and graphing method)
Cross multiplication method is another system of solving systems of linear equation particularly dealing with cross multiplying when an equation has two variables and it is simply cross multiplying the constants and the coefficient to find values of the variables in the equation.
Steps to solve using cross multiplication method
1 write down the equation in standard form
2 Cross multiply to express the variables as coefficient
3 Solve for the variables in the equation using the answers gotten from the cross multiplication.
Example
An equation given
2x + 3y =6
4x - y =5
Solution
• Task 3
• You need for solving following system of linear equations:
(a)
x + 2y = 7
3x - 2y = 5

Now solve for y by substituting x =2
Done for a now b
(b)
4x + 6y = 2
x - 2y = 3
Now solve the x first
Solve for y
Conclusion
(You are required to solve these problems at paper and then share clear photographs for adding a touch of your creativity and personal effort which should be marked with your username)
• Task 4
Scenario number 1
Suppose there's a company producing two products, A and B.If cost of producing x units of A and y units of B is given by system then;
2x + 3y = 130 (cost of materials)
x + 2y = 110 (cost of labor)
If company wants for producing 50 units of product A then calculate how much units of product B they may produce?
(Solve the above scenerio based questions and share step by step that how you reach to your final outcome)
Scenario number 2
• Suppose there's a bakery producing two types of cakes which are vanilla and chocolate.If cost of producing x cakes of vanilla and y cakes of chocolate is given by system then;
x + 2y = 80 (cost of ingredients)
2x + y = 70 (cost of labor)
If bakery wants for producing 30 cakes of vanilla then calculate how much cakes of chocolate can they produce?
So in conclusion the company can produce 10 units of product B when producing 50 units of product B
Scenario 2
Therefore the bakery can make 25 chocolate cakes when producing 30 cakes of vanilla.
With this I have come to the end of my participation I will now like to invite @bonaventure24 @josepha @lirvic and @chiagoziee to also take part in this learning challenge





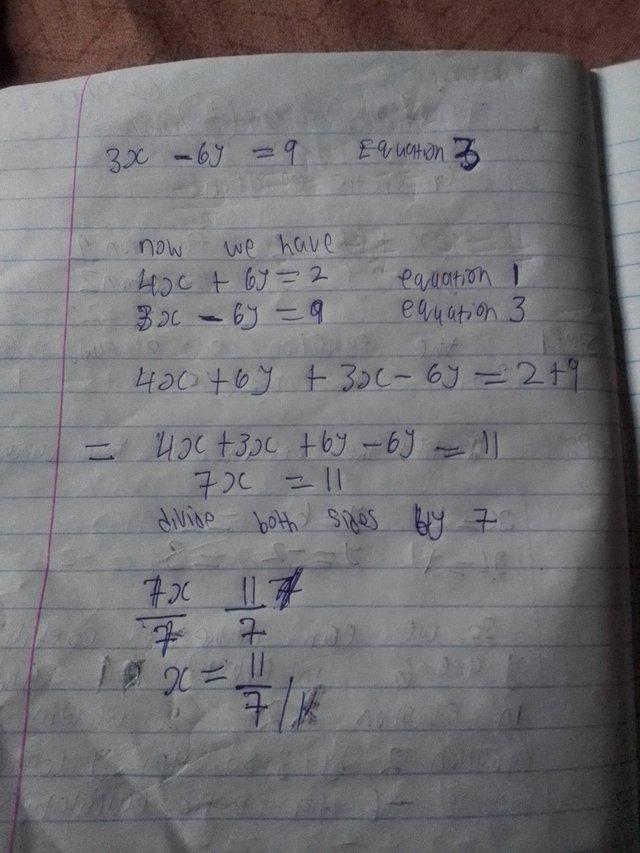
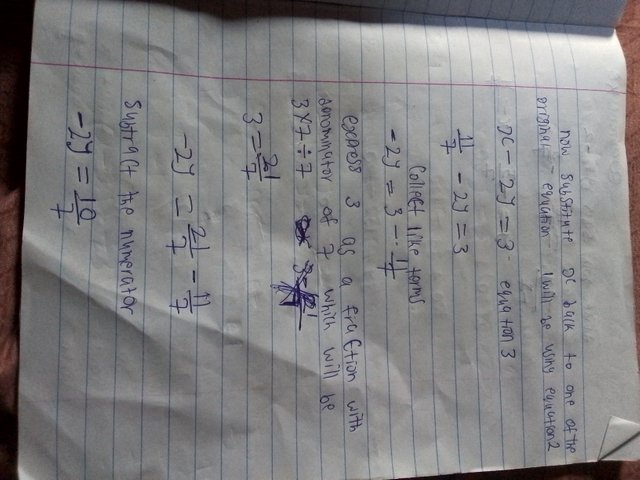




https://x.com/ahmneska/status/1875587630429302799?t=fSENfGWWJCmNM7AN_QJA0w&s=19