Blockchain Fundamentals: What is a Merkle Tree?

Let’s start with a quick definition from the book Mastering Bitcoin by Andreas M. Antonopoulos:

A merkle tree, also known as a binary hash tree, is a data structure used for efficiently summarizing and verifying the integrity of large sets of data.

This gives us a great high-level starting point. However I think it’s a challenge to capture the significance of merkle trees using words alone. In my experience it’s the type of concept that’s better defined by showing how it works instead. We’ll do this through building our own Merkle Tree. However beforehand, we need to go through a quick primer on hashing first.

Hashing

Hashing functions are mathematical algorithms that take inputs and provide unique outputs. Some of the most common hashing functions are MD5, SHA-3, and SHA-256 — the last of which is used by Bitcoin.

These hashing functions will produce unique values that you can later use to “represent” the inputs. It’s important to recognize that these values will exclusively represent the current state of any given input. “State” in this context can represent a number of things. For example, adding a single word to the end of a file or simply changing its contents in any manner. When this happens, the file in question can be said to now hold a new state.

Let’s demonstrate how this works in detail.

(Note: to follow along you must be running macOS).

Example

First, open up Terminal and go to your home folder. Then create a new directory called merkletrees.

cd ~ && mkdir merkletrees && cd merkletrees

Now create a file called a.txt

touch a.txt

Then we can run the built-in md5 command on our newly created file.

md5 a.txt

The result should be the hexadecimal string: d41d8cd98f00b204e9800998ecf8427e. (For brevity sake, I’ll refer to these hash values by the first seven characters like d41d8cd. I find this makes reading easier.)

So what happened here? We just produced a unique “hash” value — d41d8cd — that represents the current state of a.txt. The state here happens to be an empty file. You might find it interesting that an empty file outputs a hash at all. This is partly unique to the md5 algorithm as it will always produce d41d8cd for empty files.

If we change the contents of a.txt, the hash will also change. We can update the name and even the extension of the file without the hash changing. Again, what matters here are the contents itself. Give it a shot by going back to Terminal and running this in the same directory:

echo “hashing is awesome” >> a.txt && md5 a.txt

You should get the hash ca00359cc149a5622c5ba87a93d8abb9 or ca00359 for short. Our file now contains the text “hashing is awesome” which means that it also holds a new state — represented by the unique hash ca00359.

Growing The Tree

There are different types of Merkle Trees. With many blockchains however, we’re primarily concerned with transactions between two entities (Person A sends $10 to Person B). Therefore “Binary Merkle Trees” are what projects like Bitcoin use.

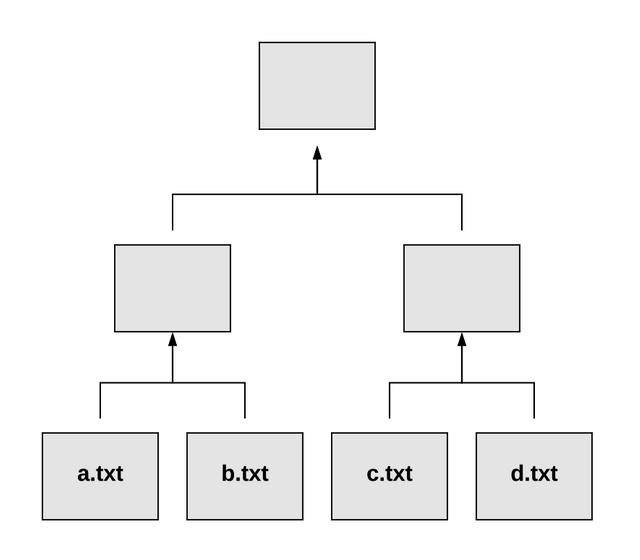
As the same suggests, a Binary Merkle Tree is a data structure in which each node has at most two children. This means we combine two inputs together to obtain a single output. When we have multiple pairs of inputs, a tree structure develops like this:

Relating this back to our previous example, a.xt in diagram 1 would be the hash ca00359. We haven’t created a second file yet, but if we did, we could take its hash and combine it with ca00359. The next step would be to run this “combined” hash through MD5 again to get the parent hash. We continue this process until we’re left with a single value called the Merkle Root.

Adding Branches

Imagine our a.txt file is given three new siblings: b.txt, c.txt and d.txt—all of which have unique content.

First, open Terminal and delete the previous a.txt file we made earlier.

rm a.txt

Next, run the following command.

echo "Hello from a.txt" >> a.txt && md5 a.txt &&
echo "Hello from b.txt" >> b.txt && md5 b.txt &&
echo "Hello from c.txt" >> c.txt && md5 c.txt &&
echo "Hello from d.txt" >> d.txt && md5 d.txt

You should see an output like this:

MD5 (a.txt) = c95c68d91441ba192ada81c9cfb2abe7
MD5 (b.txt) = 80262782d5961c452eae5de9991af0fd
MD5 (c.txt) = 0bfe75f719adf6450bb8be8e10126383
MD5 (d.txt) = 10fa7f973f6ec6682e1a6f4570a89861

We just generated a list of hashes from our four unique files like we did with a.txt. We’ll use these to build the tree.

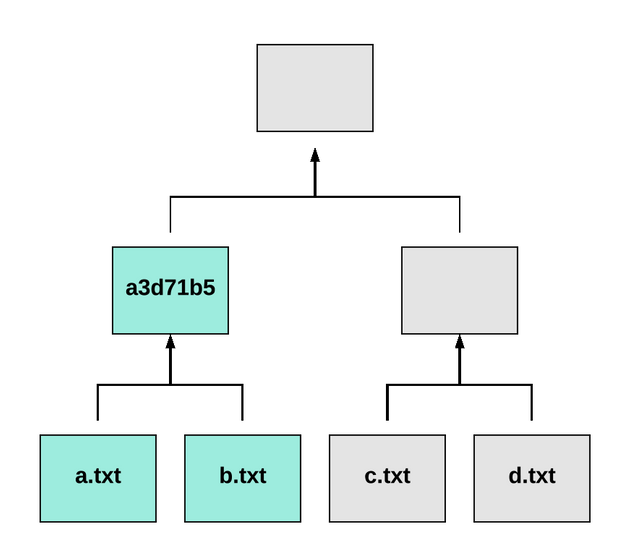
Let’s begin by taking the unique hash of a.txt and _joining it with the unique hash of b.txt. The result becomes this:

c95c68d91441ba192ada81c9cfb2abe780262782d5961c452eae5de9991af0fd

Notice at the moment we’re only combining the hash of a.txt with the hash of b.txt. The next step is to run this combined value through MD5 once more to produce our parent hash.

We can do this by running the following:

md5 <<< "c95c68d91441ba192ada81c9cfb2abe780262782d5961c452eae5de9991af0fd"

Which will give us:

a3d71b58e08759e6245667fb6f4770b6

Congrats! We just produced are first parent hash! We can now say that the current state of a.txt and b.txt are represented by a3d71b5.

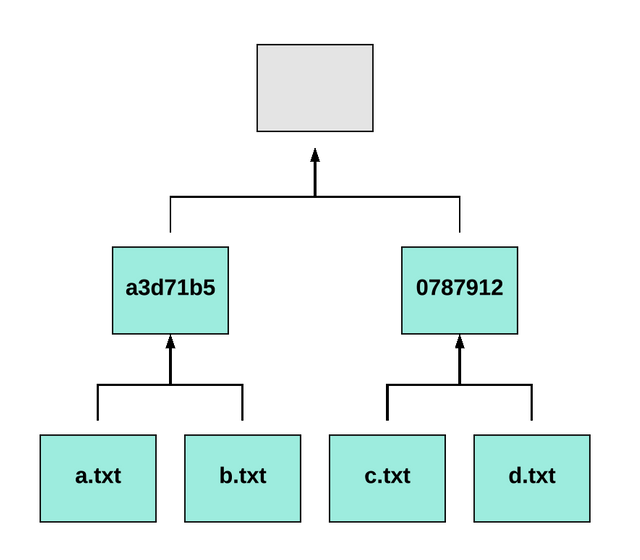
Now let’s repeat this with the hash of c.txt and d.txt. Remember that the former is 0bfe75f and the latter 10fa7f9.

md5 <<< "0bfe75f719adf6450bb8be8e1012638310fa7f973f6ec6682e1a6f4570a89861"

Which produces:

078791272b0b48b7bb7004ebc1b22123

And now our updated tree looks like this:

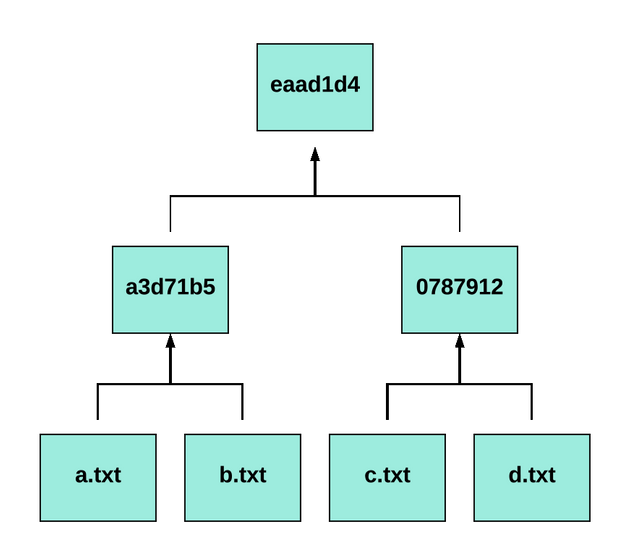
Almost done. The last step is to combine the two parents together to achieve the highly anticipated Merkle Root.

We’ll first combine the two parent hashes a3d71b5 and 0787912. Then run the combined value through MD5 again, like this:

md5 <<< "a3d71b58e08759e6245667fb6f4770b6078791272b0b48b7bb7004ebc1b22123"

Which produces our Merkle Root:

eaad1d42b754612a4249bcbd95f0b734

The Merkle Tree is now complete!

Why Are Merkle Trees Important?

Merkle Trees are really important because they allow for “Merkle Proofs”. These enable us to quickly verify that a given input has been included in a particular data set — and in what order.

Merkle Trees are also really efficient. They allow us to compress large data sets by removing all superfluous branches while keeping only the ones we need to establish our proof. In the Blockchain world, this means Merkle Trees provide the following critical features:

1. Ability to verify whether a transaction is included in a block
2. Light-clients (since we don’t have to download the entire chain)
3. Overall performance and scalability
4. Simplified Payment Verification or (SPV)

There is much more to discuss regarding Merkle Trees including how they operate within other blockchains like Ethereum, how they’re used in scaling solutions, etc. However since this is just a fundamentals article I’ll be touching on those topics separately.

Suffice it to say, once you grasp the basics of Merkle Trees you can really begin to appreciate the security and efficiency of Blockchain data structures. This really is amazing and exciting technology!

If you want to start diving into more advanced Merkle Tree topics, I highly suggest Vitalik Buterin’s article entitled. “Merkling in Ethereum”

Good luck!