符文名字的小知识
最近在了解符文相关的知识,觉得还是有一些东西比较有趣,也在从不断的了解的过程中慢慢的理解符文。
现在大家都知道,符文相对于铭文有以下几个特点:
- 数据写在OP_RETURN里面,而不是写在taproot脚本里
- OP_RETURN里面最多只能装80字节的数据,而taproot理论可以装4M的数据,像runestone那个铭文,大小就接近了4M,也就是铭文可以存储大量数据,而符文存储数据限制较大
- 铭文更适合NFT,本来也是NFT,BRC20是在ord的索引上再加了一层索引来实现的,也是被Casey诟病的,而符文是一个FT协议,不适合做NFT
- 铭文的铭刻需要提交和揭示两笔交易,而符文只有部署的时候才需要提交和揭示两笔,后续均只需要单笔转账就行
- 符文可以单笔转账转移多个资产到多个地址
可以看出,两种协议其实互不冲突,他们在ord的代码中也是平级的,铭文做NFT,符文做FT。大家说的符文和铭文的比较,我认为是符文和BRC20的比较,这样才有比较的意义。
要讲什么?
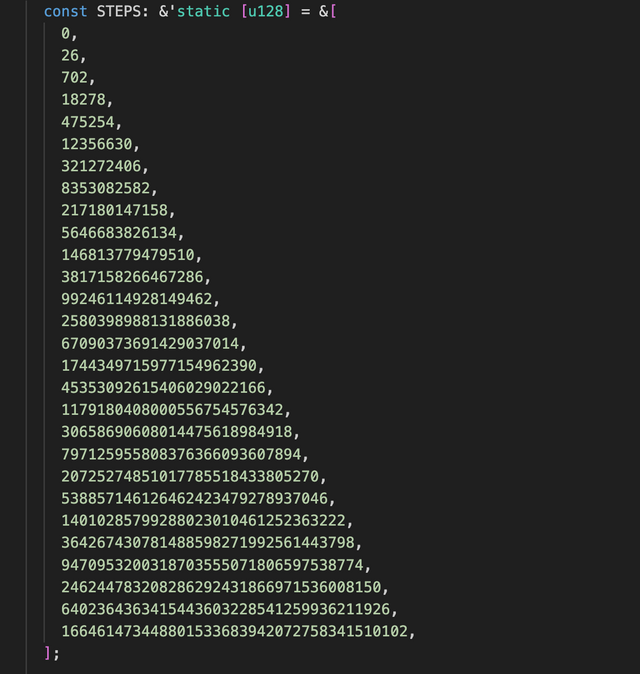
好了,这些背景应该大家都比较清楚了,今天主要想分享一个比较有意思的东西,就是符文的名字,先放一张符文代码中的代码块:
看不懂?没关系,先放这,后面再来解释(如果你觉得你对数字有天赋,不妨试试看一下其中的规律)
FT代币的名字
都知道代币会有个名字,不管ERC20,BRC20还是Rune,发行代币一般都是用一个名字来表示,这样可读性更高,就像大部分用户都知道USDT这个名字,但是很少人会去记USDT的合约是多少,那个太不直观了。
BRC20由于是存储了一个json数据,而代币名字是json中的一个字段,字段值是一个字符串。将这个json转成字符串后用ASCII编码转成数字铭刻到链上,所以代币名字就是被ASCII编码的。
用字符串的ASCII的编码的好处是比较直观,和字符串的转换也很方便,不好的地方就是,浪费空间大,也就是同样的存储空间,能够使用的名字数量少,这是因为使用ASCII码,一个字节只能存储一个字符,而符文中,数据存储的资源是很宝贵的,一定要充分的利用。
符文中的名字编码使用了一种叫调整后的26进制编码,这里有两个部分需要理解,一个是调整,一个是26进制。我第一次听这个的时候还是不明白,什么叫调整?怎么调整?
26进制介绍
26进制,这个应该大家多多少少可以想象,毕竟2进制,8进制,10进制,16进制,都很熟悉,这里26进制和这些进制原理差不多。注意这个Rune名字的编码和BASE64,BASE58,BASE32这些其实是不同类型的。
在符文中,名字在链上是由一个128位的无符号整数数字来表示的,也就是16字节,对,就是一个数字,计算机里都是数字啦,只是编码方式不同而已。占用16字节,如果是铭文那种方式,也就最多支持16位字符串长度,而符文最多是可以支持28个字符长度的。那这是怎么实现的呢?
怎么调整的?
下面我就对比大家所知的进制与这个调整后的26进制来解释一下为什么这里要叫调整后。我们已经知道了名字就是一个数字,但是这个数字怎么转成可读的字符呢?符文的名字设计规定了只能使用A-Z的26个大写字母来组成,这里的A-Z,我们就把他想象成0-9这些数字。
我们知道2进制中,只有0,1两个数字,8进制中只有0-7八个数字,而16进制中是0123456789abcdef共16个符号,而26进制,就是用A-Z共26个符号来代表。
然后来看看进位,2,8,10,16进制中,当每一位上的数字达到最大后,就往高位进位,比如2进制的1,如果加上1,由于2已经达到最大位了,所以要进位,就表示成10,再看8进制的7,再加1后,变成了10,再看10进制9,加1个变成10,16进制的f,加1后变成10,发现规律了吧,进位后,高一位用1表示,原来那位,用数字0来表示,这就是进位。
这里要特别说明的是,由于0在数字前面时不改变数字大小,所以进位后,使用了数字排序中的第2个数字1来表示,而不是0,如果用0来表示,那么9+1应该表示成00,这就是错误的了。
好了,已知的进制表示方式大概了解了。再来看看如果是26进制呢,A-Z分别是表示了0-25,那Z加1后是多少呢?如果按照刚才的规则,那么Z+1后,应该是BA,为什么呢,进位后高位用第2个符号表示,原始位用第一个符号表示,就应该是BA,但是很明显,这样做其实是不合理的,数字进位不用第一个符号0表示的原因刚才讲过了,但是这里26进制全部是使用的字母,数字最前面的A的有无对数字的大小应该是有影响的,比如AA和A,应该是不一样的,而00和0的大小是一样的,所以这里需要进行一定的调整,以使AA和A表示的数字大小不一样。调整的规则如下,当符号位置是在个位时(最低位),A-Z分别代表0-25这26个数字,当符号位置不在个位时,A-Z分别表示1-26的数字,也就是他们代表的数字要加1。所以,Z加1后用AA表示,而不是用BA表示,也就是是AA和数字26是对应的。
再来看AA如何解析成26呢?这和其他的进制转换方法是类似的,像16进制的10,计算方式就是 1 X 16+0 = 16, 16进制的111转成10进制就是 1 X 16 X16 + 1 X 16 +1 = 273。再来看26进制的AA,非个位的A表示1,所以这个A代表了1 X 26, 个位的A表示0,所以就是0,所以AA=1 X 26 + 0 = 26。
小测试
好了,以上就介绍完了调整后的26进制是如何将字符和数字进行转换的,下面就出几个名字,大家看看能自己转成数字不:A,AA,AB,ZZ,AAA,AAAA?
答案是,0, 26,27,701, 702,18278,,你算对了吗?可能细心的朋友发现了端倪。我们再回到前文给出的那张图,没错,那一堆看不明白的数字,如果转成26进制的符号,其实就是A,AA,AAA,AAAA,AAAAA,........哈哈,谜底揭晓了。
小补充
这里还有一个问题,上面代码里数组的前面27个数字,都可以解析成A,AA 。。。 27个A这样的符号,但是最后一个数字解析出来后是这样一个符号BCGDENLQRQWDSLRUGSNLBTMFIJAV,这是一个28个字符的名字,而不是28个A,他是符文能支持的最大的名字,这个名字加1后是BCGDENLQRQWDSLRUGSNLBTMFIJAW,但是这个符号是不能部署成符文的。这是为什么呢?
上面其实提到,符文名字是由一个uint128,也就是128位的无符号整数来表示的,而128位的数字是有上限的,这个上限就是数字166461473448801533683942072758341510102,是2的128次方-1,而这数字按照刚才的规则转换成符号,就是BCGDENLQRQWDSLRUGSNLBTMFIJAV。
好了,今天就介绍到这里,后面我们再来讲讲符文的长度是怎么按照区块高度来判断是否可以部署的。
后记
最后,如果有人部署了BCGDENLQRQWDSLRUGSNLBTMFIJAV这个符文,你会去打一个吗?