SLC-S22W4//Linear and Quadratic equations equations."
Hello steemians today I will be taking part on @khursheedanwar learning challenge titled linear and quadratic equation
• Task 1
• Explain difference between linear and quadratic equations. Provide examples of each type of system of equation and describe their general forms.
| feature | linear equations | quadratic equation |
|---|---|---|
| general forms | ax + b= 0 | ax² + bx +c= 0 |
| Degree | it is always in raised to power 1 or has no power | there are always raised to power 2 or always in second degree | graph shape | they take the form of a straight line in a graph | they take the shape of a parabola in a graph |
| example | they always have one solution | they have more than one solution |
• Task 2
• Describe methods for solving quadratic equations and share pros and cons for each method.
1 Factoring
Pros : quick and straightforward if the equation can be factored easily
Cons : not all quadratic equations can be easily factored if it is not straightforward.
2 Completing the square method
Pros: works for all kinds of quadratic equation and it can be used to derive the quadratic formula
Cons: it can be hard cumbersome and can take more time to get to the answer
3 Quadratic formula
Pros: there can be applied to any quadratic equation and it also provides exact solutions.
Cons: requires more calculation and can be complex and cumbersome when there is more more or large coefficient.
• Task 3
• Solve for linear equation 3x + 2 = 11 and show value of x?
• Solve for this quadratic equation x^2 + 2x - 6 = 0.
(You are required to solve these problems at paper and then share clear photographs for adding a touch of your creativity and personal effort which should be marked with your username)
• Task 4
Scenario number 1
Suppose Ali have $15 for spending at snacks. He is buying a pack of chips for $3. How much money he have left?
Suppose x is amount of money Ali has left.
Equation: x + 3 = 15
Share a solution for x
(Solve the above scenerio based questions and share step by step that how you reach to your final outcome)
Scenario number 2
Suppose there's a ball which is thrown in upward direction from ground with initial velocity of 20 m/s and height of ball above ground is presented by following equation;
h(t) = -5t^2 + 20t
Here h is height in meters and t is time in seconds.
Share about maximum height reached by this ball!
Please solve for h!
Now substitute back into the height equation to find the max height
So the height reached by the ball is 20 meters
Thanks for reading I will now like to call on @ruthjoe @ahansharif and @john247 to also take part in this learning challenge

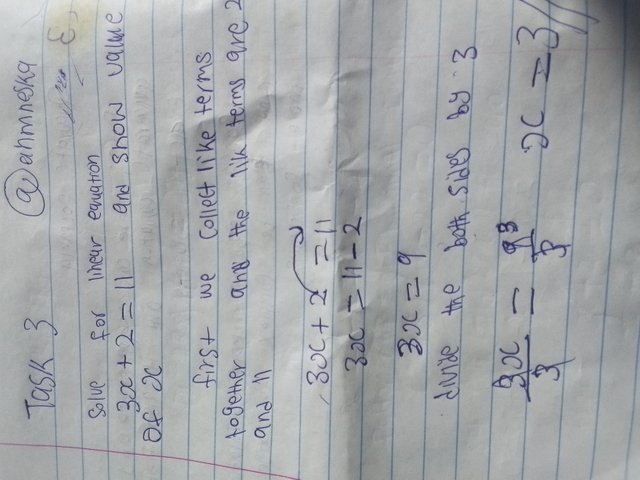



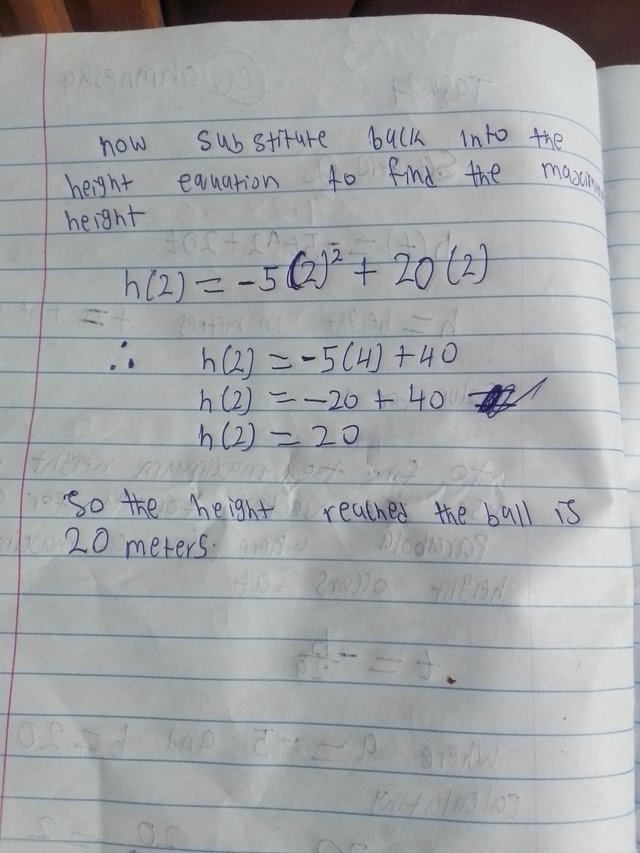
https://x.com/ahmneska/status/1878095025721995712?t=yPVHRyG0b6bVYE_55c2LCA&s=19