SLC S22W6//Graphing and Conic sections

_{Image taken from Pixabay}

Hello everyone. Today I will take part in week 6 of Steem Learning Challenge, by @khursheedanwar, based on polynomial and rational expressions. You can check it here SLC S22W6//Graphing and Conic sections.

So, let's get started.

Differentiate between quadratic and exponential functions with examples and general forms of each!

A quadratic function represents a polynomial function where the highest power of the variable is 2. The general form of this type is: f(x) = ax^2 + bx + c, where a, b and c are constants. The graph representation is a parabolic shape that can be opened upward or downward, based on the sign of a (negative or positive).
For example: f(x) = 2x^2 - 4x + 1 will open upwards as a = 2 > 0

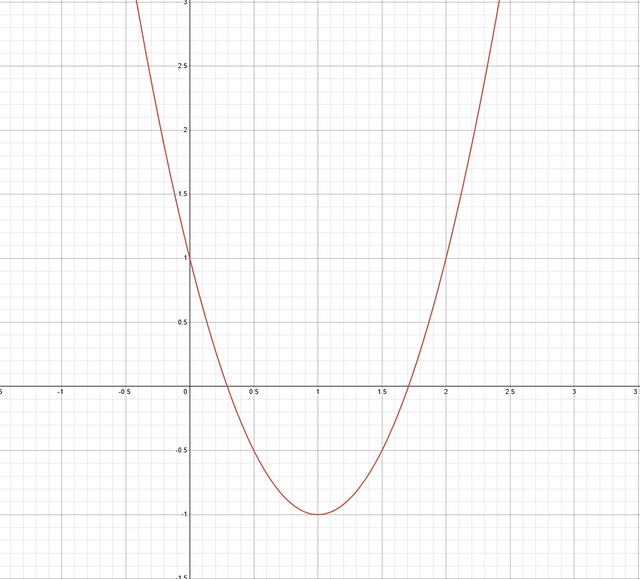
_{Parabola opening upwards}

We can find this type of function used in: finding the height of a ball, designing a rectangular yard and many other fields.

An exponential function has a constant base that is raised to a variable exponent. This type of function is characterized by rapid growth or decay, based on the base value. General form: f(x) = ab^x, where a is the initial value, b is the growth factor (if b > 1 growth, 0 < b < 1 for decay).
For example: f(x) = 3(2^x) which has an exponential growth as b = 2 > 1

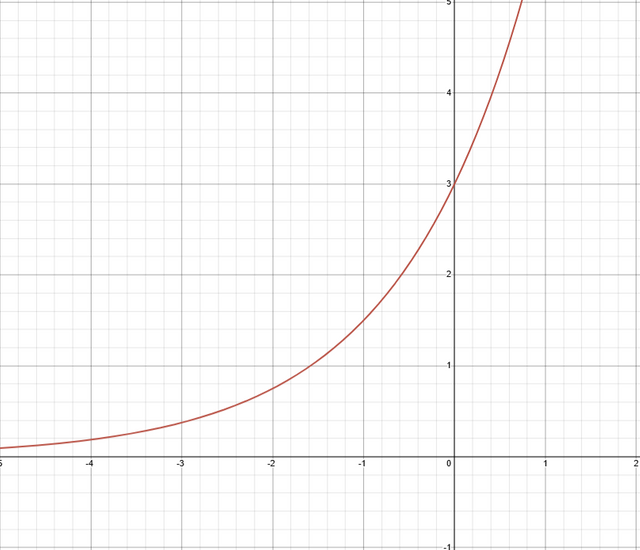
_{Exponential growth}

This type of function is used in: modeling population growth, radioactive decay

Feature	Quadratic Functions	Exponential Functions
General Form	f(x) = ax^2 + bx + c	f(x) = ab^2
Example	f(x) = 2x^2 - 4x + 1	f(x) = 3(2^x)
Graph	Parabola with opening based on value of a	Rapid growth or decay based on b
Uses	finding the height of a ball, designing a rectangular yard	population growth, radioactive decay

Provide real world examples of exponential functions and quadratic functions (Minimum 2 for each)that are not discussed in class!

Exponential functions

Radioactive decay
Radioactive substances decay over time and they lose mass or energy. The amount of substance left can be modeled as: M(t) = M₀e^-kt, where:

• M(t) - is the remaining mass after the time t
• M₀ - is the initial mass
• k - decay constant
• t - time
  If we consider a initial mass M₀ = 50g, the decay constant k = 0.1. After t = 5 years the mass will be:

M(t) = M0e^(-kt)
M(5) = 50e^(-0.1 * 5)
M(5) = 50e^(-0.5)
M(5) ~= 30.33 g

After 5 years, 30.33g of substance will be left.

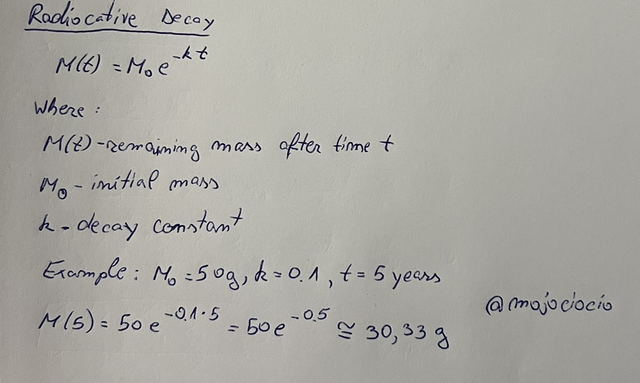
Population growth
Population can grow at an exponential rate if we have unlimited resources. We can model it like this: P(t) = P₀e^rt, where:

• P(0) - initial population
• r - growth rate
• t - time
• P(t) - population after time t
  Let's say we have a initial population of P(0) = 1000, growth rate r = 0.05. The population after t = 10 years will be:

P(10) = 1000e^(0.05 * 10)
P(10) = 1000e^(0.5)
P(10) ~= 1649

After 10 years, the population will be approximately 1649.

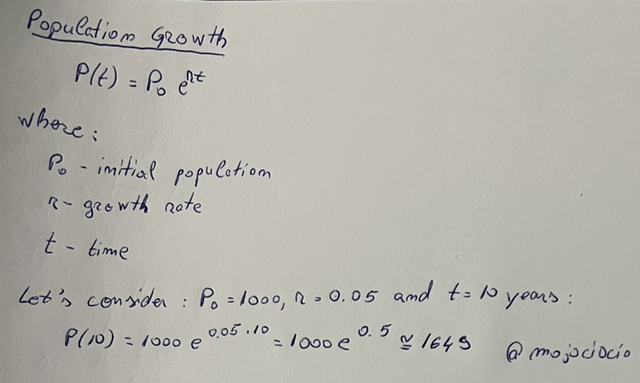
Quadratic functions

Revenue Optimization

Let's say a business wants to maximize it's revenue based on the price of the product. We can model it like this: R(x) = -ax^2 +bc + c, where: a is the coefficient that will give a downward opening to the parabola, b and c are parameters.

Let's take this example: R(x) = -2x^2 + 12x + 20, where x is the price.

We will have a maximum profit at the vertex: x = -b/2a. Solve for x: x = -12/2(-2) = 12/4 = 3.

Substitute x = 3 in the equation:

R(3) = -2(3)^2 + 12(3) + 20
R(3) = -2(9) + 36 + 20
R(3) = -18 + 36 + 20
R(3) = 38

The price needed to maximize the revenue is $3 and the maximum revenue is $38.

Motion of a Rocket

We can use quadratic functions to model the the motion of a rocket, the maximum height it will reach and after how much time it will return to ground.

Example: h(t) = -4.9t^2 + 100t where:
-4.9t^2 - effect of gravity on the rocket
100t - initial velocity of the rocket

The maximum height of the rocket can be found by calculating the vertex: t = -b/2a = -100/2(-4.9) ~= 10.2 seconds.

h(10.2) = -4.9(10.2)^2 + 100(10.2) = -4.9(104.04) + 100(10.2)
h(10.2) ~= 510.2 meters

The rocket will reach approximately 510.2 meters after about 10.2 seconds.

Now let's see when it will return to the ground. This happens when h(t) = 0.

-4.9^2 + 100t = 0
t(-4.9t + 100) = 0
t = 0 (start)
-4.9t + 100 = 0
t = 100/4.9
t~= 20.4 seconds

The rocket will return to the ground after 20.4 seconds.

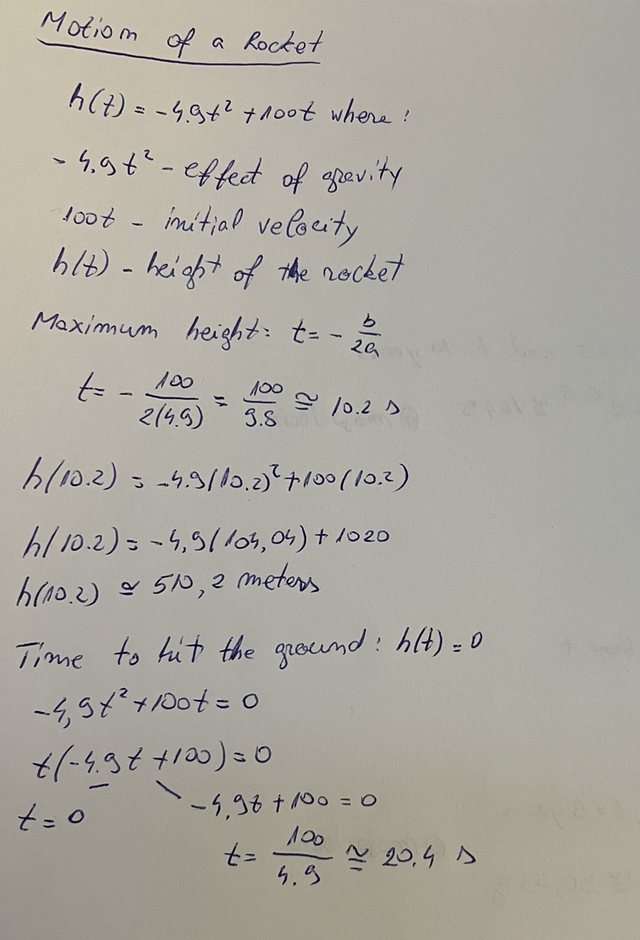
Please find out equation of the circle with center (2, 3) and radius 4.

To find the equation of a circle, we need to use the formula: (x - h)^2 + (y - k)^2 = r^2.
From the given information, we can identify:

• center: (h, k) = (2, 3)
  h = 2, k = 3
• radius r = 4

The steps to find the equation of the circle are:

• We introduce this into the formula and get: (x - 2)^2 + (y - 3)^2 = 4^2.
• Raise to power in both sides to obtain: x^2 -4x + 4 + y^2 - 6y + 9 = 16
• Group the constants to the right side and the variable terms in the left: x^2 -4x + y^2 - 6y = 16 - 4 - 9
• Perform the subtractions: x^2 -4x + y^2 - 6y = 3
• Write the final solution: x^2 -4x + y^2 - 6y - 3 = 0

Please solve for x: 2x^2 + 5x - 3 = 0

To solve the given equation, 2x^2 + 5x - 3 = 0, we will use the quadratic formula: x = (-b ± √(b^2 - 4ac)) / 2a. From the given equation, we can extract the needed information:

• a = 2
• b = 5
• c = -3
  If we replace this in the formula, we get: x = (-5 ± √(5^2 - 4(2)(-3))) / 2(2). By raising to power and performing the multiplications and additions we have: x = (-5 ± √49) / 4. This becomes: x = (-5 ± 7)/4.
• x₁ = (-5 + 7)/4 = 2/4 = 1/2
• x₂ = (-5 - 7)/4 = -12/4 = -3

The final solution is: x₁ = 1/2, x₂ = -3.

The parabola is open upwards, intersecting the x axis in -3 and 1/2.

Scenario number 1: Suppose there's a satellite dish which is shaped like paraboloid. If equation of the paraboloid is given by y = 0.1x^2 then here x and y are measured in meters so now;

a) You need for graphing this equation.
To plot the graph for the given equation y = 0.1x^2, we can give x some values and find the respective y:

• x = -5 => y = 0.1(-5)^2 = 0.1(25) = 2.5
• x = -3 => y = 0.1(-3)^2 = 0.1(9) = 0.9
• x = -1 => y = 0.1(-1)^2 = 0.1(1) = 0.1
• x = 5 => y = 0.1(5)^2 = 0.1(25) = 2.5
• x = 3 => y = 0.1(3)^2 = 0.1(9) = 0.9
• x = 1 => y = 0.1(1)^2 = 0.1(1) = 0.1

The vertex of the parabola is (0, 0). The graph can be seen below:

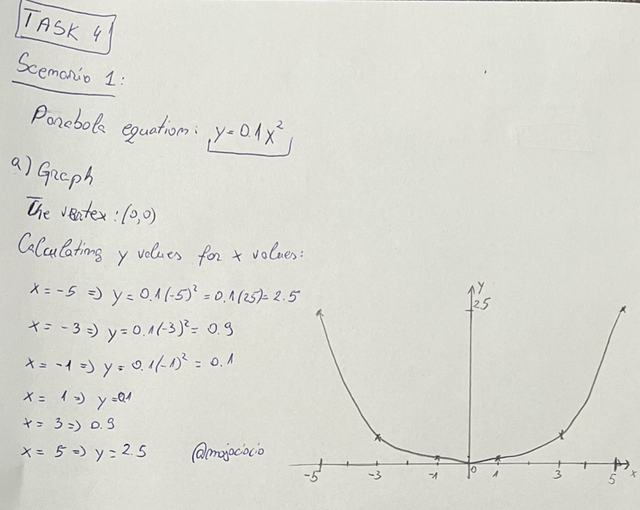
_{Graph of y = 0.1x^2}

b) You need for finding out focal length of paraboloid.

The general form of a parabola is: 4p(y - k) = (x - k)^2, where (h, k) - vertex.

From point a) we can say that the vertex is (0, 0) so h = 0, k = 0 which will give us the general parabola equation as: 4py = x^2.

I multiply the given equation y = 0.1x^2 by 10 and rewrite it as 10y = x^2, to help me in future calculations.

Now, we can substitute x^2 in the general equation of the parabola to find p: 4py = 10y. Dividing this by y, we have: 4p = 10.

Doing the calculation, we get: p = 10/4 = 2.5 meters.

The focal length of the parabola is 2.5 meters.

c) You need for finding out equation of directrix.

In case of a upward opened parabola, the directrix is a horizontal line that is located p units below the vertex, y = -p.

Since we know that p = 2.5 from the previous point, we can say that:
Directrix y = -2.5.

Scenario number 2: You need for suppose that there's a ball which is thrown in upward direction from ground with an initial velocity of 50 ft/s. Suppose if height of ball above ground is given by the equation h(t) = -16t^2 + 50t and here t is presenting time in seconds then;

a) You need for graphing this equation.

Based on the given equation h(t) = -16t^2 + 50t, where a = -16 and b = 50 we can say that we have a downward opened parabola.

If we give some values to t, we can plot the graph:

• t = 0 => h(0) = 0
• t = 1 => h(1) = -16(1)^2 + 50(1) = 34
• t = 1.5 => h(1.5) = -16(1.5)^2 + 50(1.5) = 28
• t = 2 => h(2) = -16(2)^2 + 50(2) = 32
• t = 2.5 => h(2.5) = -16(2.5)^2 + 50(2.5) = 18

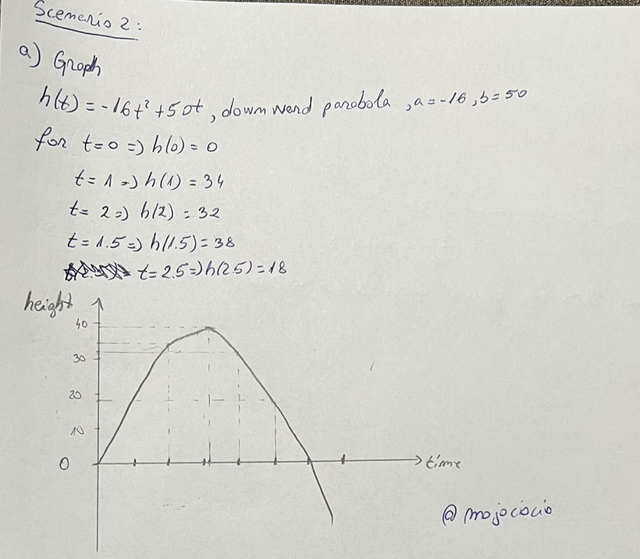
b) You need for finding out maximum height reached by this ball.

The maximum height of the ball is at the vertex of the parabola: t = -b/2a,where a = -16 and b = 50. Substituting the values in the formula we have:
t = -50/2(-16); t = 1.5625 seconds

Now we substitute t = 1.5625 in the equation to find the height:

h(1.5625) = -16(1.5625)^2 + 50(1.5625) = -16(2.4414) + 78.125 = -39.0625 + 78.125
h(1.5625) = 39.0625 feet

The maximum height reached by the ball is 39.0625 feet after 1.5625 seconds

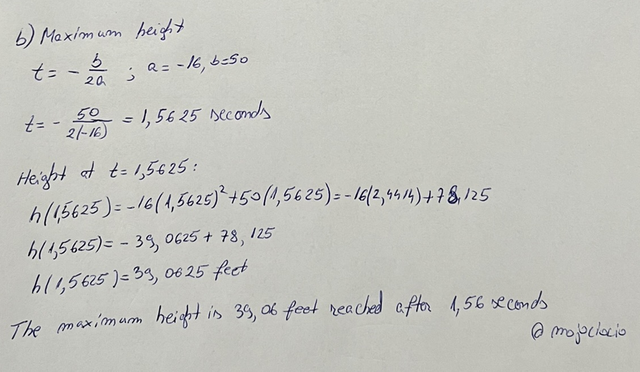
c) You need for finding out time which it is taking for ball for reach to ground.

The ball hits the ground when h(t) = 0.

-16t^2 + 50t = 0
t(-16t + 50) = 0

t = 0 - moment of throw

-16t + 50 = 0
t = 50/16
t = 3.125 seconds - return to ground

The ball will return to the ground after 3.125 seconds

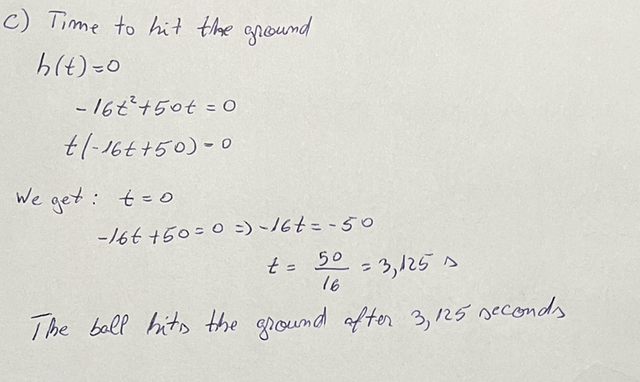
As always, thank you for reading and I'd like to extend an invitation to @ady-was-here, @radudangratian and @cmalescov to take part in this.