"SLC-S22W6//Graphing and conic sections."

Source

Task 1

• Differentiate between quadratic and exponential functions with examples and general forms of each!

Here I have differentiated between quadratic and exponential functions as requested by the professor.

Differences	Quadratic Functions	Exponential Functions
General Form	The general form is =ax^2 + bx + C, where a = 0	The general form is f(x) = a . b^x, where a > 0, b /> 0, and b = 1
Characteristics	Graph is a parabola (U-shaped), Growth is polynomial, not as rapid as exponential, Symmetry about the vertex, Positive a: Opens upwards; Negative a: Opens downwards.	Graph increases (or decreases) rapidly, Growth rate depends on the base b, No symmetry or vertex like Quadratics, Horizontal asymptote y = 0 for a > 0
Example	f(x) = 2x^2 + 3x - 5 , g(x) = -x^2 + 4x + 1	f(x) = 3 . 2^x , g(x) = 5 . (0.5)^x

---

Task 2

• Provide real-world examples of exponential functions and quadratic functions (Minimum 2 for each) that are not discussed in class!

Based on real-world examples of exponential functions and Quadratic Functions are as follows:

Exponential Functions

• Population Growth: A population doubling (increasing) every few years follows P(t) = P_0 . 2^t, where P_0 is gg initial population size and t is the time. Example New York City's population grows from 2000 to 4000 in 3 years.

• Compound Interest: The interest that is earned on a principal amount compounded annually follows A(t) = P . (1 + r)^t where r is the interest rate. Example My savings account earning is 5% interest annually.

Quadratic Functions

• Projectile Motion: An object thrown upward follows h(t) = - 16t^2 + v_0t + h_0, where v_0 is the initial velocity and h_0 is the initial height. Example A ball is thrown upward with an initial velocity of 20 m/s.

• Revenue Optimization: A company's may follow R(x) = -x^2 + 20x + 50, where x is the number of products that is sold. Example Determining the price that maximizes revenue for a product.

---

• Task 3

Please find out the equation of the circle with center (2, 3) and radius 4.

Please solve for x: 2x^2 + 5x - 3 = 0

Task 4

Scenario number 1

Based on the given equation: y = 0.1x^2

The equation represents a parabola that opens upward, with the vertex at the origin 0, 0. Now let's solve each of the parts step by step.

a) Graphing the Equation

• To graph the parabola, we need to calculate y values for specific x values.

• We will need to use a range of x values to compute corresponding y values:

x	y = 0.1x^2
-4	0.1(-4)^2 = 1.6
-3	0.1(-3)^2 = 0.9
-2	0.1(-2)^2 = 0.4
-1	0.1(-1)^2 = 0.1
0	0.1(0)^2 = 0
1	0.1(1)^2 = 0.1
2	0.1(2)^2 = 0.4
3	0.1(3)^2 = 0.9
4	0.1(4)^2 = 1.6

• We have to plot these points: (-4, 1.6), (-3, 0.9), ..., (4, 1.6).

• Draw a smooth U-shaped curve passing through these points.

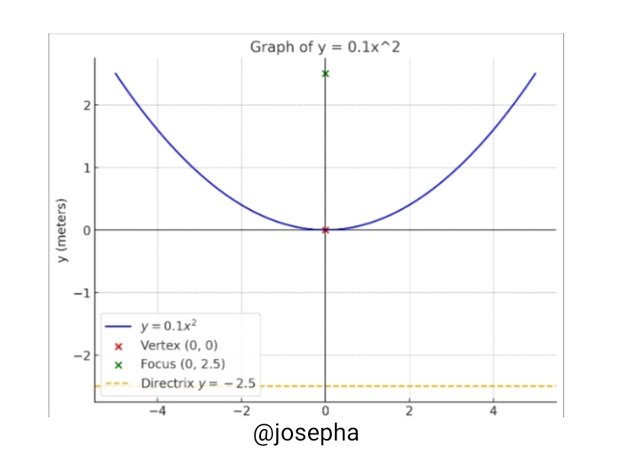
Here, we have our graph of the parabola y = 0.1x^2:

• In the above graph, the vertex at (0, 0) is the red point.

• The focus at (0, 2.5) is the green point.

• The Directrix at yb= - 2.5 is the orange dash line.

b) Finding the Focal Length

The standard or a parabola that opens upward is: y = 1/4p x^2

• Here, P stands as the distance from the vertex to the focus.

• Compare the given equation y = 0.1x^2 with y = 1/4p x^2

1/4p = 0.1

Solve for P:

4p = 1/0.1 = 10 ⇒ p = 10/4 = 2.5
Final Length: p = 2.5 Meters

C) Finding the Equation of the Directrix

The Directrix of a parabola is a horizontal line located at a distance p below the vertex.

Now since the vertex is at (0, 0) and (p = 2.5):

y = - 2.5
Equation of the Directrix:
y = - 2.5

---

Scenario number 2

Ball Thrown Upward

Based on the given equation:

h(t) = - 16t^2 + 50t

Where:

• h(t) Is the height of the ball in feet.
• t is the time in seconds.

a) Graphing the Equation

For to graph, we will need to calculate the height h(t) at different times t:

• Find critical points (intercepts, vertex):
  intercepts, the start of of the ball at t = 0 and returns to the ground when h(t) = 0. This will be calculated later. Vertex, the maximum height occurs at the vertex.

• Computer values for h(t):

(t) (seconds)	(h(t) = -16t^2 + 50t) (feet)
0	0
1	-16(1)^2 + 50(1) = 34
2	-16(2)^2 + 50(2) = 36
3	-16(3)^2 + 50(3) = -18

Based on the above, it means the ball reaches the ground again just after t = 3.

b) Finding the Maximum Height

The vertex of a quadratic equation h(t) = at^2 + bt + c is given by:

t = -b/2a
Here, a = -16, b = 50, c = 0.
t = -50/2(-16) = 50/32 = 1.5625 seconds.
Substitute t = 1.5625 into h(t) to find the maximum height:
h(1.5625 = -16(1.5625)^2 + 50(1.5625)
h(1.5625) = -16(2.4414) + 78.125 = -39.0625 + 78.125 = 39.0625 feet
Maximum Height:
39.0625, feet at t = 1.5625 seconds.

c) Finding the Time to Reach the Ground

The ball reaches the ground when h(t) = 0:

-16t^2 + 50t = 0
Factorize:
t(-16t + 50) = 0
This gives us two solutions:
t = 0 (Initial throw) or t = 50/16 = 3.125 seconds.

Timeto Reach the Ground:

3.125, seconds

a) Graph of the Height Function**

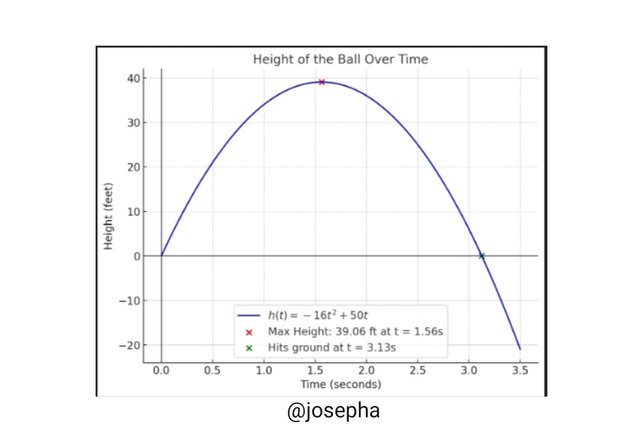
Here I plot the graph of h(t) = - 16t^2 + 50t

Looking at the graph it is the height function h(t) = - 16t^2 + 50t:

• The blue represents the trajectory of the ball.

• The red point represents the maximum height of 39.06 feet, which reached at t 1.56 seconds.

• The green represents when the ball hits the ground at t = 3.13 seconds.

I am inviting; @dove11, @lhorgic, and @ruthjoe

Cc:
@khursheedanwar