SLC S22W6//Graphing and Conic sections
Hello friends how are you doing today I am here to take part in the challenge that is quite informative and challenging.
Differentiate between quadratic and exponential functions with examples and general forms of each!
I will try to explain few differentiation between quadratic and exponential functions, with suitable examples and general forms as well.
If we see quadratic Function with General Form
I will explain the easy general form of a quadratic function is as follows.
f(x) = ax^1 + bx + c
where:
The constants are - a, b, and c and in case of
- a ≠ 0 (if a = 0, it's a linear function as well.
Example is as described
f(x) = 4x^1 + 2x - 3
Few characteristics are as follows.
The quadratic functions
It's in parabolic shape which may be u-shaped or inverted U-shaped.
There is single vertex
The presence of symmetry at vertical axis
The upward or downward graph 📉 📈 is present
Exponential Functions
Here is general form of exponential function
If f(x) = ab^x in this case constants are - a and b hence
- b > 0 and b ≠ 1 (if b = 1, it's called linear function
Example
f(x) = 4^x
Few characteristics are as follows.
Exponential functions are given below.
There is rapid increase or decrease in value as the value of x is changed.
There is horizontal asymptote in more simply it means the graph touching the horizontal line)
There is no vertex nor axis of symmetry
There is always positive positive
Task 2
I will try to explain examples from daily life for more easy understanding.
First of all I will explain the exponential Functions with examples.
If we see the virus Growth: the growth of virus can be just doubled in number within every few hours. If we have 10 virus initially, then the number of x hours would be modeled with the exponential function.
The second example is the Investment Growth: If I have invested $100 having a 5% annual interest rate, my investment will grow exponentially with over time.
Now Quadratic Functions
For example if I am Throwing a Ball in upward direction it's upwards height will have quadratic path, the ball would move up, peaked and obviously then come back.
Then I would like to Designing a Garden in case I have rectangular garden having fixed amount of fence I will use quadratic function to finding optimal numbers of dimensions.
Task 3
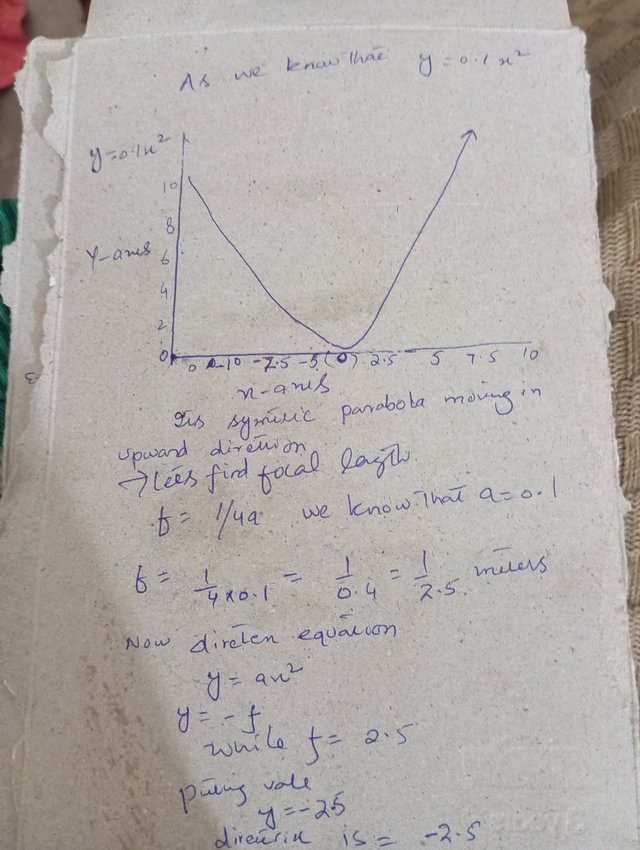
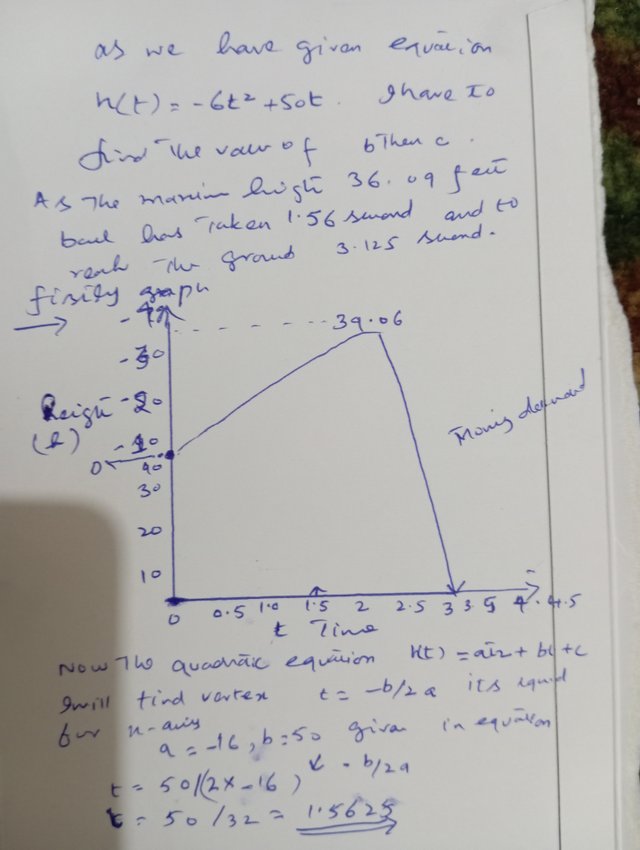
 |  |
|---|
Task 4
Scenario 1
Scenario 2
It's all about my today's post.
I would like to invite my friends @m-fdo, @jannat12 and @iqrarana786 to take part in the challenge.


@tipu curate
Upvoted 👌 (Mana: 7/8) Get profit votes with @tipU :)