"SLC-S22W6//Graphing and conic sections."

• Task 1

• Differentiate between quadratic and exponential functions with examples and general forms of each

Quadratic and exponential functions are tools within algebra that are fundamental in other branches of mathematics and have a wide variety of applications in real life, science, engineering and medicine.

I really congratulate Professor @khursheedanwar for choosing this very fundamental topic within algebra.

Let's look at some algebraic examples and their respective graphs to better visualize their behavior:

Quadratic Functions

• General form: f(x) = ax² + bx + c, where a, b and c are constants.
• Graph: A parable.

Examples:

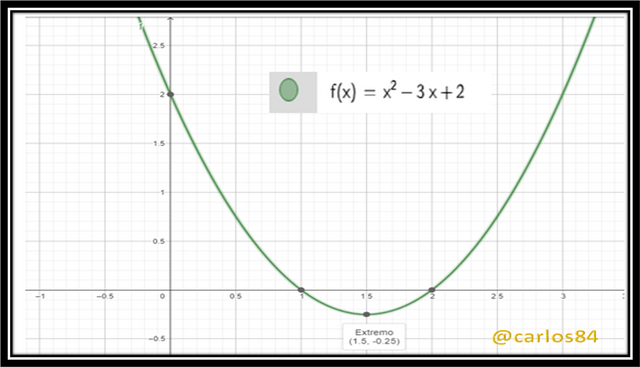
• f(x) = x² - 3x + 2

We find the vertex, finding f'(x) = 0, which implies that:

f'(x) = 2x -3
2x-3 = 0
x = 3/2
x = 1.5, this value is substituted into f(x)

f(3/2) = (3/2)² - 3(3/2) + 2
f(3/2) = 9/4 - 9/2 + 2
f(3/2) = -1/4
(f(3/2) = -0.25

The coordinates of the vertex point are: (3/2 ; -1/4)

• Intercept with x-axis if y=0

x² - 3x + 2 = 0

We factor the second degree equation:(x - 1) (x - 2) = 0

X1= 1
X2 = 2

Graphing in GeoGebra:

• Applications of the quadratic function in physics: Taking into consideration that the geometry of a quadratic function is a parabola, then we can say that the trajectory that an object follows when it is launched as a projectile follows the shape of a parabola, also from a geometric point of view a parabola is the projection in the plane of a parabolic antenna.

• Applications of the quadratic function in engineering: the design of bridges, the construction of arches, which leads us to conclude that the study of the parabola is very important in civil engineering and construction.

• Applications of the quadratic function in economics: supply and demand models, profit maximization, since many of the curves constructed in economics follow the path of a parabola.

Exponential functions

• General form: f(x) = a·b^x, where a and b are constants and b > 0, b ≠ 1.

• Graph: An exponentially increasing or decreasing curve.

Examples:

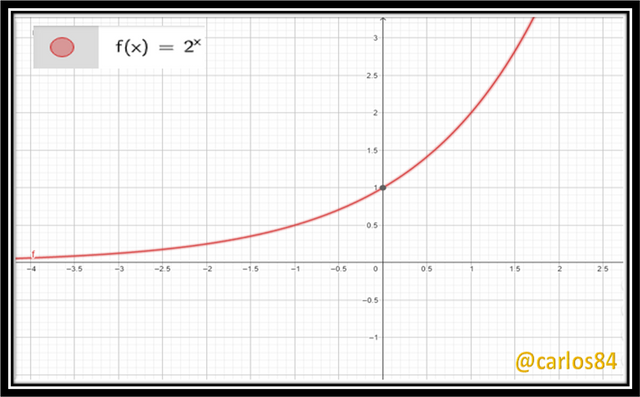
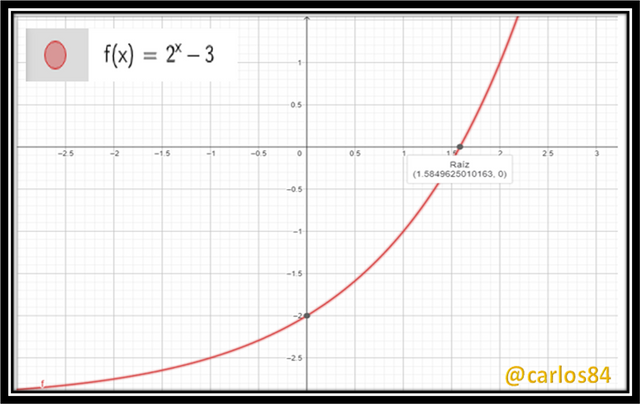
• f(x) = 2^x

This is a type of function that will almost always cut the Y axis at y = 1, since when we do x = 0 we will have a^0, which implies that every number or variable raised to the zero power is equal to one, that is a^0 = 1 .

Another characteristic is that it will not cut with the x-axis, the reason is that to find the cut with the x-axis, you have to make f(x) = 0, at the same time Natural Logarithm (Ln) is applied to both sides of the equality, example:

2^x = 0

There is a property of natural logarithm (Ln) that states:

Ln (a^n) = n Ln (a)

Then we can apply natural logarithm to both sides of the equality:
Ln (2^x) = Ln(0)

x Ln (2) = It does not exist.

The natural logarithm (Ln) of zero does not exist because it tends to be infinite, which means that the basic function f(x) = a^x does not cut the x-axis, on the contrary the x-axis ends up being a horizontal asymptote for this type of function.

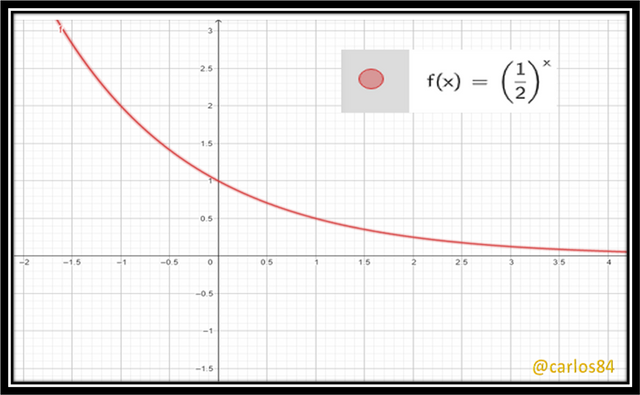
Let's look at the GeoGebra graphics of two examples:

[1] f(x) = 2^x

[2] f(x) = (1/2)^x

With the two graphs we can conclude that the graph of basic exponential functions of the type f(x)= a^x cut the y-axis at y=1, the x-axis is a horizontal asymptote.

The only difference in the two examples of exponential functions is that f(x)= 2^x grows when x tends to infinity, while f(x) = (1/2)^x decreases when x tends to infinity, which makes us conclude that this type of basic exponential function f(x) = a^x grows or decreases when x tends to infinity depending on the value of a.

Although the basic exponential function f(x) = a^x does not cut the x-axis, the vertically translated exponential function does, depending on the value of the addition or subtraction, for example:

[3] f(x)= 2^x -3

Adding or subtracting a real number to the basic exponential function f(x) = a^x can cause it to cut off the x-axis, and the y-axis can cut it off at a value other than 1.

Applications of the exponential function

In biology, it is possible to estimate the growth of populations of bacteria, viruses or any type of microorganism, since the growth of many of these microorganisms follows the behavior of this type of function.

In economics and finance there are concepts that follow the behavior of the exponential function, as is the case of compound interest and the depreciation of real estate.

Comparison between both functions:

Feature	Quadratic Function	Exponential Function
General form	ax² + bx + c	a·b^x
Graph	Parable	Exponential curve
Exchange rate	Varies linearly	Proportional to present value
Applications	Trajectories, areas, optimization	Rapid growth/decrease, natural phenomena

In summary, I can say that quadratic functions can describe various physical phenomena where particularly there is a linear rate of change, an example of this is the launching of a projectile or the deflection of a beam. Exponential functions can simulate the behavior of phenomena where there are very rapid growth or decay processes, exponential functions also simulate very well the behavior of population growth.### • Task 2

• Provide real world examples of exponential functions and quadratic functions (Minimum 2 for each)that are not discussed in class!

Real-world application of the quadratic function in economics.

Revenues of a company: In some cases, a company's revenues can be modeled as a quadratic function, where there is an optimal point of production that maximizes profits.

Demand for a product: The relationship between the price of a product and the quantity demanded can follow a parabola-shaped curve, especially when there is an optimal price that maximizes revenue.

Example

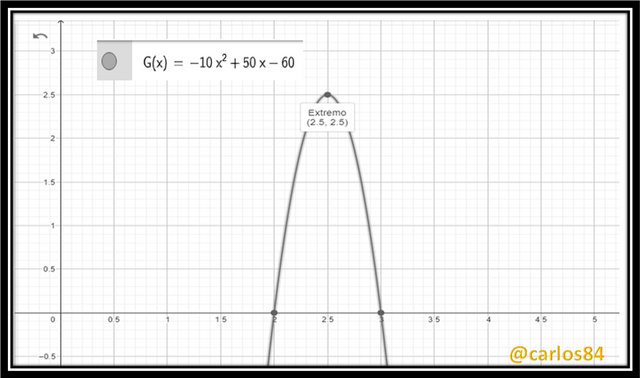
A company that manufactures and sells sports jerseys has determined that its daily profit (G), in dollars, is given by the function G(x) = -10x² + 50x - 60, where x represents the number of jerseys sold in a day.

We ask:

• How many T-shirts must the firm sell to maximize its daily profit?
• What is the maximum profit the firm can make in a day?

Analysis:

This problem is modeled with a quadratic function, where the maximum gain is at the vertex of the parabola.

Solution:

[1.] Find the vertex:

• The x-coordinate of the vertex will give us the number of shirts that maximize the profit. The formula to find the x-coordinate of the vertex is: x = -b / 2a.

• In this case, a = -10 and b = 50.

Substituting: x = -(50) / (2 * -10)

x= -50 / -20

x = 2.5

We can also plot the parabola, and where the vertex is, that will be the value of the maximum sale:

G(x) = -10x² + 50x - 60

From the graph we can also verify that the maximum profit value is 2.5 dollars.

1. Calculate the maximum gain:

• We substitute the value of x =2.5 into the gain function: G(x)

G(2.5) = -10(2.5)² + 50(2.5) - 60

G(2.5) = -62.5 + 125 -60

G(x) = 125 - 122.5

G(x) = 2.5 dólares

The firm must sell 2.5 T-shirts to maximize its daily profit.

The maximum profit the company can make in a day is $2.5.

This exercise demonstrates how quadratic functions can be used to model real situations, such as profit maximization in a company. In this case, the parabola represents the relationship between the number of T-shirts sold and the profit earned, and the vertex of the parabola indicates the maximum profit point.

Real-world application of the quadratic function in Biology

The growth of a plant can be affected by multiple biological factors, in many cases the growth of a plant follows the behavior of a quadratic function, I will explain the following example:

A farmer observes that the height of his corn plants increases rapidly at first, but then stabilizes. After several experiments, he discovers that the height of the plants (in centimeters), as a function of the number of weeks since planting (x), can be modeled by the function:

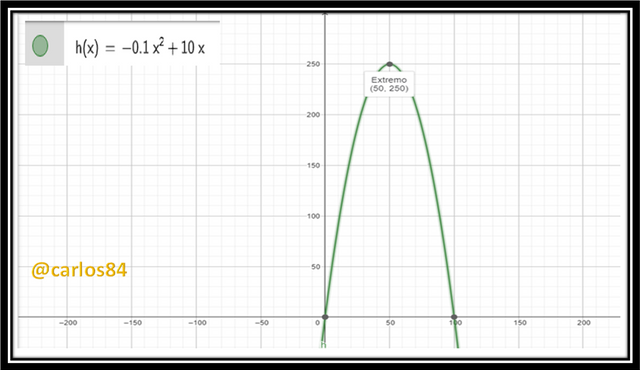
• h(x) = -0.1x² + 10x

Requested:

• What is the maximum height that corn plants reach?
• After how many weeks this maximum height is reached?
• What does the independent term (0) in this function mean? - What does the independent term (0) in this function mean?

Analysis:

This quadratic function represents a parabola that opens downward, indicating that plant growth increases until it reaches a maximum and then decreases. The vertex of this parabola will represent the maximum point of growth.

Solution:

[1.] Maximum height:

• The maximum value of a quadratic function is at its vertex. To find the y-coordinate of the vertex, which represents the maximum height, we use the formula: y = c - (b^2 / 4a), where a, b and c are the coefficients of the quadratic equation.

• In this case, a = -0.1, b = 10 and c = 0. Substituting: y = 0 - (10^2 / 4 * -0.1) = 250.

• The maximum height of the plants is 250 centimeters.*

We can plot the function h(x) = -0.1x² + 10x with GeoGebra software and observe the Y-coordinate of the vertex, and that value will be the maximum growth value of the plant:

In the graph it can be clearly observed that the value of the Y coordinate is 250, therefore the maximum growth of the plant was 250 centimeters.

[2]Time to reach the maximum height:

The x-coordinate of the vertex tells us at what time the maximum height is reached. The formula for the x-coordinate of the vertex is: x = -b / 2a.

• Substituting the values: x = -10 / (2 * -0.1) = 50.

• The plants reach their maximum height after 50 weeks *

We can verify from the graph of the function h(x) = -0.1x² + 10x that the time to reach the maximum height of 250 centimeters is actually 50 weeks.

It is clear that the X-coordinate of the vertex is 50, therefore the time to reach the maximum height of the plant is 50 weeks.

[3.] Meaning of the term independent:

• The independent term (0 in this case) represents the initial plant height. In this model, plants are assumed to be planted at ground level, so their initial height is 0.

Interpretation:

This exercise shows how quadratic functions can be used to model biological phenomena, such as plant growth. In this case, the quadratic function allows us to predict the maximum height the plants will reach and the time it will take to reach it.

Real-world application of the exponential function in Biology

• Bacterial growth: The number of bacteria in a colony can increase exponentially under ideal conditions, doubling at regular intervals.

Below is an exercise that serves as an example for this application to biology:

A colony of bacteria doubles every hour. If initially there are 100 bacteria, how many will there be after 2 hours?.

• Solution:

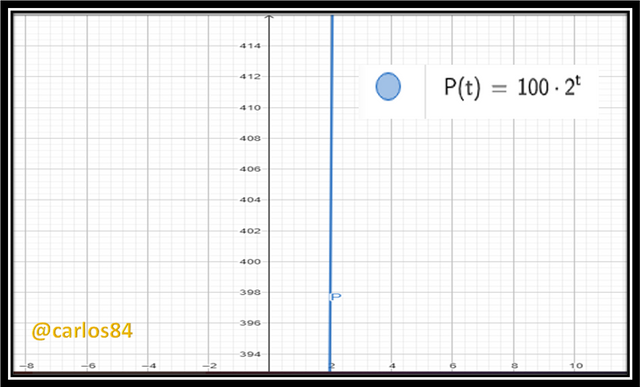
  • The exponential function that models this growth is: P(t) = 100 * 2^t, where P(t) is the population of bacteria at time t (in hours).

• To find the population after 2 hours, we substitute t for 2: P(2) = 100 * 2^2.

  • We calculate and obtain the result.

P(2)= 100 (2)^2

P(2) = 100 (4)= 400 bacteria, which means that after 2 hours of propagation there will be a total of 400 bacteria.

We can verify this result by graphing the exponential function in GeoGebra:

P(t) = 100 * 2^t

We can also analyze that at time t=0 there is already a proliferation of 100 bacteria, since

P(0) = 100 * 2^0
P(0)=100*1
P(0) = 100

Which corroborates that initially there are the 100 bacteria that are proliferating and doubling every hour.

Real-world application of the exponential function in Chemistry

Radioactive decay: This type of chemical reaction disintegrates exponentially, so when a radioactive isotope disintegrates it does so following the behavior of an exponential function, as explained in the following example:

A radioactive isotope has a half-life of 5 years. If we initially have 100 grams of this isotope, how many grams will be left after 15 years?

• Solution:

  • The exponential function modeling radioactive decay is: A(t) = 100 * (1/2)^(t/h), where A(t) is the amount remaining at time t, A₀ is the initial amount, h is the half-life, and t is the elapsed time.

  • We substitute the values in the formula: A(15) = 100 * (1/2)^(15/5).

• We calculate and obtain the remaining amount.

A(15) = 100 * 32773 / 5
A(15) = 655460 grams.

This means that only 655460 grams of the radioactive isotope, or 655.46 kilograms, remain in the decay process.

• Task 3

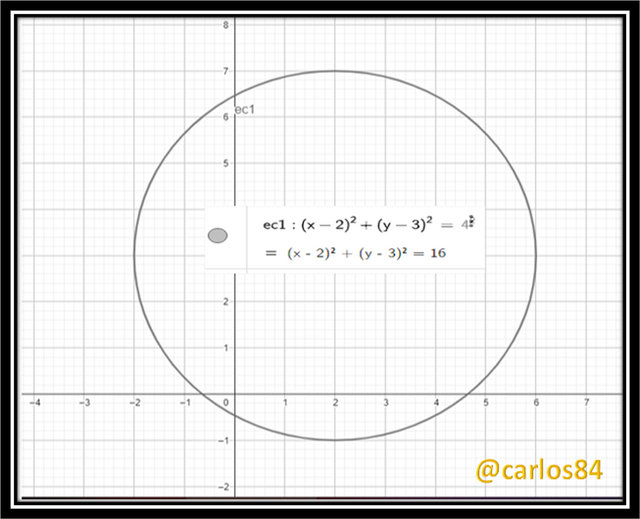
• Please find out equation of the circle with center (2, 3) and radius 4.

Circle graph with GeoGebra software:

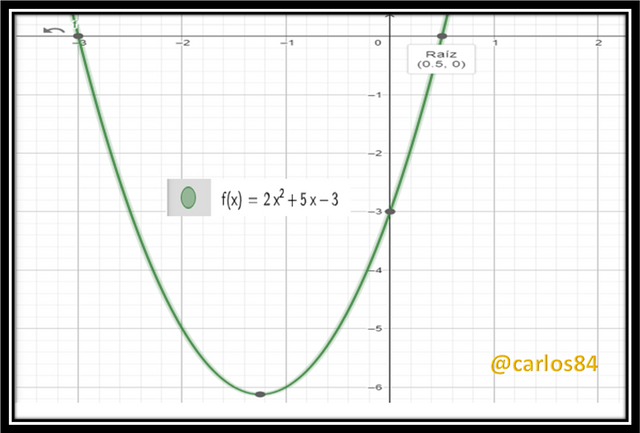
• Please solve for x: 2x^2 + 5x - 3 = 0

If we assume that this second degree equation is a function f(x) = 2x^2 + 5x - 3 we can graph it using GeoGebra software and where it cuts the x-axis will be the solution for x:

The parabola representing the function f(x) = 2x^2 + 5x - 3 has vertex coordinates at (-1.25 ; -6.125) and cuts the x-axis at X1= -3 and X2= 0.5 which is the solution of x of the equation: 2x^2 + 5x - 3.

• Task 4

Scenario number 1

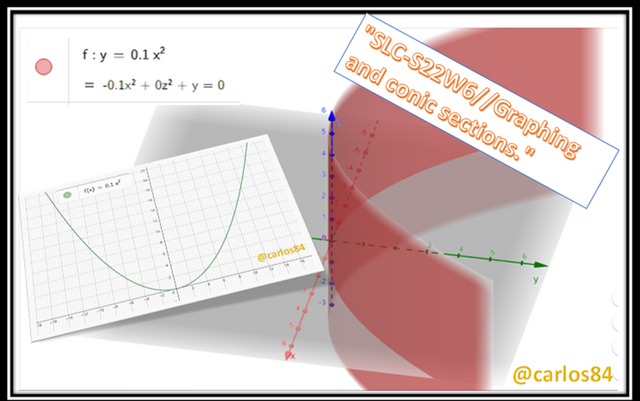
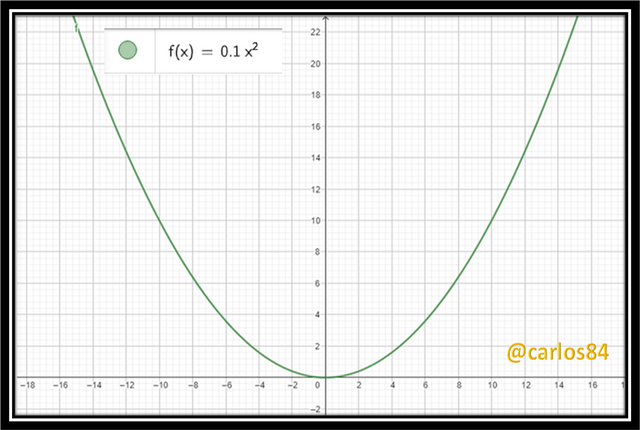
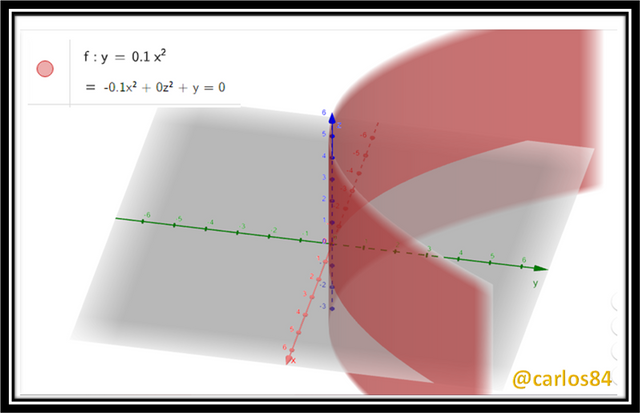
Suppose there's a satellite dish which is shaped like paraboloid.If equation of the paraboloid is given by y = 0.1x^2 then here x and y are measured in meters so now;

a) You need for graphing this equation.

As it represents a paraboloid it is important that the graph is expressed in 3 dimensions:

b) You need for finding out focal length of paraboloid.

To find the focal length of a paraboloid given by an equation, we need to compare its shape with the standard form of the equation of a parabola.

Standard form of an upward-opening parabola:
4p(y-k) = (x-h)²

Where:

• (h,k) are the coordinates of the vertex
• p is the focal distance

Comparing with our equation:
y = 0.1x²

We can rewrite it as:

4p(y-0) = (x-0)²

4py = x²

As y= 0.1 x

Implies that:

4p ( 0.1x) = x²

Multiply 4p * 0.1 x:

0.4px = x²

Clearance 0.4 p

0.4p = x²/x

0.4p = x

p = 1 / 0.4

p= 2.5 metros.

What does focal length mean?

The focal length represents the distance from the vertex of the parabola to its focus. In the case of a parabolic antenna, the focus is the point where all the parallel rays incident on the parabola are concentrated.

Perhaps if the vertex of the paraboloid were not at (0;0), the distance from its focus would be greater.

The focal length is an important characteristic of a parabola, since it determines its shape and optical properties. In the case of the parabolic antenna we are analyzing, a focal length of 2.5 meters indicates that the focus is 2.5 meters from the vertex of the parabola.

c) You need for finding out equation of directrix.

To find the direction of the directrix of a paraboloid, we must first understand what the directrix is and how it relates to the equation of the parabola.

What is the directrix?

The directrix of a parabola is a straight line perpendicular to the axis of symmetry of the parabola, such that the distance from any point on the parabola to the directrix is equal to its distance to the focus.

Finding the directrix:

Identify the standard form:

The standard equation of a parabola that opens upward is: 4p(y-k) = (x-h)²

Where:

*(h,k) are the coordinates of the vertex

• p is the focal length

Compare with our equation:
y = 0.1x².

Since the parabola opens upward, the directrix will be a horizontal line located at a distance p below the vertex.

The vertex is (0,0), so the directrix will be the line y = -p.

Substituting the value of p, we obtain that the equation of the directrix is y = -2.5.

This means that the directrix of the paraboloid y = 0.1x² is a horizontal line located at a distance of 2.5 meters below the x-axis.