Hello friends, I hope everyone is well? Alhamdulillah I am fine.
I am @sheikhtuhin
From #Bangladesh

Dear friends, today I am going to join SLC S22W4//Linear and Quadratic equations.This learning challenge is organized by the beloved teacher of this platform, @khursheedanwar Sir.I am very grateful to Sir because now I don't need to practice Maths. I have forgotten it for a long time, but thanks to Sir's arrangement, I am able to try those old topics again.

Without further ado, I'll start today's homework right away.

Difference between linear equation and quadratic equation:

Linear equation	Quadratic equation
🔲 A linear equation is a mathematical equation in which the power of the variable is at most 1.	🔲A quadratic equation is an equation where the highest power of the variable is 2.
🔲General form= ax+b=0 Where, a & b are real numbers and a≠0, X is a variable.	🔲 Its general form = ax²+bx+c=0 where, a,b & c are real numbers and a≠0, X is a variable.
🔲This usually indicates a straight line.	🔲This usually indicates a parabola.
🔲For example: Linear equation in one variable=2x+5=0, Solution: 𝑥 =−5/2	🔲 For example: Quadratic equation in one variable= x²−5x+6=0,Solution: x=2 and x=3 (Solved using the factoring method)
🔲The linear equation in two variables =3x+4y=12,It expresses the relationship between x and y and it represents a straight line.	🔲 Quadratic equation in two variables:=x²+y²=16,This indicates the equation of a circle.
🔲Linear equations are commonly used to solve real-life problems, such as:Calculating business profits,Determining speed or distance,Budget calculations.	🔲The quadratic equation is used in various places and situations in nature, such as:In the process of throwing objects ,In engineering design and implementation,In electronic circuit design
🔲The graph of a linear equation in one variable is a point & A linear equation in two or more variables represents a straight line. Example: y=2x+1 represents a straight line where the slope is 2.	🔲The graph of a quadratic equation is a parabola.If a>0, the parabola opens upwards,If a<0, the parabola opens downwards.
🔲Graph of a linear equation in two variables:	🔲Graph of quadratic equation:

Methods for solving quadratic equations:

The following methods are followed to solve quadratic equations. I will mention these methods step by step along with their advantages and disadvantages, InshaAllah.

(i) Factoring method.
(ii) Complete square method.
(iii) Using mathematical formulas.
(iv) Graphical method.

Factoring method:

In this method, the equation is divided into the product of two drivers.Then, each part is solved by setting it equal to zero to find the value of the variable.

For example

If there is an equation,
X²-5x+6=0
=> x²-3x-2x+6=0
=> x(x-3) -2(x-3)=0
=> (x-3)(x-2)=0
Either,

x-3=0 or x-2=0
=> X= 3 , => x=2

Benefits,

• The easiest and fastest method is if the equation can be factored.
• It is easy to calculate by hand.

Difficulty,

• Equations are not always easy to factor.
• This method does not work if the solution is fractional or complex.

Complete square method:

This method involves converting the equation into a perfect square.

For example

If there is an equation,
X²+6x+5=0

Step-1 Preparing to complete the square.

   X²+6x+5=0

=> X²+6x= -5

Step-2 Add or subtract by squaring b/2.

Here, (ax²+bx+c=0) According to the equation, b=6.

So, (6/2)²
=> (3)²
=> 9 .
We get 9 by adding both passes of the equation processed in the first step.

 X²+6x+9= -5+9

=> X²+2.x.3+3² = 4
=> (x+3)² = 4

Step-3 The perfect square must be solved.

(x+3)² = 4

=> x+3 = √4
=> x+3 = ±2

Either,
x+3 = 2 or x+3= -2
=> x= 2-3, => x= -2-3
=> X = -1, => x= -5

Benefits,

• Applicable to every quadratic equation
• Suitable for graphical interpretation.

Difficulty,

• There are many steps that are time consuming.
• Calculations are difficult for complex equations.

Using mathematical formulas.

Formula,

If, ax²+bx+c=0, then the mathematical formula for the quadratic equation is:

X = -b ± ✓(b²-4ac) / 2a

For example,

                    X²-4x-5= 0 
                Here, 
                a=1 , b= -4, c=-5

Using formula:

X = -(-4)±✓(-4²)-4×1×(-5)/2×1
X= 4±✓36/2
X = 4±6/2

Either,

X= 4+6/2   or   x= 4-6/2

=>X = 10/2, => x= -2/2
=>X= 5, => x= -1

Benefits:

• Applicable to any quadratic equation.
• It is possible to find both real and complex roots.
• Fast and accurate method.

Difficulty,

• If the calculation is wrong, the solution may also be wrong.
• Using formulas for complex numbers is difficult.

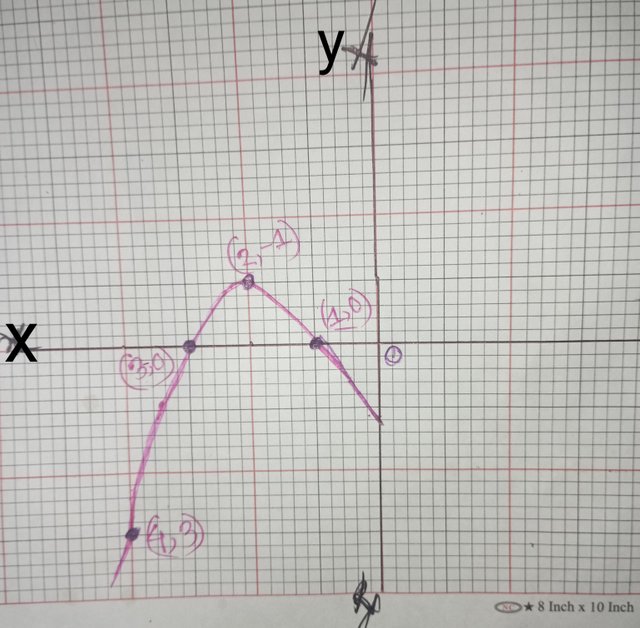
Graphical method.

The graph of the quadratic equation is drawn, and the point of intersection of the drawn line with the x-axis is determined.

For example:

Equation:
y= x²-4x+3

Graph x-axis intercept: x=1 and x=3

Benefits:

• A visual explanation of the solution is available.
• Useful for real-life problems.

Difficulty,

• Graph drawing requires time and precision.
• It is difficult to determine complex problems such as fractional solutions.

Comparative picture of the methods:

Opinion:

The method should be selected according to the type of equation and the requirement. Factoring methods are most useful for simple equations and mathematical formulas for complex equations. Graphical method can be used when visual explanation is needed.

Solution of linear equation:

Equation,
3x + 2 = 11

Step-1: The equation needs to be sorted over x.

   3x + 2 = 11

=> 3x+2-2=11-2

step-2: We divide both sides by three.

       3x=9
   => 3x/3 = 9/3
   => X = 3

Answer: (X = 3)

Solution for quadratic equation:

equation,
x² + 2x - 6 = 0

The formula for the quadratic equation is,

 ax²+bx+c=0

Then from the given equation,

   a=1
   b=2
   c= -6

Formula for solving quadratic equations:

X= -b±✓(b²-4ac)/2a

Solution Step-1: First, we need to determine the value of D.

    D= b²-4ac
    D= 2²-4×1(-6)
    D= 4+24
    D= 28

Step-2: Now let's put the values in the formula.

     X = -2±√28/2×1
     x= -2±√4.7/2
     x= -2 ± 2√7/2

Solution

    X1 = -2+2√7/2
          = 2(-1+√7)/2
          = -1+ √7


    X2 = -2-2√7/2
         = 2(-1-√7)/2
         = -1-√7

So, X1 = -1-√7 & X2 = -1-√7

solution

Ali has $15 for snacks. He bought a packet of chips for $3. We have to calculate how much money he will have left after buying the chips.

Let x be the amount of money left by Ali.
The equation is given by:

  x + 3 = 15

Now to find the value of x.

Step-1: We can arrange the equation for x.

   x+3=15

=> x+3-3= 15-3

step-2: Removes +3 and -3 from the left side

X+3-3=15-3

=>X=15-3

step-3 : By calculating 15-3 we get

  X= 15-3
=> x= 12

Final answer:

After buying chips from Ali, the remaining amount will be X = $12.

Remark:

If you try to solve this using simple unitary rules, it is possible to determine the answer very easily.

Where Ali has $15 and he will spend $3, naturally he will have $12 left.

Given information:

Equation:

h(t)=−5t² +20t

• h(t)= Height (in meters)
• t= Time (in seconds).

The maximum height of the ball needs to be determined.

Step 1: Determine the time of maximum altitude.

To find the value of
t at the vertex of the quadratic equation, we use the formula:

    t= -b/2a

Now,

 h(t)=−5t² +20t

In the equation
a= -5
b= 20

Now we can put the value in the formula.

  t= -b/2a
   t= -(20)/2.(-5)
   t= -20/-10
   t= 2

It will take t=2 seconds for the ball to reach its maximum height.

Step-2: Determine the height at t=2 seconds.

h(t)=−5t² +20t [Substitute t=2 in the equation.]

 h(2)=(−5)×(2)² +20×2
        = -20+40
        = 20

Answer: Maximum height h= 20 meters.