SLC-S22W4//Linear and Quadratic equations equations
.png) |
|---|
Dear steemian friends, this time I will take part in a valuable lesson with the theme “SLC-S22W4 //Linear and Quadratic equations equations”. To complete the requirements in this lesson, I would like to invite several other steemian friends to participate here, including bang @dove11 pak @muzack1 and @ulfatulrahmah.
Here is a simpler example of a linear equation and a quadratic equation to make it easier to understand:
- Linear Equation
The linear equation is one of the algebraic equations where the variable only has the highest rank of 1.
While the general form of the linear equation is as follows
ax+b=0
Let's look at one simple example of this linear equation:
x+2=0
Then the solution that we can do is :
x+2=0 (Move the number 2 to the right side of equal, so that the positive number 2 becomes negative)
x=−2
From this we know that there is only one value of x that satisfies the equation, which is x=−2
- Quadratic Equation
This quadratic equation is one of the algebraic equations which also has the highest power of 2 variables.
The most common form of quadratic equation can be seen as I shared below:
ax^2 + bx + c = 0
A simple example of a quadratic equation can be seen below:
x^2 - 3x + 2 = 0
Then the solution that we can do is:
Here I will factorize: x^2 - 3x + 2 = 0 to (x - 1)(x - 2) = 0. Now, this is how we know the value of x that completes: x = 1 or x = 2
It can be seen that there are two values of x that can complete the equation, namely x = 1 and x = 2.
| Differences in terms of | On Linear Equations | On Quadratic Equations |
|---|---|---|
| In terms of Highest Rank | 1 | 2 |
| In terms of Number of Solutions | 1 | 0, 1, or 2 |
| In terms of graphics | The graph is a straight line | The graph is Parabolic |
1. For the first one I used the Factorization Method
I did this method in the following way:
Here we will find two numbers that can equal the product of a constant and a sum equal to the coefficient x.
See the example below:
x^2 - 7x + 10 = 0
Find two numbers: -7 : -5 and -2
Factorize: (x-5)(x-2)=0
The result is : x=5 or x=2The advantage is :
If the equation can be factored, then we can find the result easily and quickly. Also, we don't need to spend a long time using tools like calculators.The disadvantages are:
This method does not always bring satisfactory results, especially if the roots of the equation used do not consist of rational numbers.
2. Next I used the Quadratic Formula method
How to do it:
The first step is to enter the values of a, b, and c into the formula. Then start by calculating the roots
See the example I gave below:
2x^2 - 4x : 6 = 0.
I entered it into the formula:
Discriminant : (-4)^2 – 4 (2) - (6) = 16 + 48 = 64
Do the math x :
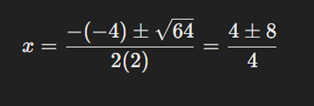
so, x = (4+8)/4 =3, or (4-8)/4 = -1
The result is: x = 3 or x = -1
The advantages are:
We can directly understand geometric relationships and easily find solutions including complex numbers.Disadvantages are:
It can take longer to find the correct result, and can be confusing if you don't practice.
3. The Graph method which I call the quite simple method
The trick is:
First need to draw the graph of the function y = ax^2 + bx + c. find the point of the graph that touches or that intersects the x-axis.
See the example below:
For x^2 +2x - 3 = 0, the graph intersects the x-axis at x = -3 and x = 1.
The solutions here are x = -3 and x = 1.
Advantages:
The most commonly used method that can find results with simple steps and is versatile.The disadvantage is that :
This method will lead to complicated steps and processes when the calculation coefficient is large. And it requires tools such as calculators to get root values that are not simple.
That is my participation in this algebra lesson. thank you very much to our teacher Mr. @khursheedanwar for giving this lesson, and to all friends who have stopped by my post. Greetings @cymolan


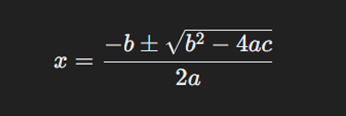






https://x.com/SaifulMaul41608/status/1877791592897191957
Anak muda bertalenta matematik ok semoga sukses buat postingan ini ananda cymolan