SLC S22W3//Equations and Systems of equations
Explain difference between linear and non linear systems of equations. Provide examples of each type of system of equation and describe their general forms.
If we study in math linear and nonlinear system for equation are integral components especially in case of Algebra. Hence the fundamentals difference is solving both equations.
Linear Systems of Equations
The collection of two or more than two linear equations that are showing variable. Hence in case case the power of variable should be 1.
There is an example.
General Form
A1x + B1y = C1
A2x + B2y = C2
Here we can see that A, B and C are constant while x, y and z are variables.
Let us study an Algeriac equation for more clear understanding.
Example
4x + 4y = 4
3x - 3y = -3
If I solve these equations as these are linear and the power of xand y is 1.
Nonlinear Systems of Equations
It's the collection of two or more nonlinear equations that shared variables and the highest power of their variables is great than 1.
General Form
The general form of a nonlinear system of equations is as follows.
A1(x, y) = 0
A2(x, y) = 0
where A1, A2 are nonlinear functions of x and y.
Example
x^2 + y^2 = 5
x^2 - y^2 = 2
Here the the highest power of the variables (x and y) is more than 1.
So the basic difference are based on linearity in case of linear systems we have linear equations while nonlinear are presented in non linear equations.
As I mentioned above the power is 1 in case of linear systems while it's great than one in case of non linear systems.
On case of linear systems it can be solved by elimination or substitution while in non linear it requires the numerical methods.
Describe any one method for solving system of linear equations and share atleast one step by step algebric example (It should be other than substitution, elimination and graphing method)
Hence the use of Cramer's Rule method for linear equations.
Cramer's Rule is the method for solving systems of linear equations, here we used determinants. We will calculate the determinants of the coefficient matrix, Moreover the constant matrix too.
Step-by-Step Example
 |  |  |
|---|
Task 3
To solve these systems of linear equations, we can use various methods such as substitution, elimination, or matrices. Here, we'll use the elimination method for both systems.
 |  | 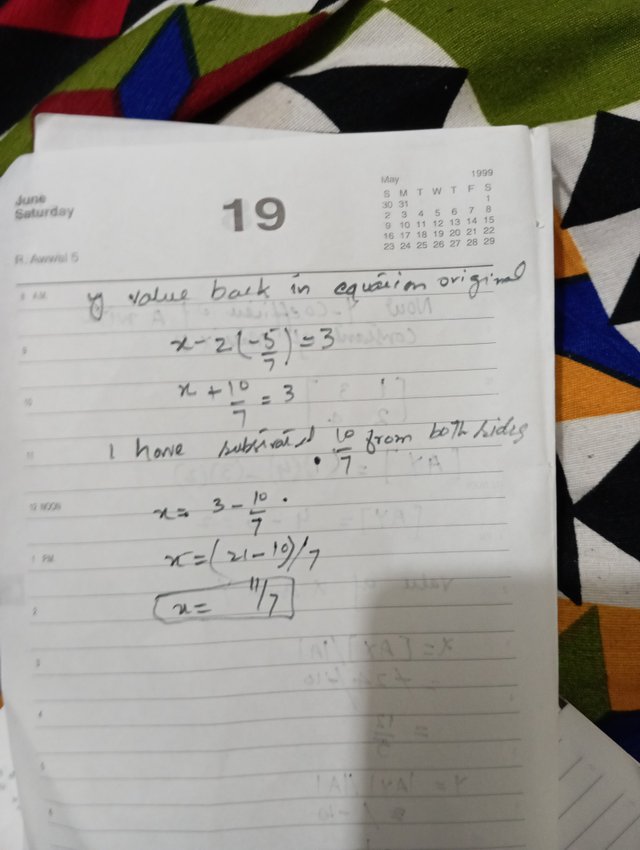 |
|---|
Task 4
Scenario 1
Here I have used linear equation.
2x + 3y = 130 (equation 1, cost of materials)
x + 2y = 110 (equation 2, cost of labor)
As we wanted to production of 60 units so I can write
A (x = 50), I am going to change the x value with equation 2.
50+2y=110
2y= 110-50= 60
Divide both sides by 2
Y= 60/2= 30
Result, in case of company production of 50 units A, they will produce 30 units for the product B.
Scenario 2
It would be solved by linear equations.
x + 2y = 80 (equation 1, cost of ingredients)
2x + y = 70 (equation 2, cost of labor)
As we mentioned that bakery will be produce 30 cakes of vanilla, I can write (x = 30). I will write the value of X in equation 1.
x+2y= 80
30+2y=80
I will solve y,
2y = 80 - 30
2y = 50
y = 50 / 2
y = 25
Hence bakery can produces 30 cakes of vanilla, there would be production of 25 cakes of chocolate.
I would like to invite my friends @m-fdo, @jannat12 and @iqrarana786 to take part in the challenge.
