"SLC-S22W3//Equations and Systems of equations."

casv (73)in #algebra-s22w3 • 25 days ago (edited)

_Fuente

Sistema de ecuaciones lineales

El sistema de ecuaciones lineales es un sistema conformado por ecuaciones de primer grado con características que la distinguen de un sistema de ecuaciones no lineal como los siguientes:

Forma general.
El sistema de ecuaciones lineales puede tener m ecuaciones con n incógnitas:

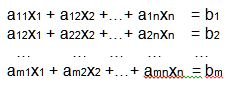
Donde a₁₁, a₁₂, … a_mn, son los coeficientes del sistema, x₁, x₂, …, x_n, son las incógnitas y b₁, b₂, …, b_m son los términos independientes.

Puede expresarse de matricialmente:

[A][x] = [b]

Donde [A] es la matriz de coeficientes del sistema de tamaño m por n, [x] es el vector columna de incógnitas de longitud m y [b] es el vector columna de los términos independiente de longitud m.

Grado.
Al tratarse de un sistema de ecuaciones lineales, todas las ecuaciones del sistema tienen grado 1, es decir, el máximo exponente de la variable de cada ecuación es igual a 1.

Soluciones.
Según el número de soluciones, los sistemas de ecuaciones se pueden clasificar de acuerdo a los siguientes casos:

Sistema compatible.
Si tiene una única solución el sistema es compatible determinado y cuando tiene infinitas soluciones el sistema es compatible indeterminado.

Sistema incompatible.
Sucede cuando el sistema no tiene solución en los números reales.

Representación gráfica.
El sistema de ecuaciones lineales como su nombre lo indica, representa un conjunto de líneas rectas que son posibles representar gráficamente en un plano cartesiano o espacio bidimensional.

La solución del sistema será un punto o línea donde se interceptan todas las rectas del sistema. Si no existe ningún punto de intersección el sistema es incompatible, es decir no tiene solución.

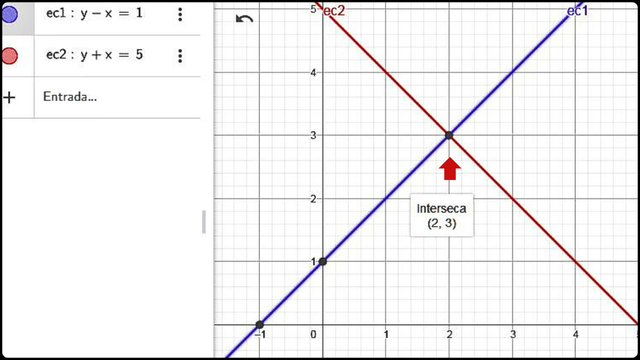_{Representación gráfica de un sistema de ecuaciones compatible determinado en el espacio bidimensional / Fuente}
También representa un conjunto de planos en un espacio tridimensional. Si dichos planos se interceptan en un único punto, este será la solución única del sistema. Por el contrario, si la intercepción es una línea recta o un plano, el sistema tendrá infinitas soluciones.

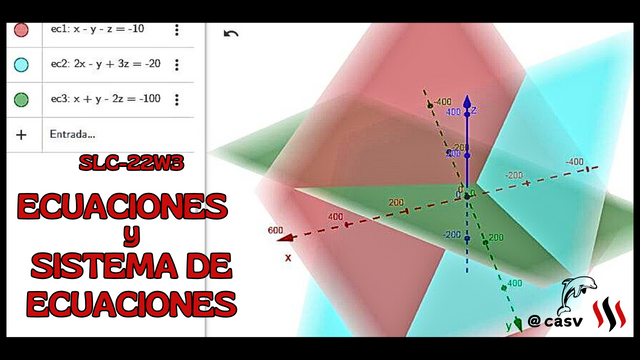
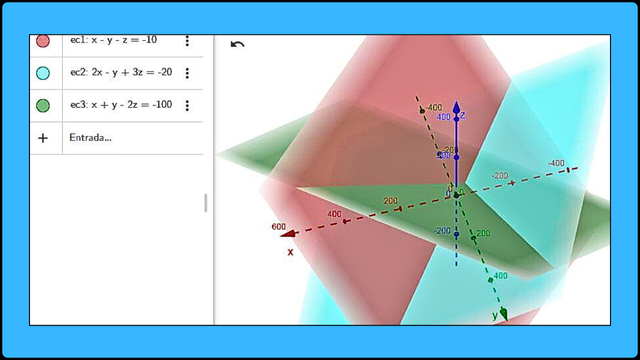_{Representación gráfica de un sistema de ecuaciones compatible determinado en el espacio tridimensional / Fuente}

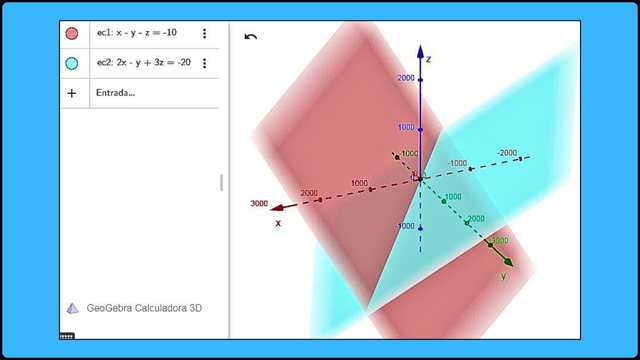_{Representación gráfica de un sistema de ecuaciones compatible indeterminado en el espacio tridimensional / Fuente}
Ejemplo algebraico:

-x + y = 1
x + y = 5

Si aplicamos el método de eliminación sumamos ambas ecuaciones y eliminamos “x” como sigue:

(-x+y)+(x+y) = (1+5) y tenemos,
2y = 6
y = 6/2

Por tanto, y = 3. Sustituimos el valor de “y” en cualquiera de las 2 ecuaciones y hallamos el valor de “x”:

En la segunda ecuación tenemos:

x+y =5

entonces si y= 3, tenemos, x+(3) =5
despejando “x” tenemos: y = 5-3

Por tanto, x= 2

La solución única al sistema de ecuaciones lineales es:

x=3
y=2

Ejemplo práctico:

Si Pedro gana un sueldo x y Juan gana 2 veces más que Pedro, ¿Cuánto gana cada uno si juntos alcanzan $1000?

Tenemos las siguientes condiciones:

El sueldo de Pedro y Juan totalizan $1000, por tanto se debe cumplir que :

x + y = 1000

También se condiciona el sueldo de Juan a 2 veces el de Pedro, entonces se cumple que:

y = 2x

Significa que se puede plantear un sistema de 2 ecuaciones lineales con 2 incógnitas como sigue:

x+y = 1000
2x –y = 0

Si sumamos ambas ecuaciones eliminamos la incógnita “y”, luego podemos hallar el valor de “x”, como sigue:

(x+y) + (2x-y) = 1000
3x = 1000
x = 1000/3

Luego sustituimos el valor de “x” en cualquiera de las dos ecuaciones y tenemos:

En la segunda ecuación 2x-y =0, x = 1000/3 y obtenemos:

2(1000/3) – y = 0
y = 2000/3

Por tanto, la solución única del sistema es (x;y) = (1000/3; 2000/3). Es decir que la respuesta es:

Pedro gana = 1000/3 y
Juan gana = 2000/3

Sistema de ecuaciones no lineales

El sistema de ecuaciones no lineales se presenta cuando al menos una de sus ecuaciones no es lineal, es decir, su grado máximo es mayor a 1. Por ejemplo, si una de las ecuaciones es cuadrática a pesar que el resto sea lineal, es un sistema de ecuaciones no lineal.

Forma general:
En este tipo de sistema podemos encontrar polinomios de segundo grado, raíces, logaritmos, exponenciales, etc. incluso acompañando ecuaciones de lineal o de primer grado. Por tanto, un sistema de ecuación no lineal tiene la forma:

f(u,v) = 0 para algún valor conocido de “u”.
g(u,v) = 0 para algún valor conocido de “v”.

Para resolver cualquier ecuación es necesita saber decidir en cual espacio matemático se encuentra la solución “u,v”. Es decir, “u,v” son números reales, vectores o funciones.

Por ejemplo:
x² + y² = 25
2x +y = 2

Soluciones.
Las ecuaciones no lineales son más complejas de resolver que las lineales y más difíciles de entender por la falta de soluciones simples superpuestas, ya que las soluciones generalmente no forman un espacio vectorial.

Al igual que en los sistemas de ecuaciones lineales, en el sistema de ecuaciones no lineales puede existir una solución o par ordenado que satisface las ecuaciones del sistema. Sin embargo, en un sistema no lineal pueden resultar más de una solución.

Con el sistema de ecuaciones no lineales las soluciones suelen ser puntos de intersección de gráficas curvas, parábolas e hipérbolas, etc.

Representación gráfica.
Cada ecuación del sistema de ecuaciones no lineales se puede representar gráficamente para determinar los puntos de intersección. Cabe destacar que la representación gráfica es posible en el espacio bidimensional y tridimensional.

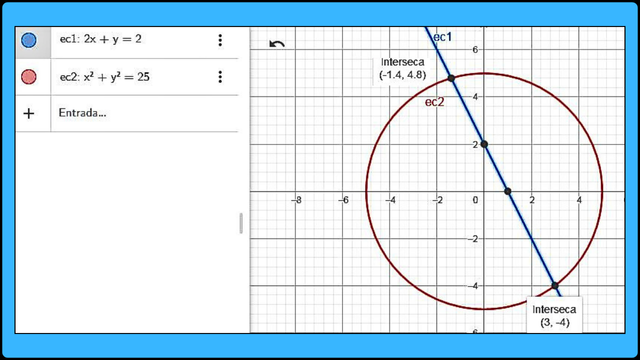_{Representación gráfica de un sistema de ecuaciones no lineales en el espacio bidimensional / Fuente}
Ejemplo algebraico:

x² + y² = 25
2x +y = 2

Se despeja “y” de la ecuación lineal:

y = 2 – 2x, luego sustituimos en la ecuación cuadrática:

x² + y² = 25

x² + (2-2x) ² = 25
x² + (4-2(2)(2)x+4x²) = 25
x² +4 -8x +4+4x² = 25
5x² - 8x +4 -25 = 0
5x² - 8x -21 = 0

Resolver la ecuación cuadrática: 5x² - 8x -21 = 0

Utilizando la solución típica de la cuadrática:

x=(-b ± √(b^2-4ac))/2a

Tenemos:
a= 5, b= -8, c= -21

x = (8 ± √(-8^2-4(5)(-21))/2(5)
x = (8± √(64+420))/10
x = (8 ± √484)/10
x = (8 ± 22)/10

x₁ = (8 + 22)/10 = 30/10 = 3
x₂ = (8 - 22)/10 = -14/10 = -1.40

Por tanto, tenemos (x₁;x₂) = (3;-1.40). Calculemos los valores y₁ y y₂ respectivamente en la segunda ecuación como sigue:

Para x₁ = 3
2(3)+ y₁ = 2
y₁ = 2 -6
y₁ = -4

Para x₂ = -1.40 2(-1.40)+ y₁ = 2
y₁ = 2 + 2.80
y₁ = 4.80

Tenemos dos soluciones:
(x;y) = (3;-4)
(x;y) = (1.4;4.8)

Ejemplo práctico.

Tenemos dos objetos A y B. El objeto A cae libremente desde una torre de 100 m y el objeto B se desplaza horizontalmente a una velocidad constante de 2 m/seg ¿Cual es la distancia recorrida por el objeto B cuanto el objeto A haya alcanzado el suelo?

El movimiento del objeto A se rige según la ley de Newton, en caída libre se plantea la siguiente ecuación:

y = 1/2 gt²

donde "y" es la distancia vertical recorrida (100 m), "t" es el tiempo transcurrido en dicha distancia, "g" es una constante igual a 9.80 m/seg². Siendo así tenemos la primera ecuación del sistema: (1/2)(9.80)t² = 100. Por tanto,

4.90t² -100 =0 : (ec.1)

El objeto B parte de reposo y se deplaza en un movimiento no acelerado, se rige por la siguiente ecuación de movimiento uniforme:

x = Vt, donde V es la velocidad (2 m/seg) y "t" el tiempo transcurrido para la caida libre. Por tanto, se define una segunda ecuación como x = 2t, por tanto,

x - 2t = 0 : (ec. 2)

El sistema a resolver es de dos ecuaciones y dos incógnitas:

4.90t² - 100 =0
x - 2t = 0

Procedemos a despejar x de la segunda ecuación:

x = 2t , luego lo sustituyo en la primera ecuación:

4.90 (2t)² - 100 = 0
4.90 (4)t² = 100
19.60t² = 100
t² = 100/19.60

t = ±√(100/19.60) = ± 2.26

Por lo tanto, siendo el tiempo un valor real positivo, t = 2.26 seg. Significa el tiempo en que el objeto A toca el suelo. Sustituimos en la segunda ecuación para determinar el valor de "x"

x -2t = 0 para t = 2.26 tenemos
x = 2(2.26) = 4.52

La solución al sistema es (x;t) = (4.52;2.26)

Respuesta. El objeto B recorre 4.52 m al momento en que el objeto A toca el suelo.

Método de Cramer

Se trata de una solución al sistema lineal de ecuaciones en términos de determinantes aplicando la regla de Cramer. Es un sistema de importancia teórica por lo explícito en dar una solución y ser práctico para sistemas lineales que no excedan tres ecuaciones.

Resulta ineficiente para grandes matrices por el excesivo proceso computacional que implican muchas ecuaciones.

La regla de Cramer es válida para sistemas lineales de ecuaciones compatibles con una solución única que cumplan dos condiciones:

El sistema debe tener tantas ecuaciones como incógnitas
El determinante de la matriz de los coeficientes del sistema debe ser distinto de cero.

El sistema de Cramer tiene la siguiente forma:

[A][x] = [b]

Donde,
[A] es la matriz de coeficientes del sistema
[x] es el vector columna de las incógnitas
[b] es el vector columna de los términos independientes.

Por tanto, la solución al sistema es:

x_i = |A_i| / |A|

Donde |A_i| es el determinante de la matriz resultante de reemplazar la i-ésima columna de [A] por el vector columna [b] y |A| es el determinante de la matriz de coeficientes [A].

Expresado de otra manera, si tenemos un sistema de ecuaciones lineales en general:

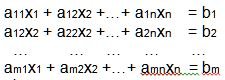
El determinante de la matriz de coeficientes |A| vendría dado por:

Por tanto, el determinante |A₁| viene dado por:

Por tanto, la solución x₁= |A₁| / |A|

El determinante |A₂| viene dado por:

Por tanto, la solución x₂ = |A₂| / |A|

El determinante |A_n| viene dado por:

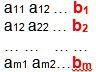
Por tanto, la solución x_n = |A_n| / |A|

Vayamos a un ejemplo práctico donde se reflejarán estos conceptos.

Ejemplo algebraico:

Tenemos un sistema compatible y determinado de 2 ecuaciones con 2 incógnitas.

2x + 1y = -2
3x + 2y = 4

Paso 1. Hallar el determinante |A| de la matriz de coeficientes como sigue:
Determinante |A|:

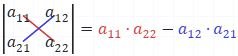
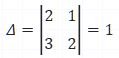
|A| = (2)(2) - (3)(1) = 4-3

|A| = 1

Paso 2. Hallar los determinantes resultantes de sustituir el vector columna b en cada vector columna de A.

Determinante |A₁|:

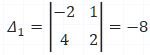
|A₁| = (-2)(2) - (4)(1) = -4 - 4 = - 8

Determinante |A₂|:

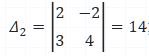
|A₂| = (2)(4) - (3)(-2) = 8 + 6 = 14

Paso 3. Calcular los valores de las incógnitas x,y como sigue:

x = |A₁| / |A| = -8/1 = - 8
y = |A₂| / |A| = 14/1 = 14

Respuesta:

x = -8
y = 14

(a):
x + 2y = 7
3x - 2y = 5

En este sistema podemos aplicar el método de eliminación al sumar las dos ecuaciones para eliminar el término “2y” y luego despejar “x” , como detallo a continuación:

x + 2y =7
3x - 2y = 5
- Sumando tenemos: (x + 3x) = (7 + 5)
- Simplificando: 4x = 12
- Dividimos por 4 ambos lados: x = 12/4
Por tanto, el valor de x = 3

Sustituimos el valor de “x” en la primera ecuación para tener “y”:

x + 2y = 7
- Sustituimos el valor de “x” y tenemos: 3 + 2y = 7
- Restamos 3 en ambos lados: 2y = 7 - 3
- Simplificamos a 2y =4
- Dividimos por 2 ambos lados y = 4/2
Por tanto, simplificando y = 2

Comprobamos sustituyendo los valores de “x” y “y” en cualquiera de las ecuaciones. Verificamos con la segunda ecuación:

3x - 2y = 5
- Sustituyendo tenemos: 3(3) - 2(2) = 5
- Resolvemos las multiplicaciones del lado izquierdo: (9 – 4) = 5
- Simplificando tenemos: 5= 5
¡Comprobado!

Por tanto, la solución (x;y) = (3;2) es el resultado correcto porque satisface el sistema de ecuaciones.

(b):
4x + 6y = 2
x - 2y = 3

En este sistema aplicaré el método de sustitución, por tanto, despejaré la variable “x” de las segunda ecuación como detallo a continuación:

x - 2y = 3

Sumamos “2y” a cada lado y tenemos: x = 3 + 2y
Sustituimos esta “x” en la primera ecuación para tener “y”:

4x + 6y = 2
- Sustituimos “x” y tenemos: 4(3+2y) + 6y = 2
- Resolvemos la multiplicación: 12 + 8y + 6y = 2
- Sumamos términos semejantes: 14y + 12 = 2
- Restamos 12 en ambos lados: 14y = 2 - 12
- Sumamos a la derecha: 14y = -10
- Dividimos por 14 ambos lados: y = -10/14
Por tanto, simplificando y = -5/7

Sustituimos el valor de “y” en la expresión de previamente despejada como indico a continuación:

Tenemos x = 3 +2y
- Sustituyendo el valor de “y” tenemos: x = 3 + 2(-5/7)
- Resolvemos la multiplicación y tenemos: x = 3 - 10/7
- Resolvemos la suma: x = [(3)(7) - 10]/7 = (21 - 10)/7
- Resolvemos el numerador de la fracción: x = 11/7
Por tanto, simplificando x = 11/7

Teniendo los valores de x = 11/7 y y = -5/7, procedemos a comprobar el resultado sustituyendo dichos valores en cualquiera de las dos ecuaciones analizadas. Verificamos en la segunda ecuación:

Tenemos la segunda ecuación: x - 2y = 3
- Sustituyendo los valores de (x;y) tenemos: 11/7 - 2(-5/7) = 3
- Resolvemos la multiplicación y tenemos: 11/7+10/7 = 3
- Sumamos las fracciones a la izquierda: 21/7 = 3
- Simplificamos la fracción: 3 = 3
¡Comprobado!

(x;y) = (11/7;-5/7)

Escenario número 1

Supongamos que hay una empresa que fabrica dos productos, A y B. Si el coste de producir “x” unidades de A y “y” unidades de B viene dado por el sistema, entonces:

2x + 3y = 130 (costo de los materiales)
x + 2y = 110 (costo de la mano de obra)

Si la empresa quiere producir 50 unidades del producto A, calcule cuántas unidades del producto B puede producir.

Costo total = 3x + 5y = 240

x = 50

Sustituyendo el valor de x=50, tenemos: 3(50) + 5y = 240
Resolviendo el producto: 150 + 5y = 240
Restando 150 en cada lado: 5y = 240-150
Dividiendo por 5 ambos lados: y = 90/5

y = 18

Respuesta

Análisis del resultado e interpretación

Escenario número 2

Supongamos que en una pastelería se producen dos tipos de pasteles: de vainilla y de chocolate, y que el coste de producción de “x” pasteles de vainilla y “y” pasteles de chocolate viene dado por el sistema;

x + 2y = 80 (costo de los ingredientes)
2x + y = 70 (costo de la mano de obra)

Si la panadería quiere producir 30 pasteles de vainilla, ¿cuántos pasteles de chocolate puede producir?

Costo total = 3x + 3y = 150

x = 30