SLC S22W3//Equations and Systems of equations
It feels good to be part of another edition of this brain challenge that helps one think fast and in the process, avoid making mistakes when finding solutions to problems. This is the relationship of two people. You need to know how much each of them worth in such a way that the relationship won't suffer from financial dark sides. How would you know? You can know this by first determining how much the man has transferred to this woman if given the account statement as the equation.
If you can decipher this, you'll know how much either the man has or the woman. You would definitely use methods like eliminating the odd ones out of the account statement so you'll know all the transactions of the man to the woman and the woman to the man. After determining how much is transferred to the woman, you can find out a range at which her account balance reads. 😂😂 Just kidding though. I'm trying to clear my head before starting this mathematically journey. Follow through and see how I did answer all assignment questions with ease.
Explain difference between linear and non linear systems of equations. Provide examples of each type of system of equation and describe their general forms. |
|---|
When we talk about linear and non-linear systems of equation, we are actually directing people's attention to relationships involving straight lines which is linear and it's very simple and one-way but non-linear is complex and are presented in curves other than just straight lines. The differences are clearly seen in their definition. Let me give a breakdown.
Definition
Linear systems of equation: It's actually a system where each equation represents a straight line. The equation is just straight and plain with no complications attached. What do I mean? Each variable has a degree of one. In Linear equation, there are no cubes, squares or other powers attached to the variables involved and each terms involved in the equation is either a constant value, the product of a constant or a single variable.
Linear: y = 4x + 7
Where y represents the dependent variable which value depends on the value of x. As x changes, so does y according to the question. The equality sign means that y depends on 3x - 7
- 3x represents the slope graphically which indicates the rate of change of y with respect to the variable x.
- x represents the independent variable
- 7 represents the intercept C, which represents the point where the line crosses the y-axis.
- General Forms: It has the general form as....
ax + by = c1
a1x + b1y = c1
In this general form, a, b, c are constants and X and Y are variables.
Example: it could be a two variable system as;
3x + 5y = 7
x + 4y = 3
Graphically, if we're using the first equation y = 2x + 1. The line starts from y = 1 when x = 0. Slope which is M in mx is 2 which means that for every unit it runs, it rises 2 units.
Non-linear Systems of Equation
This is simply the reverse of linear equation where the one or more equations involve squares, cubes or more. It has at least one equation that isn't linear and its graph isn't straight line but curved. As a complex function, it could exist as components of trigonometry, exponential or logarithms.
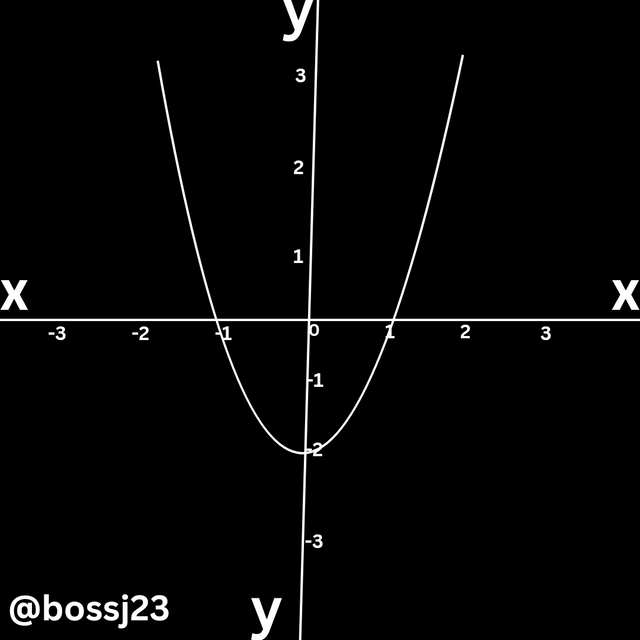
Example: y = x² + 2x + 3
In this example, the variables are raised to the power of 2 and 1.
General Form
ax² + bxy + cy² + dx + ey + f = 0
f1(x, y) = 0
f2(x, y) = 0
3x² + 2y² = 4
3x + y = 3
Graphically, non-linear systems of equation have curves such as parabolas or hyperbolas in their graph which isn't straight line like that of linear.
y = x² + 2 and y=4x + 7
These are the clear differences between linear and non-linear systems of equation.
Describe any one method for solving system of linear equations and share atleast one step by step algebric example. |
|---|
The question says we should describe first before sharing an example or illustration with which it's applied. This was difficult for me at first because I don't like describing mathematics but come to think of it, we're talking about elimination method. The name alone should tell you what it is all about, we eliminate to get the value of something.
This method is widely used to solve systems of linear equation as an algebraic technique and the main aim of this technique is for us to find the values of the variables involved in the equations, that satisfies it simultaneously.
We remove one if the variables by addition or subtracting the equations so we can eliminate one, get the value of one and then use the value of the one gotten to born another value from the dead equation. How possible? I'll show you. This method works best for systems where the equation is expressed as .....ax + by = c which equations has to align for the elimination to take place.
Let me describe the procedures before giving an example.
Process
In elimination method, you have to first of all combine the equations together and then align the equation. The equations should be in standard form with similar variables. Not taking X to z and taking y to x
After aligning the equations, we'll match the coefficients. If the coefficients of the variable up is not the same as the variable down since we are eliminating either x or Y, we'll ensure we use the coefficient of one equation that is bigger to multiply the one that is smaller and then we'll use the smaller coefficient to multiply the larger coefficient equation. This would be explained extensively.
- After matching coefficients, we'll eliminate by adding or subtracting. We use the signs in the equations to know if we are to add or subtract. If the coefficients are the same, we'll subtract but if they are not, we'll add.
- After elimination, we'll use the value gotten either for X or Y to find the remaining variable by substituting the value with the known variable in the first equation to get the second variable value.
- To check, we'll substitute both values to see if they'll satisfy the equation.
Example |
|---|
Solve the system of equations
2x + 3y = 12.....1
x - 3y = 3.......2
Solution
Step 1: Looking at these equations, we'll have to align it to know if the coefficients are the same or not. This will help us know if we are adding to eliminate or subtracting.
2x + 3y = 12.....1
x - 3y = 3.......2
Step 2: Let's match coefficients.
2x + 3y = 12.....1
x - 3y = 3.......2
If you notice, the y variable has the same coefficient but different signs. Remember, when the coefficient are different, we add in elimination method that's after matching.
- 3y
- 3y
If these two are subtracted with the main equation, we would have no reasons to cancel a variable out because x would still remain and y becomes 6y. If we are to add, we eliminate the y variable.
- Step 3: Adding the equations to eliminate y, we do....
2x + 3y = 12.....1
- x - 3y = 3.......2
3x + 0 = 15......3
3x = 15
- Step 4: Divide both sides of the equation by the coefficient of X to make x stand out.
3x/3 = 15/3
x = 5.
- Step 6: Let's substitute this value of X in equation 1 to know the value of y.
For x=5,
2x + 3y = 12.....1
2(5) + 3y = 12
10 + 3y = 12
We'll collect like terms from here.
3y = 12-10
3y = 2.
Divide both sides by the coefficient of y
3y/3 = 2/3
y = 2/3.......
x = 5; y=2/3 ✅
To check your answer |
|---|
Substitute the value of X and Y in both equations to see if they satisfy the equation....
For equation 1;
2x + 3y = 12.....1
x = 5 and y = 2/3
2(5) + 3(2/3) = 12
10 + 6/3 = 12
10 + 2 = 12 ✅ It satisfies it.
Let's move to equation 2
x - 3y = 3.......2
For x = 5; y = 2/3
(5) - 3(2/3) = 3
5 - 6/3 = 3
5 - 2 = 3 ✅✅ It satisfies the equation. So both values are correct.
You need to solve the following system of linear equations: (a) x + 2y = 7, 3x - 2y = 5 (b) 4x + 6y = 2, x - 2y = 3 (You are required to solve these problems at the paper and then share clear photographs for adding a touch of your creativity and personal effort which should be marked with your username) |
|---|
You need to solve the following system of linear equations: (a) x + 2y = 7, 3x - 2y = 5
Solution.....
We'll use the elimination method for this particular one as it's straightforward_. The equations in question are;
x + 2y = 7, 3x - 2y = 5
- Step 1: We'll align the equations to suit our needs to check if the variables are the same.
x + 2y = 7
3x - 2y = 5
- Step 2: After aligning the equations, we'll match the coefficients to check if they are ohkay. This helps us know either to subtract or add.
x + 2y = 7
3x - 2y = 5
In this equation, the x variables are different and the coefficient of the y variables are quite the same but different signs. So we'll have to add the coefficient to eliminate the value of y because subtracting it would make the two variables remain and they'll be no eliminations again.
Step 3: Add the equations to eliminate y.
x + 2y = 7
3x - 2y = 5
4x + 0 = 12
4x = 12
Let's divide both sides by the coefficient of X to know the value of x
4x/4 = 12/4
x = 3
 | 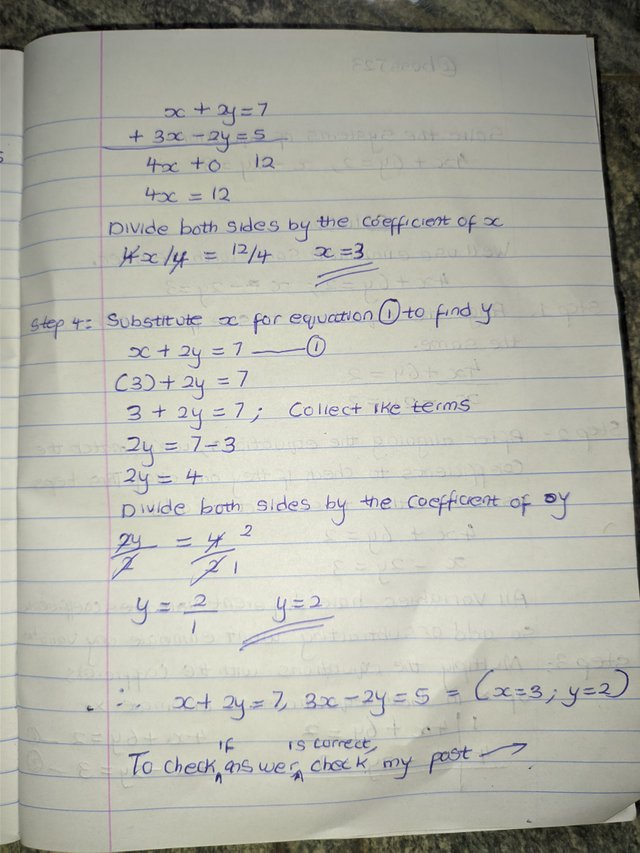 |
|---|
We've gotten our X as 3, so we'll substitute it in equation 1 to know the value of y. Let's do this.....
x + 2y = 7
For x = 3;
(3) + 2y = 7
3 + 2y = 7
From here, we'll collect like terms.....
2y= 7-3
2y = 4
Divide both sides by the coefficient of y.
2y/2 = 4/2
y = 2
Therefore; our x = 3 and y = 2.
To check if our answer is correct |
|---|
Let's substitute both values in the two equations to see if they satisfy the equations
For equation 1;
x = 3 and y = 2
(3) + 2(2) = 7
3 + 4 = 7 It satisfies the equation ✅✅✅
For equation 2,
x = 3 and y = 2
3x - 2y = 5
3(3) - 2(2) = 5
9 - 4 = 5....It satisfies the Equation ✅✅✅
4x + 6y = 2, x - 2y = 3 (You are required to solve these problems at the paper and then share clear photographs for adding a touch of your creativity and personal effort which should be marked with your username)
You need to solve the following system of linear equations: (a) 4x + 6y = 2, x - 2y = 3
Solution.....
We'll use the elimination method for this particular one as it's straightforward_. The equations in question are;
4x + 6y = 2, x - 2y = 3
- Step 1: We'll align the equations to suit our needs to check if the variables are the same.
4x + 6y = 2
x - 2y = 3
- Step 2: After aligning the equations, we'll match the coefficients to check if they are ohkay. This helps us know either to subtract or add.
4x + 6y = 2
x - 2y = 3
In this equation, the x variables are different and the coefficient of the y variables are different. So we'll have to multiply the coefficients of x to eliminate the value of X because subtracting or adding it would make the two variables remain and there'll be no eliminations again.
Step 3: Multiply the equations with the coefficients of X in both equations to eliminate x**.
> 4x + 6y = 2
x - 2y = 3
| 1 | 4x + 6y = 2 |
|---|---|
| 4 | x - 2y = 3 |
4x + 6y = 2.........(1)
4x - 8y = 12...........(2)
Step 4: Subtract the equations with the coefficients of X in both equations to eliminate x*.
4x + 6y = 2.........(1)
-4x - 8y = 12.........(2)
- 14y = - 10
Divide both sides by the coefficient of y
14y/14 = - 10
y = - 10/14
using two to divide both numerator and denominator
y = - 5/7
We've gotten our y as 5/7, so we'll substitute it in equation 1 to know the value of y. Let's do this.....
Substitute y for equation 2....
x - 2(-5/7) = 3
.x + 10/7 = 3
Collect like terms
x = 3 - 10/7
Solving the fraction...LCM
x = 7(3/1) - 7(10/7)
x = 21 - 10/7
x = 11/7 ✅✅✅
 | 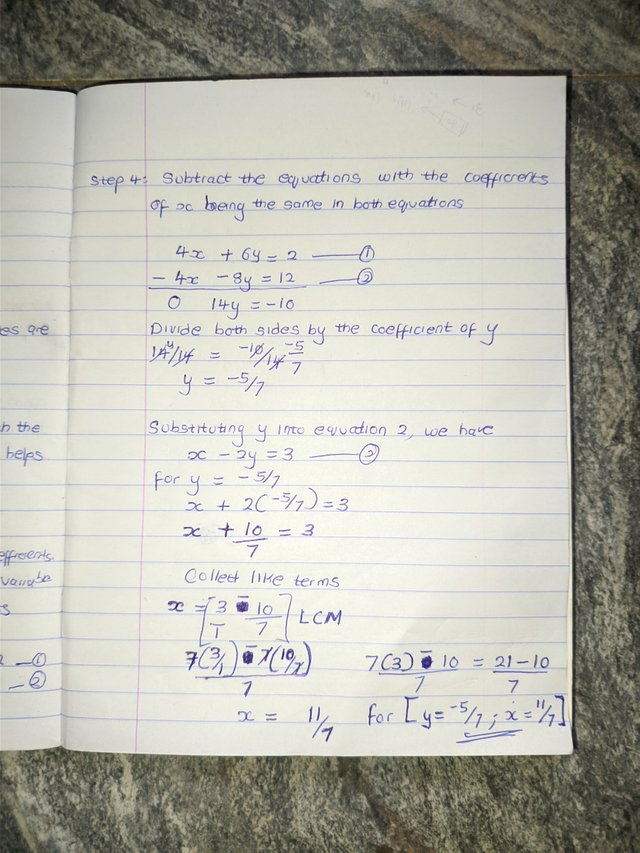 |
|---|
Therefore; our x = 11/7 and y = - 5/7.
To check if our answer is correct |
|---|
Let's substitute both values in the two equations to see if they satisfy the equations
For equation 1;
x = 11/7 and y = - 5/7
4(11/7) - 6(-5/7) = 2
44/7 + 30/7 = 44-30/7
14/7 = 2 * It satisfies the equation ✅✅✅
For equation 2,
x = 11/7 and y = -5/7
x - 2y = 3
**(11/7) - 2(-5/7) = *
11+10/7 = 21/7
21/7 = 3 It satisfies the Equation ✅✅✅
| Graphically, couldn't reach out to graph sheet and dislike using paper | 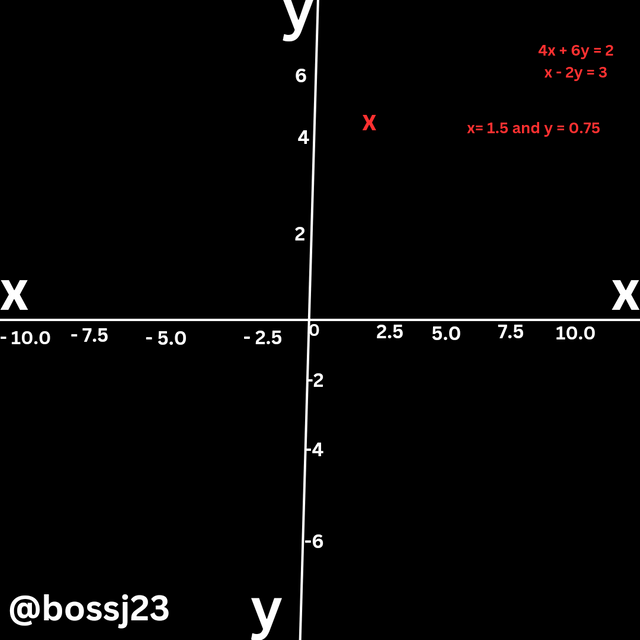 |
|---|
Task 4 |
|---|
Suppose there's a company producing two products, A and B.If cost of producing x units of A and y units of B is given by system then;
2x + 3y = 130 (cost of materials)
x + 2y = 110 (cost of labor)
If company wants for producing 50 units of product A then calculate how much units of product B they may produce?
For this task, we are given a system of linear equations.
2x + 3y = 130 (cost of materials)
x + 2y = 110 (cost of labor)
2x + 3y = 130 ....A
x + 2y = 110.....B
From the question , the company wants to produce x = 50 units of product A. Which we are to find y to know how many units of product B they may produce.
Note: x = 50 units
- Step 1 Substitute x = 50 into equations A and B
For equation 1, where x = 50
2x + 3y = 130 ....A**
2(50) + 3y = 130.....
100 + 3y = 130
Collect like terms
3y = 130 - 100
3y = 30
Divide both sides by the coefficient of y
3y/3 = 30/3
y = 10.......(1)
Putting this value y in equation 2 to see if we can get another value of y
For equation 2 where x = 50
x + 2y = 110.....B
50 + 2y = 110
Collect like terms
2y = 110-50
2y = 60
Divide both sides by the coefficient of y
2y/2 = 60/2
y = 30
So our y = (10, 30)
Final Thoughts |
|---|
The values are very much inconsistent because they are different. The systems of equation is inconsistent because no value will satisfy both equations. So, 50 units of product, materials, and labor involved will be inconsistent. Production cost would be inconsistent with material costs and product labor.
Scenario 2
Suppose there's a bakery producing two types of cakes which are vanilla and chocolate.If cost of producing x cakes of vanilla and y cakes of chocolate is given by system then;
x + 2y = 80 (cost of ingredients)
2x + y = 70 (cost of labor)
If bakery wants for producing 30 cakes of vanilla then calculate how much cakes of chocolate can they produce?
It's more like the first but different equations involved. For this task, we are given a system of linear equations.
x + 2y = 80 (cost of ingredients)
2x + y = 70 (cost of labor)
x + 2y = 80....A
2x + y = 70....B
From the question , the bakery wants to produce x = 30 cakes of vanilla which we are to find y to know how many cakes of chocolate they can produce.
Note: x = 30 cakes
- Step 1 Substitute x = 30 into equations A and B
For equation 1, where x = 30
x + 2y = 80
(30) + 2y = 80.....
30 + 2y = 80
Collect like terms
2y = 80 - 30
2y = 50
Divide both sides by the coefficient of y
2y/2 = 50/2
y = 25.......(1)
Putting this value y in equation 2 to see if we can get another value of y
For equation 2 where x = 30
2x + y = 70.....B
2(30) + y = 70
Collect like terms
y = 70 - 60
y = 10
y = 10
So our y = (25, 10)
Final Thoughts |
|---|
The values are very much inconsistent because they are different. The systems of equation is inconsistent because no value will satisfy both equations. So production costs and cakes of vanilla and chocolate are inconsistent.
Most pictures are gotten from Canva
I invite @memamun, @zulbahri and @vivigibelis
Cc,
@khursheedanwar





@tipu curate
Upvoted 👌 (Mana: 7/10) Get profit votes with @tipU :)