SLC-S22W2 | Ecuaciones y Desigualdades
Saludos amigos steemians.

Las ecuaciones representan soluciones matemáticas para distintos escenarios de la vida cotidiana, permitiendo dar soluciones óptimas en diversas áreas de estudio, entre ello el calculo de precios, distancias, tiempos, entre otros.
Explicar la diferencia entre ecuaciones lineales y cuadráticas. Proporcionar ejemplos de cada tipo de ecuación y describir sus formas generales.
Ecuaciones Lineales
Son aquellas cuya representación gráfica proporciona como resultado una línea recta, y se caracteriza por presentar siempre la mayor potencia de la variable en el grado máximo 1. Pueden tener una, dos, tres o más variables.
Su froma general es ax + b = 0, donde a y b son constantes y x es la variable. Un ejemplo de ello, sería 3x + 2 = 0.
Un ejemplo práctico sería una jóven que compra 5 fichas para el acceso al internet, y cada una tiene 20 minutos gratis. Se desea saber las horas tendrá de acceso a internet con sus 5 fichas.
X = 60minutos
X+ 20 = x minutos
60 + 20 = 80 minutos = 1.33 horas
Entonces, 5 fichas de 1.33 horas = 6.66 horas dispone para conexión a internet.
Ecuaciones Cuadráticas
También llamadas ecuaciones de segundo grado son aquellas en donde el exponente del término desconocido está elevado al cuadrado, es decir, la incógnita está elevada al exponente 2. Tienen la forma general de un trinomio:
ax² + bx + C =0
Donde a, b y c son números reales y se conocen como coeficientes. Así, a es el coeficiente de x², b es el término o coeficiente de x y c es el término independiente. Un ejemplo de ello sería 2x² + 3x - 4 = 0
La representación gráfica de este tipo de ecuaciones es una parábola; siendo el valor del coeficiente de x² el que determina la forma de la curva. Si a es menor que 0, la parábola abra hacia abajo, es decir tiene forma de n; pero si a es mayor que 0 la parábola abre hacia arriba, es decir tiene forma de U.
Un ejemplo práctico sería una pelota que es lanzada al aire desde el techo de una casa; su altura (h) sobre el suelo en metros, después de t segundos está dada por la función h(t)=−5t²+10t+20 .
En síntesis, se muestran a continuación las principales diferencias entre las eciaciones lineales y ecuaciones cuadráticas:
| Características | Ecuación lineal | Ecuación cuadrática |
|---|---|---|
| Forma general | ax + b = 0 | ax² + bx + C = 0 |
| Grado | 1 | 2 |
| Gráfico | Línea Recta | Parábola |
| Solución | Una solución | Dos soluciones |
| Ejemplo | 3x+2= 0 | 2x² + 3x - 4 = 0 |
Describir dos tipos diferentes de desigualdades (que no se explican en el curso). Proporcionar ejemplos de cada tipo de desigualdad y explicar cómo resolverlas.
La desigualdad se considera una proposición que relaciona dos expresiones algebraicas, en las que los valores son distintos; es decir relaciona dos elementos diferentes, ya sea por desigualdad mayor, menor, mayor o igual, menor o igual, etc. Cada una de las diferentes tipologías de desigualdad tienen una reacción a operaciones matemáticas diferente según su naturaleza.
1.- Desigualdades Estrictas
Es un tipo de desigualdad que excluye la igualdad, es decir que si se tienen dos valores, digamos a y b, una desigualdad estricta indicaría que a es estrictamente menor que b o a es estrictamente mayor que b; es decir no se permite la posibilidad de que a pueda ser igual a b.
Un ejemplo algebraico sería: 5x + 8 > 18
| Desigualdad | 5x + 8 > 18 |
|---|---|
| Se pasa el 8 al otro lado, con el signo contrario, es decir, a restar | 5x > 18 - 8 |
| El término que acompaña la incógnita se pasa al otro lado | x > 10 / 5 |
| Entonces, la solución viene dada por | x > 2 |
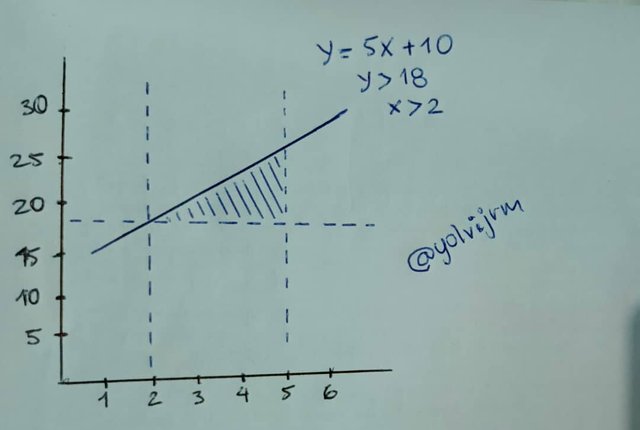
Un ejemplo práctico de ello sería un equipo de fútbol que acepta jugadores que tengan más de 18 año para poder fomar parte del equipo. Si un joven tiebe 5x + 10 años , ¿a partir de qué valor de (x) puede formar parte de ellos?
La desigualdad (5x + 10 > 18) permite encontrar que (x >2), por lo que la persona debe tener un mínimo de 2 unidades adicionales para ser elegible.
La representación gráfica de este tipo desigualdad viene dada por una línea recta. En este casouna recta dada por y = 5x + 10 y una región encima de esta línea para (x > 2).
2.- Desigualdades Racionales.
Es aquella desigualdad entre dos expresiones que forman una fracción, y en la cual la incógnita puede estar presente en el numerador, el denominador o ambos.
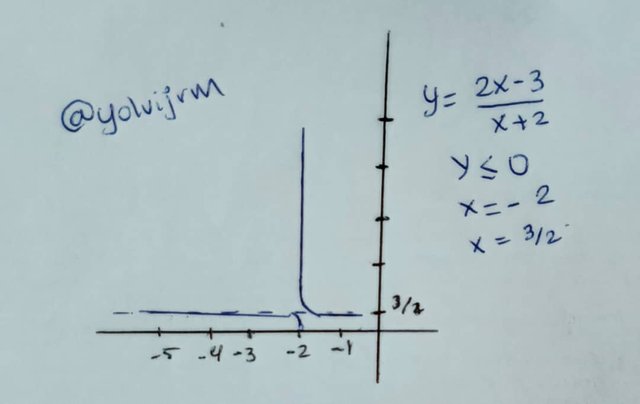
Un ejemplo algebraico sería: ((2x−3)/(x+2))≤0
| Desigualdad | ((2x - 3) / ( x + 2)) ≤ 0 |
|---|---|
| Se identifican los valores críticos | 2x − 3 = 0 ⟹ x =3/2 ; 𝑥 + 2 = 0 ⟹ 𝑥 = -2 |
| Dividir el eje (x) en intervalos | (−∞,−2), (−2,3/2), (3/2,+∞) |
| Se prueban los intervalos | La desigualdad se satisface para x∈(−2 , 3/2 ]. |
| La solución viene dada por | x∈(−2 , 3/2 ] |
Un ejemplo práctico de ello, sería un negocio que para obtener utilidad en sus operaciones, la relación entre las ventas (2x - 3) y la suma de gastos incurridos (x + 2) es menor o igual a (0). La desigualdad ((2x−3)/(x+2))≤0 ayuda a determinar en qué rango de ventas se obtiene la utilidad.
La representación gráfica de esta desigualdad se representa mediante una curva fraccionaria, con una región ubicada bajo el eje (x) entre los valores críticos (-2) y (3/2).
Resuelva la siguiente ecuación lineal: 2x + 5 = 11. Muestre la solución paso a paso y comparta su ejemplo práctico de cómo se puede aplicar esta ecuación en un escenario de la vida real.

Un ejemplo práctico de ello sería una persona que tiene 11 $ y gasta 5 $ en una comida; el dinero restante lo utiliza para comprar dos bebidas que tienen el mismo precio. Se pide determinar el valor de cada bebida.
En este caso, el costo total está representado por la ecuación (2x + 5 = 11), donde x es el precio de una bebida, 2x es el costo total de las dos bebidas, 5 es la cantidad gastada en la comida y 11 es la cantidad total de dinero disponible.
| Ecuación | 2x +5 = 11 |
|---|---|
| El término independiente pasa al otro lado, con signo contrario | 2x = 11 - 5 |
| Resolver la resta de la parte derecha de la ecuación | 2x = 6 |
| El 2 que acompaña a la x pasa al otro miembro con operación inversa | x = 6 / 2 |
| Entonces se tiene que | x = 3 |
Lo anterior significa que cada bebida tiene un valor de 3 $.
Escenario: La panadería de Tom
La panadería de Tom es una de las más famosas de la ciudad y es famosa por sus deliciosos pasteles y panes. Tom, el propietario, quiere asegurarse de tener suficientes ingredientes para satisfacer las necesidades de su famosa torta de chocolate y su receta de torta de chocolate. Necesita 2 tazas de harina, 1 taza de azúcar y 1/2 taza de cacao en polvo para cada torta.
1.- Ecuación: Si Tom quiere hacer x pasteles y tiene 10 tazas de harina, 8 tazas de azúcar y 4 tazas de cacao en polvo, ¿calcula el número de pasteles que puede hacer Tom?
En este caso cada ingrediente impone una restricción en la cantidad de pasteles que Tom puede hornear.
En relación a la harina, se tiene que cada pastel requiere 2 tazas, si se ecide preparar (x) pasteles, la desigualdad se convierte en 2x≤10.
2x ≤ 10
x ≤ 10 / 2
x ≤ 5
Esto significa que la harina limita a Tom a un máximo de 5 pasteles .
Teniendo en cuenta el azúcar, cada pastel requiere 1 taza, esto nos da la desigualdad 𝑥≤8., lo que significa que el azúcar disponible es suficienre para preparar hasta 8 pasteles.
En cuanto al cacao, cada pastel necesita 0,5 tazas, por lo que la desigualdad queda en 0,5x ≤ 4.
0,5x ≤ 4
x ≤ 4 / 0,5
x ≤ 8
Esto significa que la cantidad de cacao disponible también permite preparar hasta 8 pasteles
Conclusión: Aunque el azúcar y el cacao son suficientes para hacer hasta 8 pasteles, la harina es el factor limitante, esto quiere decir que por mucho que los demás ingredientes sobran, Tom no puede hacer más de 5 pasteles porque no dispone de la harina suficiente para ello.
2.- Desigualdad: Tom quiere asegurarse de tener suficiente azúcar para satisfacer las necesidades de su pastel de chocolate. También sabe que cada pastel necesita 1 taza de azúcar y tiene 8 tazas de azúcar disponibles. También sabe que quiere hacer al menos 6 pasteles.
Tom quiere comprobar si puede hacer al menos 6 pasteles con sus ingredientes, en base al azúcar la desigualdad se convierte en x ≤ 8 y x ≥ 6, lo cual se puede combinar en:
6 ≤ x ≤ 8
Lo anterior significa que Tom teóricamente puede preparar entre 6 y 8 pasteles si todos los ingredientes son suficientes.
Conclusión: Si Tom quiere hacer al menos 6 pasteles, necesitará entre 6 tazas de azúcar y 8 tazas de azúcar.
Escenario: Número de galones que necesita Ashley.
Supongamos que hay una persona llamada Ashley que está planeando un viaje por carretera desde la ciudad A a la ciudad B. Si hablo de la distancia entre dos ciudades, entonces es de alrededor de 240 millas. El tanque de combustible del automóvil de Ashley tiene capacidad para contener 12 galones de Supongamos que su automóvil recorre 20 millas por cada galón, entonces, ¿cuántos galones de gasolina puede comprar Ashley si ya tiene 2 galones en su tanque y quiere tener un mínimo de 1 galón restante cuando llegue a la ciudad B?
| Distancia entre A y B | 240 millas |
|---|---|
| Capacidad | 12 galones |
| Kilometraje | 20 millas por galón |
| Disponible tanque de gasolina: Ashley | 2 galones |
| Mínimo combustible sobrante en B | 1 galón |
Primeramente, para recorrer la distancia total de 240 millas, se debe calcular la cantidad total de combustible necesaria, para ello se divide la distancia total por el número de millas recorridas por galón:
240 / 20 = 12
Por tanto, la cantidad total de combustible necesaria para realizar el viaje es de 12 galones.
Ashley ya tiene 2 galones en su tanque y desea mantener 1 galón mínimo cuando llegue, esto significa que debe comprar una cantidad suficiente de combustible para alcanzar estos 12 galones necesarios respetando esta restricción, esto lo podemos modelar mediante la desigualdad x+2≥12−1, donde (x) representa la cantidad de galones a comprar.
| Desigualdad | x + 2 ≥ 12 − 1 |
|---|---|
| Se simplifica la desigualdad | x + 2 ≥ 11 |
| El término independiente se pasa al otro lado | x ≥ 11 - 2 |
| Se realiza la resta | x ≥ 9 |
Conclusión: Ashley debe comprar al menos 9 galones para completar su viaje, manteniendo 1 galón en su tanque cuando llegue, esto asegura que tendrá un total de (2 + 9 = 11) galones, lo cual es suficiente para cubrir la distancia de 240 millas respetando sus necesidades, esta solución tiene en cuenta sus limitaciones y optimiza el uso de su combustible.

Gustoso de presentar mi participación en este concurso; aprovecho la oportunidad de invitar a @graceleon, @fjjrg y @naka05 a que participen en esta actividad:
Steemit Learning Challenge Season 22 Week 2//Equations and inequalities
Las imágenes son de mi propiedad, tomadas con Infinix Note 40 Pro.
Cc: @khursheedanwar
¡Saludos y bendiciones!
