SLC-S22W1/Variables and Expressions by @sabbirakib
Hello everyone, how are you? I hope you are fine and doing well. Today I am going to participate in the algebra lesson by our beloved Professor @khursheedanwar. With this post, I am participating in Steemit Learning season 22, week 1.

| Task 1 |
|---|
| Explain any two variables and expressions types other than that which are explained in this course. |
Variables
Variables are symbols used in Algebra to determine a value that can be changed or modified and replaceable.
Expression
Expression is a group of mathematical operations, variables, and constants that are used in a manner that can be useful.
Let's discuss two types of variables which is not explained in our class.
- Qualitative variables:
There are variables called qualitative variables. Qualitative variables are the kind of variables that can't presented by numbers. It refers to name, level, etc, which are not numbers.
For example
Who is the president of the club?
Algebraic Example
The students of the school ride an 'X'-colored bus. Here, X is the qualitative variable that can not be presented as numbers. Instead, it will provide information on the name of the color.
- Quantitative variables:
Quantitative variables are those variables that can be presented by numbers.
For example
How many students does that school have?
Algebraic example
In the 'X'-colored buses, Y number of students traveled. Here, X is a qualitative variable, and Y is a quantitative variable, which is a number.
More specifically: Y number of students traveled by X-colored bus.
| Task 2 |
|---|
| Show your way of evaluating of an algebraic expression if values of variables are given? Step by step explanation required! |
If there is the value of variables is given I will follow the PEMDAS rules. Where I will go for parentheses first if there are any parentheses left. After that, I will go for exponents. Later on, I will complete the multiplication and then complete the division if there are any. Then, I will solve the addition first and then the subtraction.
Let's demonstrate with the equation we discussed In task 1. There are three colors of the bus in that college. Name them X, Y, and Z. On the X bus, several students travel every day. In the Y bus, the number of students traveling is double that of the X bus. In the Z bus, the number of students traveling is half that of the X bus. The given value of X bus, a total of 20 students traveling every day. The question is, how many students of that college travel by bus every day?
Let's consider the number of X bus students is = a.
X = a.
So, Y bus student is =2a (Double of X)
Y = 2a
So, Z bus student is = 1/2×a (Half of X)
Z = 1/2×a
The total number of students traveling by bus is,
X + Y + Z
= a + 2a + 1/2×a (Value of X, Y, and Z).
= (2a+4a+a)/2
= 7a/2
= 7×20÷2 [20 is the value of a]
= 140÷2
= 70
So, the answer is that 70 students travel by bus every day.
| Task 3 |
|---|
Simplify this expression: 3(2x - 1) + 2(x + 4) - 5
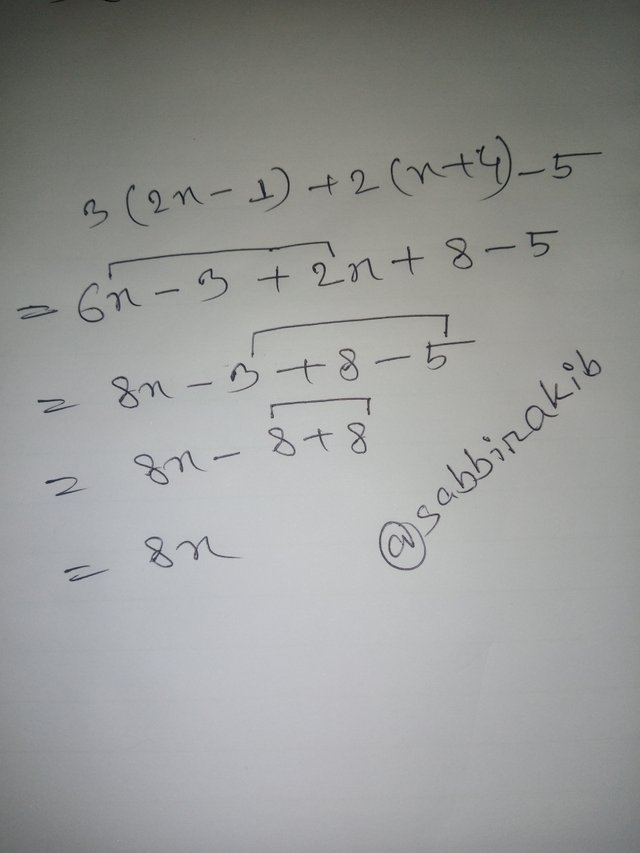
According to PEMDAS, parentheses should be clear first. So, I multiplied that and cleared the parentheses.
Here, I did -3 and -5 first, which seems like I didn’t obey the PEMDAS rules. But it’s not like that. It's an addition. Addition of subtraction.
Evaluate this expression: (x2 + 2x - 3) / (x + 1) when x = 2

Here, x2 means, x multiple x. It’s not (x+x). It is (x multiple x).
Here, I go with exponents first. In the same-line multiplication, I thought it wouldn't be a problem. I just skipped one more line. Then I went for addition, and then I went for subtraction, and the final result came out.
Solve the following equation: 2x + 5 = 3(x - 2) + 1
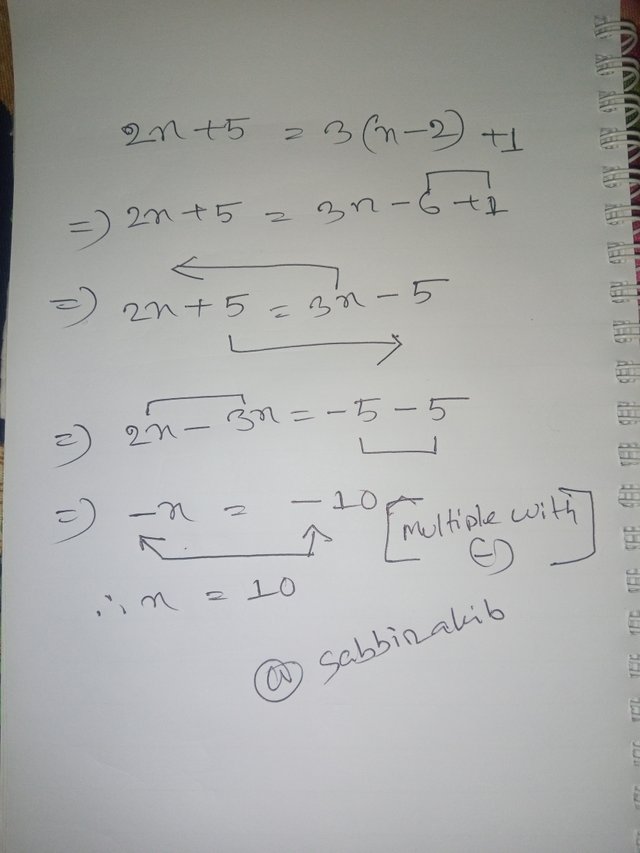
Here, I cleared the parentheses first and then went for subtraction on the right side. In the very next line, I changed the side of matching variables. Subtraction on both sides was multiple with (-), so the value remained the same, but we got an accurate result.
| Task 4 |
|---|
- Solving the Bakery question:
The company sells 250 loaves of bread per day, whereas the 'X' number of bread is white bread. And, wheat bread is 30 more than white bread. So, the total number of wheat breads is (X+30).
The expression will be:
X + (X+30)= 250 [Equation no.1]
The company makes a $0.50 profit per white bread a day. So, the total profit from white bread will be = $(0.50×X)
The company makes a $0.75 profit per wheat bread a day. So, the total profit from wheat bread will be = ${0.75×(X+30)}
So, the company's total profit from white bread and wheat bread combined will be,
= ${0.50×X+0.75×(X+30)} [Equation no. 2]
We can figure out the value of x from equation no.1.
Let's do it.
X+(X+30)=250
=> X + X + 30 = 250
=> 2X + 30 = 250
=> 2X = 250-30
=> 2X = 220
=> X = 220/2
.•. X = 110
Let's find out the total profit of the company from equation no.2 with the value of X we just find out.
${0.50×110+0.75×(110+30)}
=$(55+0.75×140)
=$(55+105)
=$160
The company makes $160 per day from their 250 loaves of bread.
- Solving the Rent-A-Car problem
The situation is the cost of renting a car from that company is $(2x+15). Where X represents hours of rent. 2 is a constant that won't change, and X is a variable that can change. 15 is also a constant that stands for an additional cost. This is a simple equation/expression stands.
The rental company comes with an offer that if someone rents a car for more than 4 hours, the cost will be $(3X-2). There, 3 is constant, and X is variable. 2 is a subtraction constant. But, there is a condition applied, which is the value of X should be >4.
So, the expression stands: $(3X-2) if X>4.
And : $(2X+15) if X<4.

I would like to invite @kibreay001, @impersonal, and @mostofajaman bhai to participate.
My Twitter Promo Link : https://x.com/akib_66/status/1869462602780496361?t=s8HfmNhW05pqUHB8vPQjmQ&s=19
@tipu curate
;) Holisss...
--
This is a manual curation from the @tipU Curation Project.
Upvoted 👌 (Mana: 4/8) Get profit votes with @tipU :)
Thank you very much for inviting me to participate. I will try to participate from my place.
Wish you all the best.