We will create a Scilab program that will allow us to easily change values of R using the input('statement'); function. Then, write the a program to implement the steps in conducting transient analysis. Now, we write a code that enables to accept values of R, L, and C.
R1=input('Enter value of R1 in ohms:');
R2=input('Enter value of R2 in ohms:');
L=input('Enter value of L in Henry:');
C=input('Enter value of C in Farad:');
Vs=input('Enter value of source voltage (Vs) in volts');
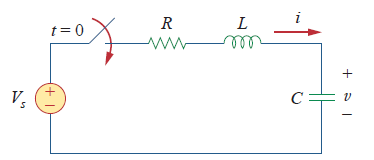
In determining the circuit's transient response, we need to determine the initial values of current (Io) and voltage (Vo). Io is equal to the current experience between all connected resistor as to the voltage (Vs ) applied to the circuit, while Vo is the voltage across R2 when switch is flipped at t>0. So we write the code as:
Io = Vs/(R1+R2); //initial current value
Vo = R2(Io); //initial voltage value
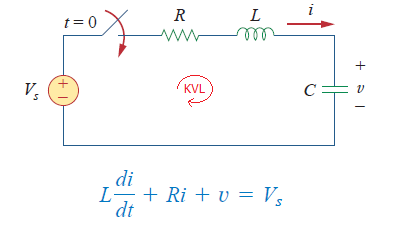
Next, we will determine the transient condition of the circuit either it is overdamped, underdamped, or critically-damped. We will determine characteristic root a = 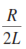 and w0 = and w0 = 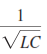 for t > 0. Take note that the value to be used in the equation stated earlier ar R1, L, and C. To be able to take the square root of a function or a number, use the for t > 0. Take note that the value to be used in the equation stated earlier ar R1, L, and C. To be able to take the square root of a function or a number, use the sqrt() in Scilab. The following conditions will determine the transient response of the circuit:
1. when a > w0, the circuit is overdamped;
2. when a < w0, the circuit is underdamped; and,
3. when a = w0, the circuit is critically damped.
We start by solving the value of a and w0.
a=R1/(2*L); // coefficient a
w0=1/sqrt(L*C); //coefficient w0
Using if and elseif function, we will create a program that will implement the conditions stated earlier. Inside the if() and elseif() function, we will have the different mathematical operations and analysis for each of the condition stated. We will also use the equation derive in the the prior section of this text.
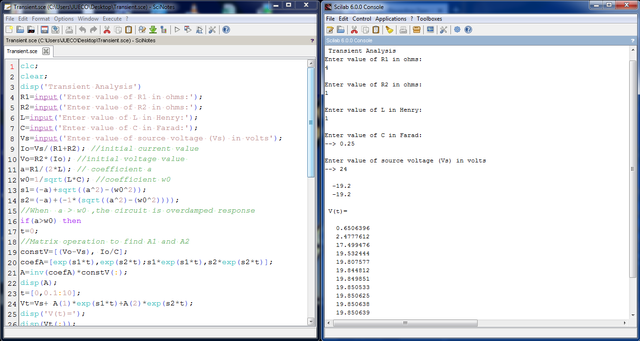
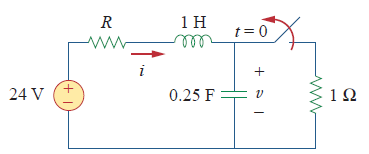
Case 1: When R = 5 ohms. For t < 0, the switch is closed for a long time by which capacitors behaves like open circuit while inductor acts like a short circuit.
For case1, we initialize a condition for overdamped response of the circuit which is characterize by a > w0. Inside the if function, we will implement the derive equation for overdamped response and the derivative of this equation.
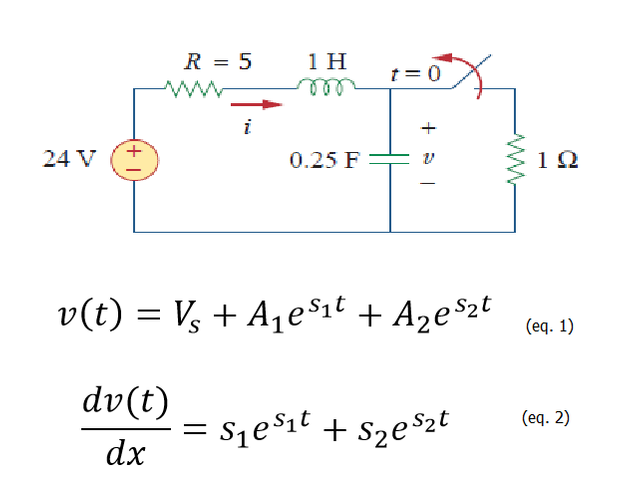
To be able to solve the value of v(t), we need to manipulate the equations to solve for A1 and A2. However, it will become more complicated if we try to use subtitution or elimination technique in our program implementation. So, we will use the matrix functionality to solve the values for A1 and A2. So, we write the code as:
if(a>w0) then
t=0;
//Matrix operation to find A1 and A2
constV=[(Vo-Vs), Io/C];
coefA=[exp(s1*t),exp(s2*t);s1*exp(s1*t),s2*exp(s2*t)];
A=inv(coefA)*constV(:);
Next, we include a code. The program above is derive from this simplified matrix taken from the equation stated earlier.
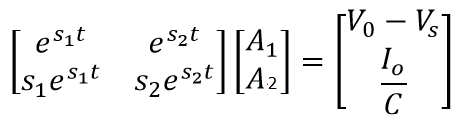
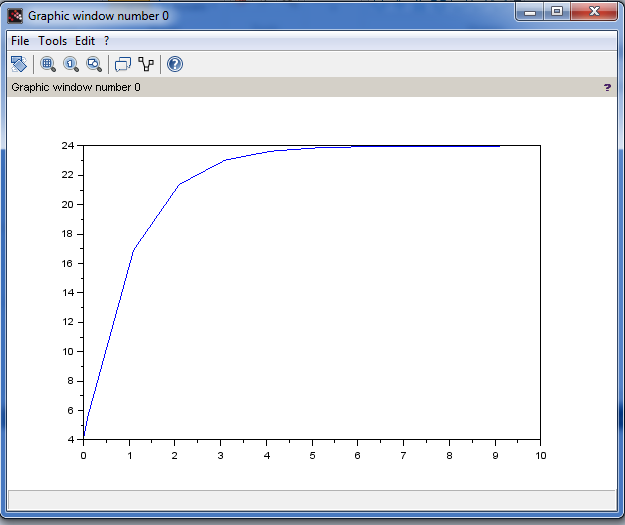
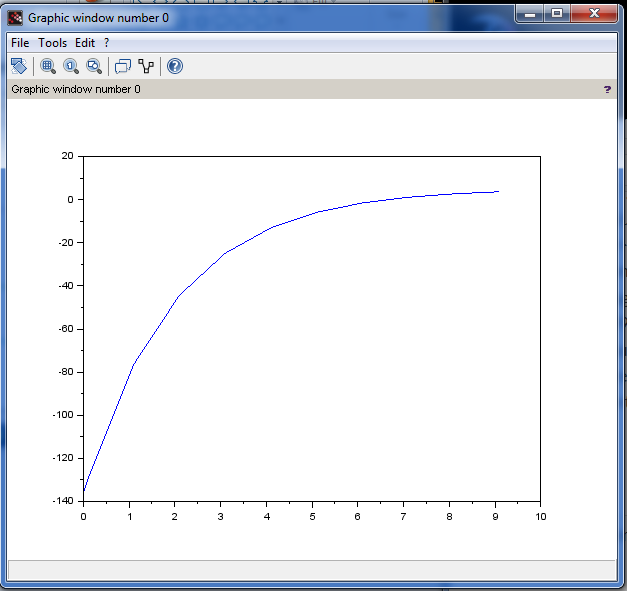
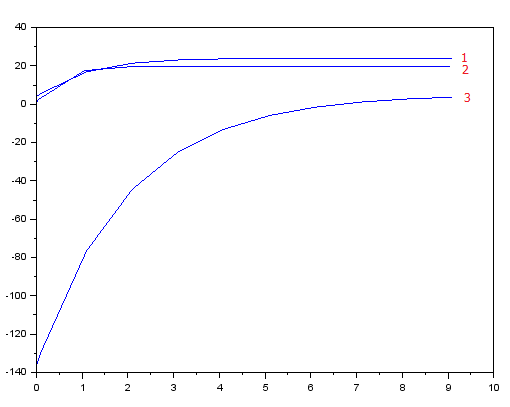
To finalize all operation for case 1, we will need to implement a code that will allow as to plot v(t) as a function of time as 0 < t < 10 sec with plot step of 0.1.
disp(A);
t=[0,0.1:10];
Vt=Vs+ A(1)*exp(s1*t)+A(2)*exp(s2*t);
disp('V(t)=');
disp(Vt(:));
plot(t,Vt);
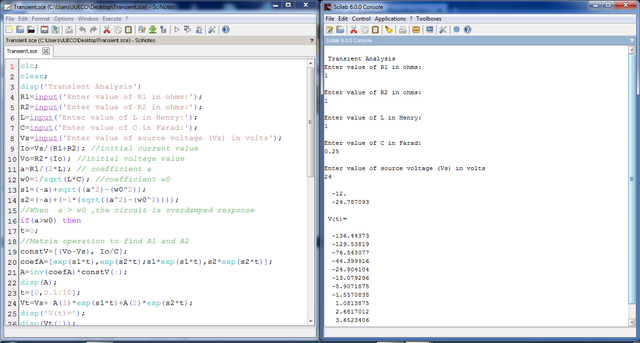
Case 2: When R = 4 ohms. For t < 0, the switch is closed for a long time by which capacitors behaves like open circuit while inductor acts like a short circuit. For case2, we initialize a condition for critically-damped response of the circuit which is characterize by a = w0. We will continue by using elseif() function.
//When a = w0 ,the circuit is critically-damped response
elseif(a==w0) then
t=0;
//Matrix operation to find A1 and A2
constV=[(Vo-Vs), Io/C];
coefA=[exp(-a*t),(t*exp(-a*t));(-a*exp(-a*t)),1];
A=inv(coefA)*constV(:);
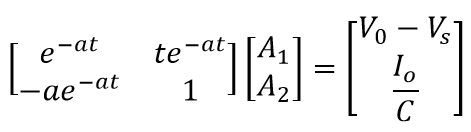
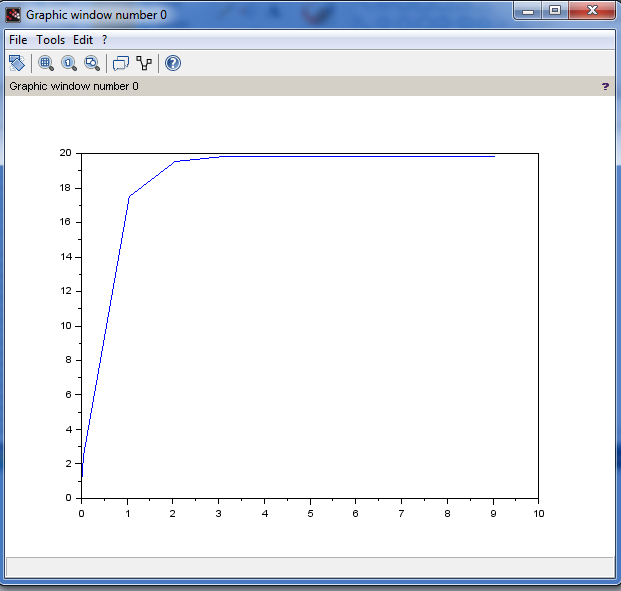
This time the matrix of equation that we will be manipulating in the code is shown above. Instead of using s1 and s2, we will using the characteristic root a hence at critically-damped response, the circuit is in resonance. Next, we will plot and display the value of v(t) at a t is equal to 0 < t <10.
disp(A);
t=[0,0.05:10];
Vt=Vs+A(1)*exp(-a*t)+A(2)*t*(exp(-a*t)(:));
disp('V(t)=');
disp(Vt(:));
plot(t,Vt);
For the voltage Vt=Vs+A(1)*exp(-a*t)+A(2)*t*(exp(-a*t)(:)); plot equation, directly multiplying matrix with different number of rows and columns results to an error so you need to determine when to transpose the matrix. For instance, multiplying A(2)*t results to 1x10 matrix which could not be multiplied directly to an identical 1x10 matrix at the result of exp(-a*t). So, we need to transpose the last part of the equation: (exp(-a*t)(:).
Case 3: We will still be using the same circuit but now will consider R = 1 ohms in building our program. For case 3, we will identify the underdamped response of the circuit that will satisfy a < w0.
//When a > w0 ,the circuit is underdamped response
elseif(a<w0) then
t=0;
//Matrix operation to find A1 and A2
wd=imag(s2);
constV=[(Vo-Vs), Io/C];
coefA=[cos(wd*t)*exp(-a*t),t*sin(wd*t)*exp(-a*t);
exp(-a*t)*wd*sin(wd*t),exp(-a*t)*wd*cos(wd*t)];
A=inv(coefA)*constV(:);
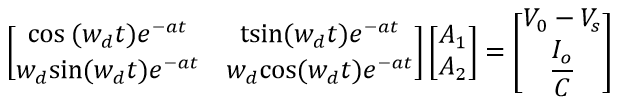 Thw prior cases, only involves Vt as an exponential function of t. For this case, we will involve trigonometric functions such as Thw prior cases, only involves Vt as an exponential function of t. For this case, we will involve trigonometric functions such as sin() and cos(). In addition, since the underdamped response of a circuit involves the complex properties of the circuit response, we also use imag() to call out the imaginary properties of the characteristic root a. Then, we write a code to display and plot the underdamped response as a function Vt at t < 10.
disp(A);
t=[0,0.1:10];
Vt=Vs+A(1)*cos(wd*t)*exp(-a*t)(:)+A(2)*t*sin(wd*t)(:)*exp(-a*t);
disp('V(t)=');
disp(Vt(:));
plot(t,Vt);
end
In addition, we will also use matrix transpose to be able to perform multiplication of matrix which i have discuss earlier in case 2. Here is the code in the SciNotes.
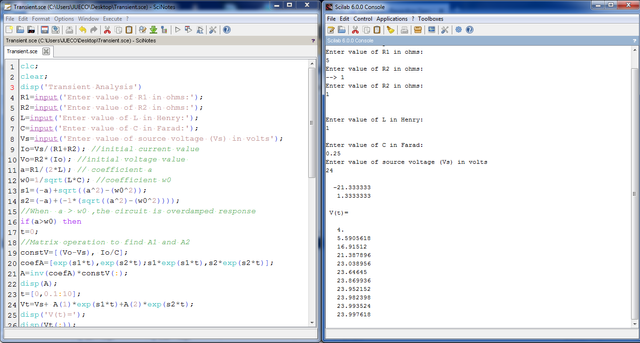
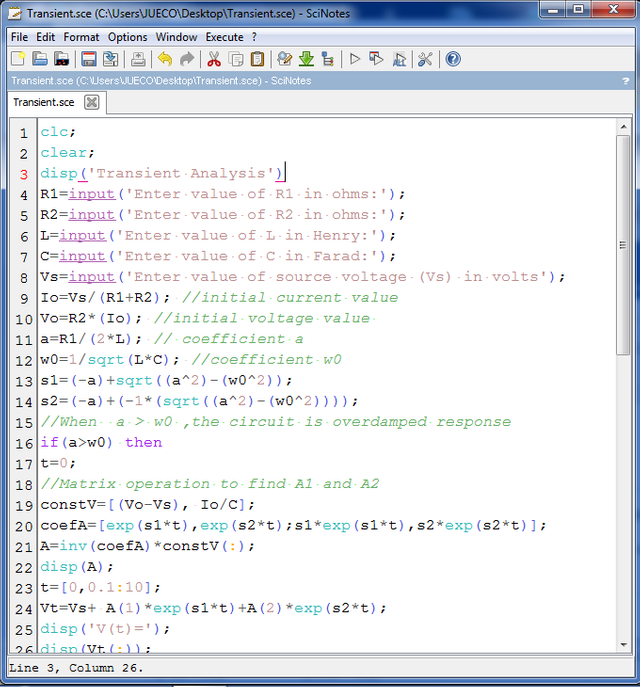 |


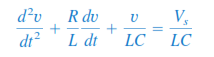
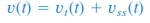
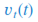
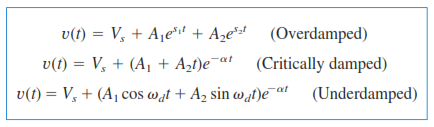
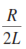
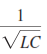

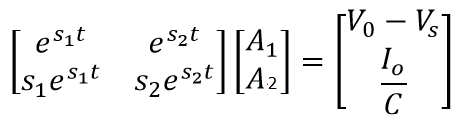
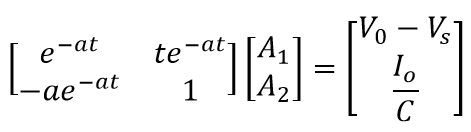
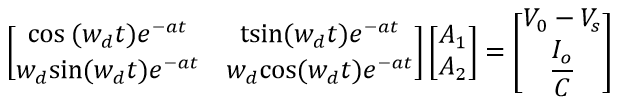

Congratulations! This post has been upvoted by the communal account, @steemph.cebu by juecoree being run at Teenvestors Cebu (Road to Financial Freedom Channel). This service is exclusive to Steemians following the Steemph.cebu trail at Steemauto. Thank you for following Steemph.cebu curation trail!
Don't forget to join Steem PH Discord Server, our Discord Server for Philippines.
Thanks for sharing your learnings... We never done that before😣 Performing such activity will help students to understand more behind its behavior. Through experiments and tests, students will broad their knowledge in a certain topic😊
Hi @dapmonylia ! I am glad it helps you. Yes, hand-on activities is very essential in learning basic and advance circuit theory. Appreciated! Cheers!
Thank you for the contribution. It has been approved.
You can contact us on Discord.
[utopian-moderator]
Thanks @laxam
Hey @juecoree I am @utopian-io. I have just upvoted you!
Achievements
Community-Driven Witness!
I am the first and only Steem Community-Driven Witness. Participate on Discord. Lets GROW TOGETHER!
Up-vote this comment to grow my power and help Open Source contributions like this one. Want to chat? Join me on Discord https://discord.gg/Pc8HG9x