Quantum Computers - Qubit Architecture

Hey Steem people! This is one of my first posts on a topic I think most of you find interesting. There has been a lot of talk about the advent of the quantum computer and the shakeup of cryptography.
First off, the computer you are using is built from binary transistors. A bit is an electric signal that can either be on or off. Electricity flows through a circuit and can be turned on or off. In a way, off means false and on means true, which will be useful for a number of applications. We usually describe a bit by a 0 or a 1 (0 being the off and 1 being on). So in a binary computer, also called a classical computer, every bit either has a state of 0 or 1 and there are no other states.

Step into the quantum world and there are physical systems or switches that can be both on AND off simultaneously. A qubit is a unit of information that describes a 2-dimensional system. Binary systems are 1-dimensional. A single qubit, or a single quantum system, can be in a 0 and 1 state at the same time. Qubits are represented with a 2x1 matrix with complex numbers. I'll explain complex numbers from a quantum computing perspective in another post. Here's the usual notation for a qubit:

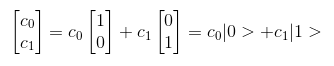
If you square c0 then you will get the probability of finding the qubit in state 0 upon physical measurement. Likewise, if you square c1 then you get the probability of finding the qubit in state 1.
Weirdly, whenever we look at or measure a qubit, it becomes a bit. Our simple act of being observers "collapses" the quantum world. I'll explain the reason behind this in another post.
Notice that 2 qubits are the canonical basis for the Complex Number Space with 2-dimension. So any non-zero element of this space can be turned into a qubit.
I know you're saying, "Sounds great, but how do we build a qubit?"
There are three ways I am aware of.
First, we can take advantage of the fact that an electron in an atom might be in one of the two energy levels, either ground state or excited state.

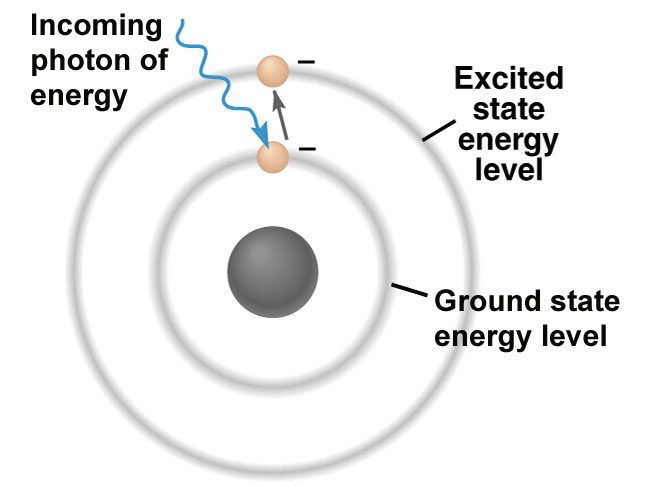
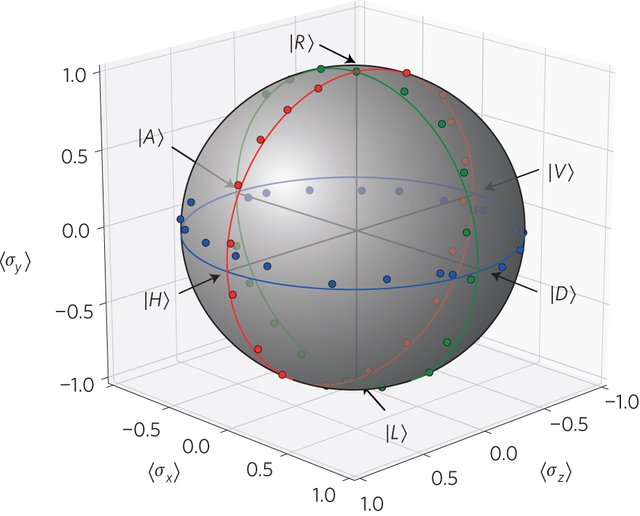
Second, since a photon can be in either one or two different polarized states, we can use that as well.

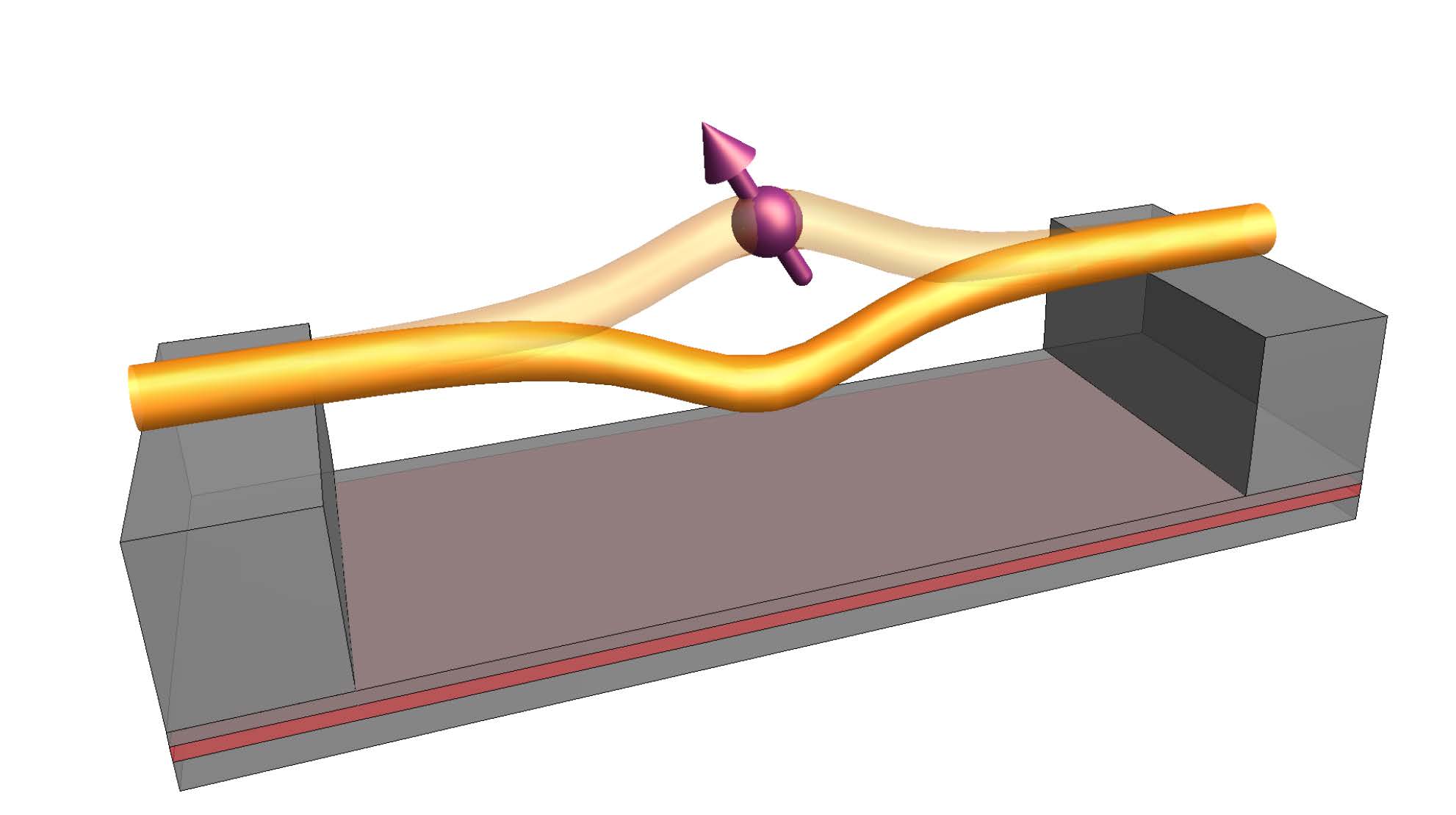
Thirdly, many subatomic particles have either one spin direction or another.

So there are physical systems on the quantum level that have this dual state character. We can utilize this to build actual qubits. Remember, however, that when we measure these quantum systems, we will only see one state. But the strange thing of the quantum world is that particles can have different states at the same time... In fancy words, these quantum systems have indeterminacy and superposition effects, meaning we can only measure one state of a particle that has more than one state.
But computers with just one bit, or qubit, are kind of boring. If we had a computer built with 8 qubits than we would have 8 different complex spaces each with 2 dimensions. In math notation:

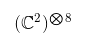
which has a total dimension of 2 to the power of 8 = 256 dimensions. Okay now we might be able to break some codes with a space made out of 256 dimensions! Also, 8 qubits together is called a qubyte. Later I'll go into how we build electrical circuits and briefly how to do that on the micro and nano level, which are basically gates (either open or closed). Then I'll describe the possibilities with quantum gates.

CONCLUSION
Instead of building computers with electrical switches, we can build them out of electrons, photons, or various subatomic particles. Currently there are some quantum computers with as many as 84 qubits and that number will grow as our engineering gets better. I believe that Stanford University owns a quantum computer that takes up about 500 square feet, but I haven't been there yet.
If you are interested in this topic than stay tuned for more. Also, check out @omar-hesham and his videos. He has really good videos on electronics, computers, cryptocurrency, and related stuff like do-it-yourself projects.