Calculating the distance between planets and celestial bodies in the field of Physics

Greetings to all lovers of science, physics, and the rest of the universe. Today, the vastness of space has always sparked people's interest. One of the basic questions in space science and physics is how to measure the space between celestial objects, such as planets, stars, or galaxies.

This calculation is crucial not only for understanding the cosmic framework, but also for organizing space expeditions and examining celestial events. Physics, under the umbrella of mathematical and observational tools, offers the most accurate ways to measure these vast distances.

One of the earliest and most basic techniques is the trigonometric parallelogram, based on the concept of triangulation. When viewing a star from two separate points in Earth's path (about six months apart), a small change in angle occurs.

Using trigonometry and the common distance between viewing spots (the width of Earth's orbit), the star's distance can be determined. This method works well for nearby objects, such as stars that are a few hundred years away.

The basic formula used in this method is:

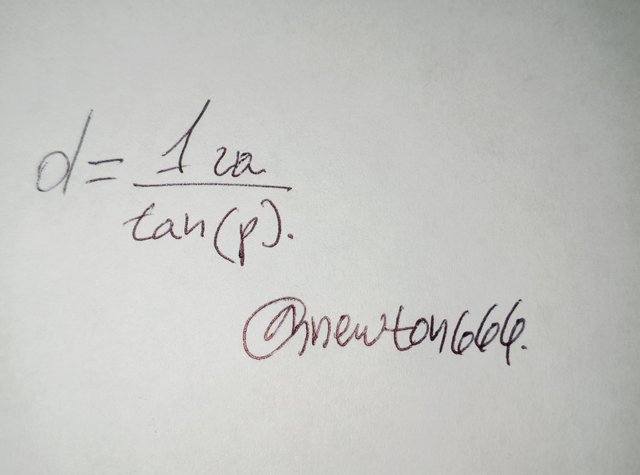
Where d is the distance to the object, p is the parallax angle in radians, and 1 au (astronomical unit) is the average distance between the Earth and the Sun (approximately 149.6 million km).

For distant objects, different physical and space science techniques are applied, such as the change in the color of light (redshift). When a star moves away from us, its light shifts toward the red part of the light spectrum. What is unique in this case is that this occurrence, explained by the Doppler shift, can be measured to calculate the retreating velocity of a galaxy. If the Hubble constant is determined, Hubble's law can be applied to calculate the distance.

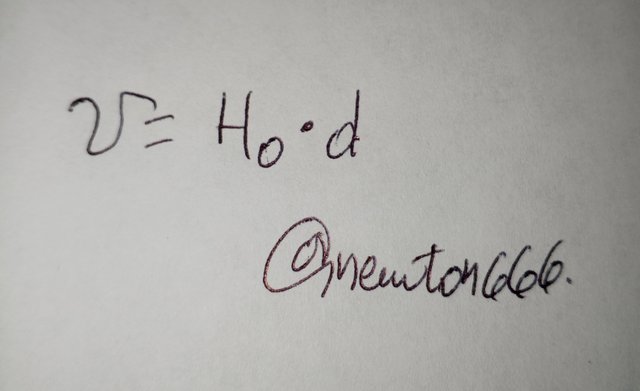
Where v is the speed at which the object is receding (determined by the redshift), and D is the separation. This technique is highly beneficial in astronomy for measuring the space between American galaxies and distant ones, which can be millions or billions of light-years across.

Another technique used in the solar system is radar. Through radio waves transmitted to nearby planets like Venus or Mars, the echo's return time to Earth is measured. Since the brightness of the light is stable, the distance can be determined with the equation

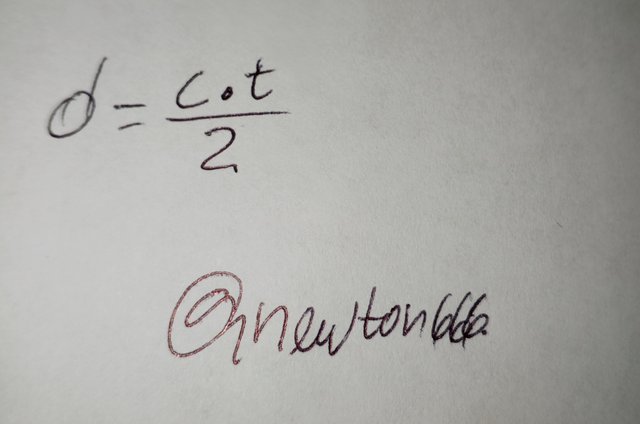
Where c is the speed of light (approximately 3 x 10^8m/s), and t is the time it takes for the signal to travel there and back. This is one of the most accurate methods for measuring distances within the solar system.

Calculating distances between celestial bodies is a complex task, there's no doubt about it. It requires in-depth physical principles, hard mathematical laws, and, my dear readers, some very advanced technological tools. With simple parallax trigonometry and, oh!, spectroscopic redshift analysis, physics has allowed humans to peer deeply into the universe.

Now you know the positions of the stars, but also their motion, evolution, and those mysteries, since these calculations not only situate us in space, they also link us to history and the destiny of the cosmos.

Bibliographic Reference

Universal Natural History and Theory of Heaven by Immanuel Kant, 2024.

Determination of some fundamental physical constants without complex equipment by Velasco Maíllo, Santiago, ‎Mazo Vivar, Alejandro del, 2024.

General Physics by Pérez Montiel, Héctor, 2020