31-03-2025 - Education - Euclidean scalar product [EN]-[IT]

Cover background image generated with AI, software used: copilot microsoft

---

~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~

---

[ENGLISH]
31-03-2025 - Education - Euclidean scalar product [EN]-[IT]

Image generated with AI, Microsoft Copilot

With this post I would like to provide some brief notions about the topic mentioned in the subject.
The context in which we operate is that of Analytic Geometry
(code notes: MOD-66)

Euclidean scalar product
Introduction
The Euclidean scalar product is essentially an operation that takes place in linear algebra or in analytical geometry.
In Euclidean geometry (and also in physics) it is common to use another notion of scalar product, which is equivalent to the standard one.

Definition
The Euclidean scalar product between two vectors a and b in Euclidean space is defined as follows:
a * b = a1b1 + a2b2 +...+anbn

Where:
a = (a1,a2,...,an) and b = (b1,b2,...,bn) are vectors in Rn

What are the properties of the Euclidean scalar product?
-Commutative property: a * b = b * a
-Distributive property: a * (b+c) = a * b + a * c
-Associative property with respect to scalar multiplication: K (a * b) = (ka) * b = a * (kb)

Geometric interpretation
The Euclidean scalar product has its own geometric interpretation.
It can be expressed as follows:

Where:
∥a∥ and ∥b∥ = the lengths of vectors a and b
θ = the angle between the two vectors

Standard Dot Product
The standard dot product is simply the Euclidean dot product, it just has one different term.
Both describe the process of taking two vectors in Euclidean space and calculating a single number (also called a scalar) by adding the products of their corresponding components.
So the formula is always the same. I repeat it below for ease of reading:

Angles in Euclidean vector spaces
Let's try to give a purely technical definition.
In a Euclidean vector space, the angle between two vectors a and b is defined by using the scalar product, where the formula for calculating the cosine of the angle θ between the two vectors is as follows:

cos(θ) = (a * b) / ∥a∥ ∥b∥

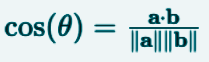
Where:
a and b = the scalar product of vectors a and b
∥a∥ and ∥b∥ = the lengths of vectors a and b

Conclusions
The Euclidean scalar product and angles in Euclidean spaces, in addition to technical subjects such as physics, find application in computer graphics and navigation.

Question
Did you know that the calculation of navigation routes is done by calculating the Euclidean scalar product and the angles in Euclidean spaces?

---

---

[ITALIAN]
31-03-2025 - Education - Prodotto scalare euclideo [EN]-[IT]

Immagine generata con IA, Microsoft Copilot

Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento citato in oggetto.
Il contesto in cui operiamo è quello della Geometria analitica
(code notes: MOD-66)

Prodotto scalare euclideo
Introduzione
Il prodotto scalare euclideo sostanzialmente è un'operazione che si volge in algebra lineare o in geometria analitica.
Nella geometria euclidea (e anche in fisica) è consueto utilizzare un’altra nozione di prodotto scalare, che è equivalente a quella standard.

Definizione
Il prodotto scalare euclideo tra due vettori a e b nello spazio euclideo è definito come segue:
a * b = a1b1 + a2b2 +...+anbn

Dove:
a = (a1,a2,...,an) e b = (b1,b2,...,bn) sono vettori in Rn

Quali sono le proprietà del prodotto scalare euclideo?
-Proprietà commutativa: a * b = b * a
-Proprietà distributiva: a * (b+c) = a * b + a * c
-Proprietà associativa rispetto alla moltiplicazione scalare: K (a * b) = (ka) * b = a * (kb)

Interpretazione geometrica
Il prodotto scalare euclideo ha una sua interpretazione geometrica.
Esso può essere espresso nella seguente maniera:

Dove:
∥a∥ e ∥b∥ = le lunghezze dei vettori a e b
θ = l'angolo tra i due vettori

Prodotto scalare standard
Il prodotto scalare standard è semplicemente il prodotto scalare euclideo, ha solo un termine diverso.
Entrambi descrivono il processo di prendere due vettori nello spazio euclideo e calcolare un singolo numero (detto anche uno scalare) attraverso la somma dei prodotti delle loro componenti corrispondenti.
Quindi la formula è sempre la stessa. La ripeto qui sotto per comodità di lettura:

Angoli negli spazi vettoriali euclidei
Proviamo a darne una definizione prettamente tecnica.
In uno spazio vettoriale euclideo, l'angolo tra due vettori a e b viene definito tramite l'utilizzo del prodotto scalare, dove la formula per calcolare il coseno dell'angolo θ tra i due vettori è la seguente:

cos(θ) = (a * b) / ∥a∥ ∥b∥

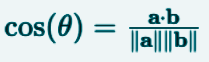
Dove:
a e b = il prodotto scalare dei vettori a e b
∥a∥ e ∥b∥ = le lunghezze dei vettori a e b

Conclusioni
Il prodotto scalare euclideo e gli angoli negli spazi euclidei, oltre che in materie tecniche come la fisica, trovano applicazione nella grafica computerizzata e nella navigazione.

Domanda
Lo sapevate che il calcolo delle rotte di navigazione viene fatto calcolando il prodotto scalare euclideo e degli angoli negli spazi euclidei?

THE END