29-09-2025 - Exercise - Linear Programming and the Simplex [EN]-[IT]
Cover background image generated with AI, software used: copilot microsoft
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
29-09-2025 - Exercise - Linear Programming and the Simplex [EN]-[IT]
[IMAGE]
Image generated with AI, Microsoft Copilot
With this post, I would like to provide some brief insights into the topic mentioned above by completing some exercises.
The context in which we operate is Operations Research
(lesson/article code: MS_12)
Linear Programming and the Simplex
Here we are, tackling a rather difficult topic.
Linear programming is a mathematical method used to solve maximization and minimization problems by seeking the optimal solution. The simplex method is an algorithm that, when applied to the development of a linear programming problem, helps solve highly complex problems.
Without the simplex method, some linear programming problems related to logistics or product production would be difficult to solve or would take an enormous amount of time.
Exercise
Let's take the following exercise as an example:
Objective
Constraints
Starting the Exercise
The first thing to do is transform the problem into standard form by introducing the slack variables.
After doing this, our problem will appear as in the image below.
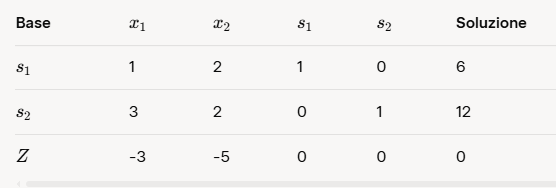
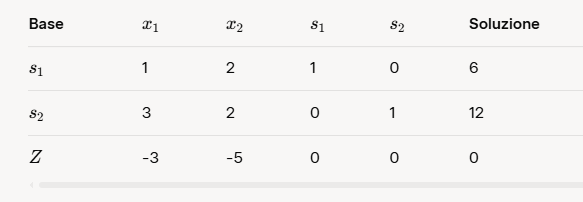
Now let's create and populate the initial simplex table.
The Entering Variable
Let's specify that since this is a maximization problem, in the tableau at row Z, both x1 and x2 will change sign and become negative. This is standard practice for a maximization problem. Indeed, we see that in row Z, x1 becomes -3 and x2 becomes -5.
At this point, we need to choose the entering and exiting variables.
To do this, we simply follow a rule.
The entering variable is x2 because, between x1 and x2, the variable with the most negative coefficient is precisely x2.
Then we calculate the minimum ratio.
The entering variable is x2, because it has the most negative coefficient in row Z(-5).
To choose the exiting variable, we calculate the ratio between the known term and the coefficient of the entering variable in the row.
Row 1
For row 1, the known term is 6, the coefficient of x2 is 2, so the ratio is 6/2=3
Row 2
For row 2, the known term is 12, the coefficient of x2 is 2, so the ratio is 12/2=6
The minimum ratio is 3, so the outgoing variable is s1, so the pivot row is s1
The PIVOT Element
The pivot element is the element at the intersection of the pivot column (x2) and the pivot row (s1). In the initial table, this is 2.
First Tableau Transformation
Now we need to divide the pivot row by the pivot element.
The Tableau will transform as follows:
Continuation
For now, I'll stop here because the calculations are repeated, but if the procedure from here on is unclear, I'll make a new post explaining the intermediate steps in more detail.
Result
After the various steps, we will have:
x1=0
x2=3
Z=3(0)+5(3)=15
Conclusions
This calculation method is used in production planning, inventory management, and material sourcing. This method eliminates inefficiencies because it can find the optimal solution in a very broad context of choices.
Question
Have you ever heard of the simplex method? Have you ever faced a maximization problem in school?

[ITALIAN]
29-09-2025 - Esercizio - Programmazione lineare e il simplesso [EN]-[IT]
[IMMAGINE]
Immagine generata con IA, Microsoft Copilot
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento citato in oggetto svolgendo degli esercizi.
Il contesto in cui operiamo è quello della Ricerca Operativa
(codice lezione/articolo: MS_12)
Programmazione lineare e il simplesso
Eccoci qua ad affrontare un argomento piuttosto difficile.
La programmazione lineare è un metodo matematico che viene usato per risolvere problemi di massimizzazione e minimizzazione cercando la soluzione ottimale. Il metodo del simplesso è un algoritmo che applicato allo sviluppo di un problema di programmazione lineare aiuta a risolvere problemi di grossa complessità.
Senza il metodo del simplesso, alcuni problemi di programmazione lineare relativi alla logistica o alla produzione di un prodotto sarebbero difficilmente risolvibili o richiederebbero un tempo enorme.
Esercizio
Prendiamo come esempio il seguente esercizio:
Obiettivo
Vincoli
Inizio svolgimento
La prima cosa da fare è trasformare il problema in forma standard introducendo le variabili di slack
Dopo aver fatto questo il nostro problema apparirà come nell'immagine qui sotto riportata.
A questo punto andiamo a creare e a compilare la tabella iniziale del simplesso
La variabile entrante
Specifichiamo che essendo un problema di massimizzazione avremo che nel tableau alla riga Z, sia x1 che x2 cambieranno di segno e diventeranno negativi. Questa è la prassi per un problema di massimizzazione. Vediamo infatti che nella riga Z x1 diventa -3 e x2 diventa -5
A questo punto dobbiamo scegliere la variabile entrante e quella uscente.
Per fare questo basta semplicemente seguire una regola.
La variabile entrante è x2 in quanto tra x1 e x2, la variabile con coefficiente più negativo è proprio x2.
Poi eseguiamo il calcolo del rapporto minimo.
La variabile entrante è x2, perché ha il coefficiente più negativo nella riga Z(-5)
Invece per scegliere la variabile uscente, si calcola il rapporto tra il termine noto e il coefficiente della variabile entrante nella riga.
Riga 1
Per quanto riguarda la riga 1, il termine noto è 6, il coefficiente di x2 è 2, quindi il rapporto è 6/2=3
Riga 2
Per quanto riguarda la riga 2, il termine noto è 12, il coefficiente di x2 è 2, quindi il rapporto è 12/2=6
Il rapporto minimo è 3, quindi la variabile uscente è s1, quindi la riga pivot è s1
L'elemento PIVOT
L'elemento pivot è l'elemento che si trova all'intersezione della colonna pivot (x2) e delle riga pivot (s1). Nella tabella iniziale questo è 2.
Prima trasformazione del tableau
A questo punto bisogna dividere la riga pivot per l'elemento pivot
Il tableau si trasformerà come segue
Continuazione
Attualmente mi fermo qui in quanto i calcoli si ripetono, ma se non è chiara la procedura da qui in avanti, farò un nuovo post dove spiegherò più in dettaglio i passaggi intermedi.
Risultato
Dopo i vari passaggi avremo che:
x1=0
x2=3
Z=3(0)+5(3)=15
Conclusioni
Questo metodo di calcolo viene usato nella pianificazione della produzione, nella gestione delle scorte e nel taglio dei materiali. Con questo metodo si eliminano le inefficienze in quanto è in grado di trovare la soluzione ottimale in un contesto di scelte molto ampio.
Domanda
Avete mai sentito parlare del metodo del simplesso? Avete mai affrontato a scuola un problema di massimizzazione?
THE END

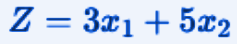
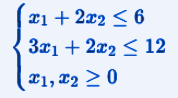
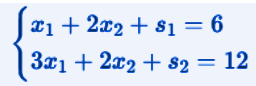

È un metodo che aiuta sia nella programmazione lineare che in quella non lineare, tenendo conto di alcune variabili, è un metodo molto utile.
0.00 SBD,
0.13 STEEM,
0.13 SP
La programmazione lineare può diventare un corso di studio piuttosto ampio, si possono affrontare problemi semplici, di media difficoltà e di grossa difficoltà. Io sudo freddo già con quelli di media difficoltà.
Upvoted! Thank you for supporting witness @jswit.
This post has been upvoted by @italygame witness curation trail
If you like our work and want to support us, please consider to approve our witness
Come and visit Italy Community
Hi! @stefano.massari Great to see you again. This is a really clear and practical explanation of the simplex method . I like how you broke it down step by step, from transforming the problem into standard form, to identifying the entering and exiting variables, and finally reaching the optimal solution. Even though it’s a complex topic, your example makes it much easier to follow. Linear programming really shows its power in real world applications like logistics and production planning. Great work I’d be interested in seeing your next post with the detailed intermediate steps.