11-07-2025 - Exercise - The Simplex Method [EN]-[IT]
Cover background image generated with AI, software used: copilot microsoft
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
11-07-2025 - Exercise - The Simplex Method [EN]-[IT]
Image generated with AI, Microsoft Copilot
With this post, I would like to provide some brief insights into the topic mentioned above by completing some exercises.
The context in which we operate is that of Operations Research
(code notes: MOD-77)
The Simplex Method
Completed Exercise
Below is a linear programming (LP) exercise solved using the simplex method, also providing a graphical explanation of the method itself.
What is the Simplex Method
In operations research, algorithms are used to solve various problems. The simplex method is one of the fundamental algorithms of operations research.
The simplex method, like other algorithms, helps maximize or minimize a linear function subject to linear constraints.
In short, the simplex method is used to find an optimal solution to a linear problem.
It is a deterministic algorithm; it moves from one vertex of the solution polyhedron to another.
It is considered an excellent and quite efficient algorithm; unfortunately, in the worst cases, its complexity expands exponentially.
Description of the method
-Step 1-
It is written in standard form with equality constraints and non-negative variables.
-Step 2-
It starts from a vertex, also called the basic feasible solution, of the solution polyhedron.
-Step 3-
Now we move on to iterations, performing the following operations:
The objective function and the reduced costs are calculated.
An entering variable is chosen.
The exiting variable is determined.
The tableau is updated and a new basis is introduced.
-Step 4-
Finally, when no entering variable can improve the objective function, the optimal solution has essentially been reached.
Example with a specific problem
Let's try to maximize:
With the following constraints:
Below is a graphical example of the simplex method with the problem: given
Image created with artificial intelligence, Microsoft Copilot software
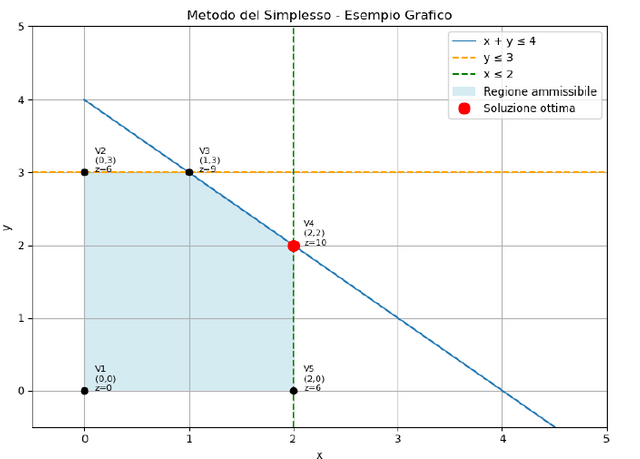
The graph above provides several pieces of information, which I describe below.
The blue area is the feasible region, also called the polyhedron.
The basic solutions are represented by the vertices, the black points.
The optimal solution is represented by the red point. It is (2,2) with z=10.
The simplex moves from one vertex to the next along the edges of the polyhedron, improving z until it reaches the maximum.
The steps of the simplex method shown on the graph
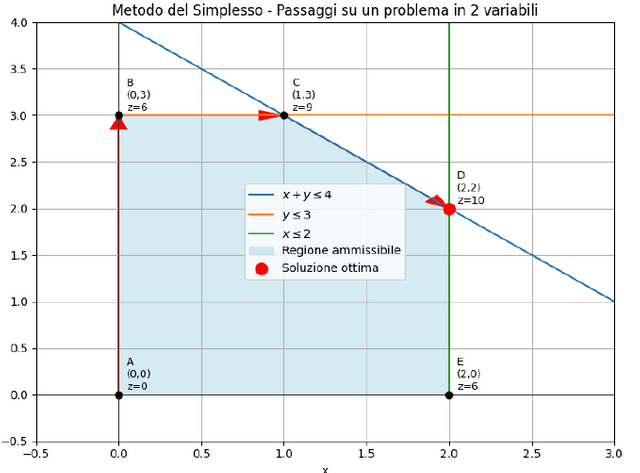
The graph below shows the steps of the simplex method.
The red arrows symbolize the evolutionary path of the simplex method. You can see how, moving from one vertex to the next, the value of Z improves until it reaches its maximum.
Description of the steps.
-Point A (0,0) - starting point where z=0
-Point B (0,3) - point where z improves and reaches 6
-Point C (1,3) - point where z continues to improve and reaches 9
-Point D (2,2) - point representing the optimal solution where z=10
Result
The optimal solution is point (2,2) with z=10
Conclusions
The simplex method is a method used in operations research to solve problems primarily related to profit maximization or cost minimization.
This method is used to find the best solutions in manufacturing, logistics, and resource allocation.
Question
The simplex method was invented by George Dantzig in 1947. Did you know that after Dantzig invented this mathematical method of linear optimization, the same method was applied in economics, engineering, logistics, finance, and industry?

[ITALIAN]
11-07-2025 - Esercizio - Il metodo del simplesso [EN]-[IT]
Immagine generata con IA, Microsoft Copilot
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento citato in oggetto svolgendo degli esercizi.
Il contesto in cui operiamo è quello della Ricerca Operativa
(code notes: MOD-77)
Il metodo del simplesso
Esercizio svolto
Qui di seguito un esercizio di programmazione lineare (PL) risolto con il metodo del simplesso cercando di fornire anche una spiegazione grafica del metodo stesso.
Cosa è il metodo del simplesso
In ricerca operativa, per la risoluzione dei vari problemi, si usano degli algoritmi. Il metodo del simplesso è proprio uno di quegli algoritmi fondamentali della ricerca operativa.
Il metodo del simplesso, come anche altri algoritmi, aiuta a massimizzare o minimizzare una funzione lineare soggetta a vincoli lineari.
In sintesi il metodo del simplesso viene usato per trovare una soluzione ottima di un problema lineare.
Esso è un algoritmo deterministico, si muove da un vertice all’altro del poliedro delle soluzioni.
Viene considerato come un ottimo algoritmo e piuttosto efficiente, purtroppo nei casi peggiori la sua complessità si espande in maniera esponenziale.
Descrizione del metodo
-Passo 1-
Si scrive in forma standard con vincoli di uguaglianza e variabili non negative.
-Passo 2-
Si parte da un vertice, detto anche soluzione di base ammissibile, del poliedro delle soluzioni.
-Passo 3-
Ora si passa alle iterazioni eseguendo le seguenti operazioni:
Si calcola la funzione obiettivo ed i costi ridotti.
Si sceglie una variabile entrante
Si determina la variabile uscente
Si aggiorna il tableau e si passa una nuova base.
-Passo 4-
Infine, quando nessuna variabile entrante può migliorare la funzione obiettivo, praticamente si è giunti alla soluzione ottima.
Esempio con un determinato problema
Proviamo a massimizzare:
Con i seguenti vincoli
Qui di seguito l’esempio grafico del metodo del simplesso con il problema dato
Immagine creata con l’intelligenza artificiale, software Microsoft Copilot
Il grafico qui sopra ci fornisce diverse informazioni, le descrivo qui di seguito.
L’area azzurra è la regione ammissibile, chiamata anche poliedro.
Le soluzioni di base sono rappresentate dai vertici, i punti neri.
La soluzione ottima è rappresentata dal punto rosso. Essa è (2,2) con z=10
Il simplesso si muove da un vertice all’altro lungo i bordi del poliedro, migliorando z fino a raggiungere il massimo.
I passaggi del metodo del simplesso riportati sul grafico
Nel grafico qui sotto sono rappresentati graficamente i passaggi del metodo del simplesso.
Le frecce rosse simboleggiano il percorso evolutivo del metodo del simplesso. Si può notare come muovendosi da un vertice all’altro il valore di Z migliora fino a raggiungere il suo massimo.
Descrizione dei passaggi.
-Punto A (0,0) - punto iniziale dove z=0
-Punto B (0,3) - punto dove z si migliora e va a 6
-Punto C (1,3) - punto dove z continua a migliorarsi e va a 9
-Punto D (2,2) - punto che rappresenta la soluzione ottima dove z=10
Risultato
La soluzione ottima è il punto (2,2) con z=10
Conclusioni
Il metodo del simplesso è un metodo usato in ricerca operativa per risolvere problemi soprattutto legati alla massimizzazione dei profitti o alla minimizzazione dei costi.
Questo metodo viene usato per trovare le soluzioni migliori in ambito produttivo, logistico e delle allocazione delle risorse.
Domanda
Il metodo del simplesso è stato inventato da George Dantzig nel 1947. Lo sapevate che dopo che Dantzig inventò questo metodo matematico di ottimizzazione lineare, lo stesso metodo fu applicato in economia, ingegneria, logistica, finanza, industria?
THE END


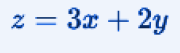
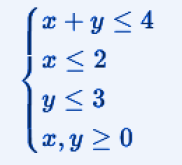
@stefano.massari ,Non vedo il supporto Booming. Saresti così gentile da farmi sapere se non lo stiamo ricevendo? Mi scuso per questa domanda. Ho già chiesto a Italygame e non ho ricevuto risposta. Mi scuso ancora.
L’unica cosa che ti posso dire è che attualmente non ricevo neanche io il supporto booming, ma se viene dato a persone appena entrate mi farebbe piacere perchè andrebbe ad incentivare i giovani utenti. Quando verró a conoscenza del motivo per cui non ricevo il supporto che ricevevo prima, te lo faró sapere. Sono grato del supporto che ho ricevuto fino ad ora. Il non averlo ora non cambierà la mia motivazione.
Sono già stato informato, grazie mille.
Nice information👍🙂
Upvoted! Thank you for supporting witness @jswit.
Thank you for sharing on steem! I'm witness fuli, and I've given you a free upvote. If you'd like to support me, please consider voting at https://steemitwallet.com/~witnesses 🌟