11-06-2025 - Exercise - translational motion and rotational motion [EN]-[IT]
Cover background image generated with AI, software used: copilot microsoft
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
11-06-2025 - Exercise - translational motion and rotational motion [EN]-[IT]
Image generated with AI, Microsoft Copilot
With this post I would like to provide some brief notions about the topic mentioned in the object by doing some exercises.
The context in which we operate is that of Applied Mechanics
(code notes: MOD+10)
translational motion and rotational motion
Exercise 01
Give the definitions of translational motion and rotational motion of a rigid body.
First of all, we can say with certainty that the concept of translational motion and rotational motion of a rigid body are two basic concepts for designing mechanical systems.
Both motions are explained below:
Translational motion
Translational motion of a rigid body is defined when all the points of a rigid body move along trajectories parallel to each other. Using other words, we can say that the relative distance between the points of the body does not change and the orientation of the body remains constant during the motion.
The rigid body can follow trajectories that can be defined by straight lines or trajectories that can be traced back to curves. In the first case, we speak of rectilinear translation, in the second case, we speak of curvilinear translation.
We can schematize the two motions as follows:
Rectilinear motion (translation)
Circular motion (rotation)
Exercise regarding Uniform circular motion
We have a body that moves along a circumference of radius r=2m with constant speed. The body completes a complete turn in T=4s.
Let's try to understand:
-What is the angular velocity ω?
-What is the tangential velocity v?
-What is the centripetal acceleration ac?
-How many revolutions does it make in 1 minute?
the angular velocity ω?
the tangential velocity v
What is the centripetal acceleration ac
How many turns does it make in 1 minute
Exercise 02
Express the relations of the velocity and acceleration of a point belonging to a rigid body in rotational motion.
Velocity relation
If a rigid body is performing a rotational motion around a fixed axis, we can know its velocity at any point of the body with respect to the center of rotation.
The instantaneous velocity of a point in rotational motion is described by the following relation:
Where:
v = Velocity of a point in rotational motion
ω = angular velocity vector of the body. The direction is along the axis of rotation, the module is in rad/s
r = position vector of the point with respect to the axis of rotation
Acceleration relation
The acceleration of a point in rotational motion has two components, the tangential acceleration and the centripetal acceleration.
Tangential acceleration
The tangential acceleration is tangent to the trajectory and is expressed by the following relation.
at = tangential acceleration due to the variation of ω (vector)
ω = time derivative of the angular velocity, also called angular acceleration.
r = position vector of the point with respect to the axis of rotation.
Centripetal acceleration
Centripetal acceleration is directed towards the center of rotation and is expressed by the following relation.
Where:
ac = centripetal acceleration
ω = angular velocity vector of the body. The direction is along the rotation axis, the module is in rad/s
r = position vector of the point with respect to the rotation axis
Conclusions
In applied mechanics we know that we are in the presence of a translational motion when all its points move with the same speed and in the same direction, while we are in the presence of a rotary motion when a body rotates around an axis.
Question
Did you know that the study of rotary motion has very ancient origins? Did you know that one of the first scholars was the Greek philosopher Aristotle (384–322 BC)?

[ITALIAN]
11-06-2025 - Esercizio - moto traslatorio e moto rotatorio [EN]-[IT]
Immagine generata con IA, Microsoft Copilot
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento citato in oggetto svolgendo degli esercizi.
Il contesto in cui operiamo è quello della Meccanica applicata
(code notes: MOD+10)
moto traslatorio e moto rotatorio
Esercizio 01
Si diano le definizioni di moto traslatorio e di moto rotatorio di un corpo rigido.
Innanzitutto possiamo dire con certezza che il concetto di moto traslatorio e moto rotatorio di un corpo rigido sono due concetti basilari per progettare sistemi meccanici.
Qui di seguito sono spiegati entrambi i moti:
Moto traslatorio
Viene definito moto traslatorio di un corpo rigido quando tutti i punti di un corpo rigido si muovono lungo traiettorie parallele tra loro. Usando altre parole possiamo dire che la distanza relativa tra i punti del corpo non cambia e l’orientamento del corpo rimane costante durante il moto.
Il corpo rigido può compiere traiettorie che sono definibili da rette oppure traiettorie che sono riconducibili a curve. Nel primo caso parliamo di traslazione rettilinea, nel secondo caso parliamo di traslazione curvilinea.
Possiamo schematizzare i due moti come segue:
Moto rettilineo (traslazione)
Moto circolare (rotazione)
Esercizio riguardo il moto circolare Uniforme
Abbiamo un corpo che si muove lungo una circonferenza di raggio r=2m con velocità costante. Il corpo compie un giro completo in T=4s.
Proviamo a capire:
-Qual è la velocità angolare ω?
-Qual è la velocità tangenziale v?
-Qual è l'accelerazione centripeta ac?
-Quanti giri compie in 1 minuto?
la velocità angolare ω?
la velocità tangenziale v
Qual è l'accelerazione centripeta ac
Quanti giri compie in 1 minuto
Esercizio 02
Esprimere le relazioni della velocità e dell’accelerazione di un punto appartenente a un corpo rigido in moto rotatorio.
Relazione della velocità
Se un corpo rigido sta compiendo un moto rotatorio attorno ad un asse fisso, possiamo conoscere la sua velocità in un punto qualsiasi del corpo rispetto al centro di rotazione.
La velocità istantanea di un punto in moto rotatorio è descritta dalla seguente relazione:
Dove:
v = Velocità di un punto in moto rotatorio
ω = vettore velocità angolare del corpo. La direzione è lungo l’asse di rotazione, il modulo è in rad/s
r = vettore posizione del punto rispetto all’asse di rotazione
Relazione dell’accelerazione
L’accelerazione di un punto in moto rotatorio ha due componenti, l’accelerazione tangenziale e l’accelerazione centripeta.
L’accelerazione tangenziale
L’accelerazione tangenziale è tangente alla traiettoria ed è espressa dalla seguente relazione.
at = accelerazione tangenziale dovuta alla variazione di ω (vettoriale)
ω = derivata temporale della velocità angolare, detta anche accelerazione angolare.
r = vettore posizione del punto rispetto all’asse di rotazione.
L’accelerazione centripeta
L’accelerazione centripeta è diretta verso il centro di rotazione ed è espressa dalla seguente relazione.
Dove:
ac = accelerazione centripeta
ω = vettore velocità angolare del corpo. La direzione è lungo l’asse di rotazione, il modulo è in rad/s
r = vettore posizione del punto rispetto all’asse di rotazione
Conclusioni
In meccanica applicata sappiamo che siamo in presenza di un moto traslatorio quando tutti i suoi punti si muovono con la stessa velocità e nella stessa direzione, mentre siamo in presenza si un moto rotatorio quando un corpo ruota attorno a un asse.
Domanda
Lo sapevate che lo studio del moto rotatorio ha origini molto antiche? Lo sapevate che uno dei primi studiosi fu il filosofo greco Aristotele (384–322 a.C.)?
THE END


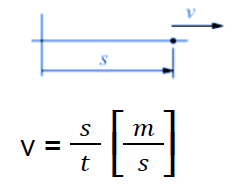
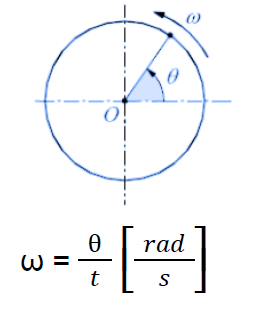
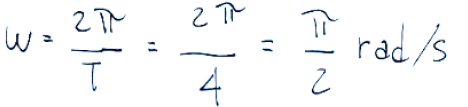
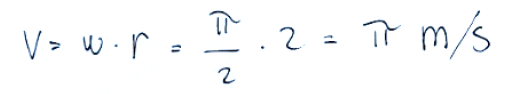

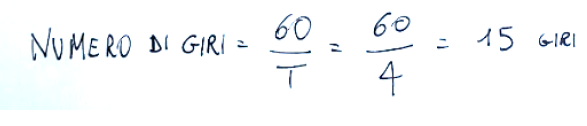
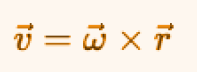
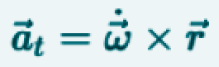
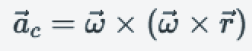
Upvoted! Thank you for supporting witness @jswit.