01-08-2025 - Education - Linear Programming Exercise [EN]-[IT]
Cover background image generated with AI, software used: copilot microsoft
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
[ENGLISH]
01-08-2025 - Education - Linear Programming Exercise [EN]-[IT]
Image generated with AI, Microsoft Copilot
With this post, I would like to provide some brief information on the topic mentioned above.
The context in which we operate is that of Operations Research
(code notes: MOD-79)
Linear Programming Exercise
Below, I will propose a simple linear programming exercise 01, often written as LP01.
A linear programming problem 01 consists of three main arguments:
01-Decision variables
02-Objective function
03-Constraints
Product production exercise
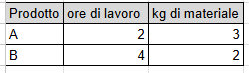
A company produces two products, called A and B.
Product A requires 2 hours of labor and 3 kg of material, while product B requires 4 hours of labor and 2 kg of material.
Below is a summary table.
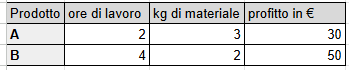
Then we know that this company has 100 hours of labor and 90 kg of material available.
Finally, we know that the sales department has estimated a profit of €30 for each unit of A and €50 for each unit of B.
Let's expand the table with the profits of products A and B.
Below is the table with the production constraints added (in yellow).
Problem Formulation
In this phase, we formulate the problem; that is, we collect the data and manage it so that we can then address this Linear Programming Problem 01
Decision Variables
Now let's identify the decision variables, that is, the variables we need to monitor to make the best decision.
We identify the decision variables as follows:
x1 = number of units of product A to be produced
x2 = number of units of product B to be produced
Objective Function
The objective function will be as follows:
MAX Z = 30x1 + 50x2
Where:
Z is the value of the objective function, that is, what we want to maximize.
30x1 + 50x2 is a linear combination of the decision variables with the respective coefficients 30 and 50.
X1 and X2 represent the number of units to be produced.
We can translate this function as follows:
[MAX Z = 30x1+50x2] = [Z = 30(units of A)+50(units of B)]
Constraints
Working hours: 2x1+3x2 ≤ 100h
Kg of material: 3x1+2x2 ≤ 90kg
Non-negativity constraint: x1≥0, x2≥0
Development with the simplex method
The simplex method models the problem as a system of linear equations with an objective function to be optimized (maximized or minimized).
We transform the problem into canonical form by taking the data for working hours and kg of available material. We introduce the waste variables to the equations.
We will therefore have:
In standard form, it is configured as follows:
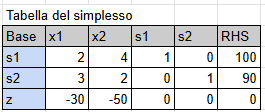
We can now construct the table of Simplex
Choosing the Entering Variable
We choose the entering variable based on the lowest coefficient.
The most negative coefficient in the Z row is -50, so the entering variable is x2.
Choice of the leaving variable
For this choice, the ratio of RHS/coefficient of x2 is calculated.
We call row 1 the row of s1 and row 2 the row of s2.
The minimum will be equal to 25, so s1 exits.
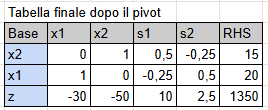
Pivot
Now we pivot on the x2 column in row 1. The new row one will be divided by 4.
And here is our table with the optimal solution. inside
Conclusions
The optimal solution for this exercise will be x1 = 20, x2 = 15, and maximum profit z = 1350
Question
Have you ever heard of linear programming? Did you know that these calculations are performed in companies structured to minimize costs or maximize profits?

[ITALIAN]
01-08-2025 - Education - Esercizio di programmazione lineare[EN]-[IT]
Immagine generata con IA, Microsoft Copilot
Con questo post vorrei fornire alcune brevi nozioni a riguardo dell’argomento citato in oggetto.
Il contesto in cui operiamo è quello della Ricerca Operativa
(code notes: MOD-79)
Esercizio di programmazione lineare
Qui di seguito proporrò un semplice esercizio di programmazione lineare 01, scritto spesso come PL01.
Un problema di programmazione lineare 01 si compone di tre argomenti principali:
01-Variabili decisionali
02-Funzione obiettivo
03-Vincoli
Esercizio di produzione prodotti
Un azienda produce due prodotti che chiamiamo A e B.
Il prodotto A richiede 2 ore di lavoro e 3 kg di materiale, mentre il prodotto B richiede 4 ore di lavoro e 2 kg di materiale
Qui di seguito una tabella riassuntiva
Poi sappiamo che questa azienda ha a disposizione 100 ore di lavoro e 90kg di materiale.
Come ultima cosa, sappiamo che l'ufficio commerciale ha stimato un profitto di 30 € per ogni unità A e di 50€ per ogni unità B
Ampliamo la tabella con i profitti dei prodotti A e B
Qui di seguito la tabella con l'aggiunta dei vincoli di produzione (in giallo)
Formulazione del problema
In questa fase formuliamo il problema, cioè raccogliamo i dati e le gestiamo in maniera che possiamo poi affrontare questo problema di programmazione lineare 01
Variabili decisionali
ora identifichiamo le variabili decisionali, cioè le variabili che dobbiamo monitorare per prendere la decisione migliore.
Le variabili decisionali le identifichiamo come segue.
x1=numero di unità di prodotto A da produrre
x2=numero di unità di prodotto B da produrre
Funzione Obiettivo
La funzione obiettivo sarà la seguente
MAX Z = 30x1+50x2
Dove:
Z è il valore della funzione obiettivo, cioè ciò che vogliamo massimizzare.
30x1+50x2 è una combinazione lineare delle variabili decisionali con i rispettivi coefficienti 30 e 50.
X1 e X2 rappresentano il numero di unità da produrre.
Possiamo tradurre questa funzione come segue:
[MAX Z = 30x1+50x2] = [Z = 30(unità di A)+50(unità di B)]
Vincoli
Ore di lavoro: 2x1+3x2 ≤ 100h
Kg di materiale: 3x1+2x2 ≤ 90kg
Vincolo di Non negatività: x1≥0, x2≥0
Sviluppo con il metodo del simplesso
Il metodo del simplesso modella il problema come un sistema di equazioni lineari con una funzione obiettivo da ottimizzare (massimizzare o minimizzare).
Trasformiamo il problema in forma canonica prendendo i dati delle ore di lavoro e dei kg di materiale disponibile. Alle equazioni introduciamo le variabili di scarto.
Avremo quindi che:
In forma standard si configura nella seguente maniera:
Possiamo ora costruirci la tabella del simplesso
Scelta della variabile entrante
Scegliamo la variabile entrante in base al coefficiente più basso.
Il coefficiente più negativo nella riga di Z è -50, quindi la variabile entrante è x2
scelta della variabile uscente
Per questa scelta viene calcolato il rapporto RHS/coefficiente di x2
Chiamano riga 1 la riga si s1 e riga 2 la riga di s2
Il minimo sarà uguale a 25, quindi esce s1
Pivot
A questo punto effettuiamo il pivot sulla colonna x2 in riga 1. La nuova riga uno verrà divisa per 4.
Ed ecco qua la nostra tabella con la soluzione ottima all'interno
Conclusioni
La soluzione ottima per questo esercizio sarà, x1 =20, x2=15 e profitto massimo z = 1350
Domanda
Avete mai sentito parlare di programmazione lineare? Lo sapevate che questi calcoli sono quelli che vengono effettuati in aziende strutturate per minimizzare i costi o massimizzare i profitti di un'azienda?
THE END


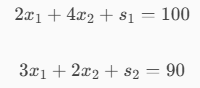
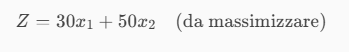
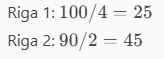
ottima spiegazione caro stefano , questi calcoli sono estremamente complessi a parer mio ma come li analizzi e spieghi te si ammorbidiscono molto come impatto per comprenderli al meglio !
sarebbe carino vedere anche vederli applicati con qualche esempio pratico cosi da comprendere ancora meglio la loro praticitá d uso
Grazie per il suggerimento... voglio provare a far degli articoli a riguardo della programmazione lineare e vedere se riesco a trovare un metodo per spiegarla benino.
Mai lavorato per un'azienda, quindi no (sempre e quando non si possa considerare azienda il laboratorio di Economia per il quale lavoravo negli anni di prima laurea, ma si trattava di ambito universitario pubblico, dove le rogne stavano nei tagli selvaggi all'università e ricerca, altro che calcolare profitti, ragione per cui ci pagavano una miseria).
Grazie per la risposta. Questi metodi vengono applicati proprio per non fare tagli selvaggi.. in maniera da tagliare solo dove è strettamente necessario. La programmazione lineare, fatta come si deve, aiuta sia a massimizzare che a minimizzare.
Upvoted! Thank you for supporting witness @jswit.
This post has been upvoted by @italygame witness curation trail
If you like our work and want to support us, please consider to approve our witness
Come and visit Italy Community