How does Steem's virtual supply behave when STEEM is priced above the haircut threshold?

Background

One of the things that has fascinated me with Steemonomics for a number of years is the counterintuitive way that Steem's virtual_supply behaves when the price of STEEM is above the haircut threshold. Specifically, when the price of STEEM goes up, the virtual_supply shrinks (and vice versa).

This happens because (equation 1):

virtual_supply = steem_supply + ( sbd_supply * steem_per_sbd ).

When the price of STEEM goes up, the number of steem_per_sbd goes down, and that reduces the second term of the equation.

This doesn't happen below the haircut threshold because the number of steem_per_sbd is held constant by the blockchain's haircut rule.

This increase (or decrease) has a downstream effect on the daily number of STEEM that are produced. So, it turns out that the best way to increase scarcity - setting aside "increase demand" - may be to increase the STEEM price, at least under certain conditions.

So, when the STEEM price is above the haircut threshold, even though the blockchain's core inflation rate will be positive, we can still see long periods of deflation. In practice, I think a single quarter is roughly the longest time period of deflation that I remember - or maybe one year.

We recently learned a surprising lesson about the behavior of Steem's virtual_supply when the STEEM price is below the haircut threshold. Specifically, SBD Conversions don't destroy debt. Instead, they lower the haircut price. And the downstream effects of lowering the haircut price are an increase to the virtual_supply and a corresponding increase in daily STEEM production.

So, I thought I'd start looking to see if we're in for any other surprises if/when the STEEM price crosses above the haircut threshold and stays there (currently about $0.156).

TL;DR - No big surprises so far. It looks like there might be a rule of thumb that 80% of virtual_supply reduction can be achieved when the price of STEEM is about 6 times the haircut threshold.

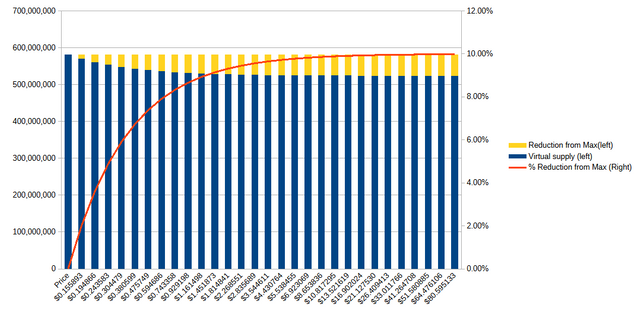
STEEM and SBD Supplies at current values

Typical for me, I started this exploration with a spread sheet, a table and a graph. Here's the behavior I found for virtual_supply at a variety of prices when holding the current_supply and current_sbd_supply constant (523905835.714 and 9074780.845, respectively).

Observations about the virtual supply:

1. The virtual supply is highest when the STEEM price is at or below the haircut threshold.
2. About 80% of the possible reduction can be realized by raising the STEEM price to about $0.93.
3. The maximum reduction possibility is 10% off from the max.
4. The haircut price is $0.156.

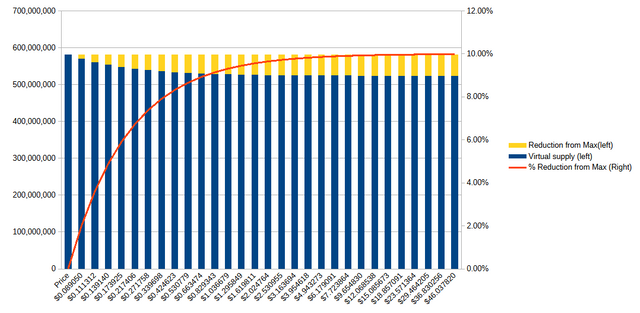
STEEM Supply at today's value, SBD Value based on the SPS wallet.

Let's suppose that it were somehow possible to burn all of the SBDs outside of the SPS ($5,183,743.585). How would that effect the virtual_supply behavior for STEEM prices above the haircut threshold? Here's what that looks like:

Observations about the virtual supply

1. The maximum is still at the haircut price (no surprise)
2. 80% of potential reductions can be achieved at about $0.53
3. The maximum reduction is still 10% of the minimum.
4. The haircut price would be $0.089.

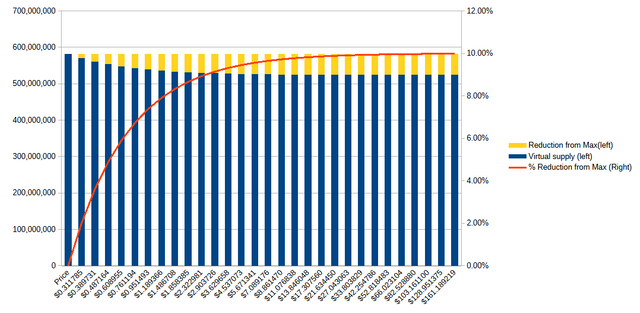
What if the number of SBDs is doubled?

Instead of reducing the SBD supply, what if we double it (18,149,562)? Here's what that looks like:

Observations about virtual supply

1. The max is still the max.
2. 80% of max reductions can now be achieved at about $1.85.
3. The max reduction is still 10% below the maximum virtual_supply.
4. The haircut price is about $0.312

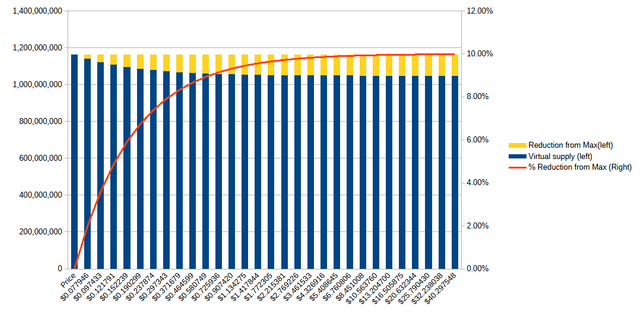
What if we double the STEEM supply?

So, now let's go back to the actual current_sbd_supply and double the current_supply of STEEM (1,047,811,671.428). Here's what that looks like:

Observations about virtual supply

1. The max virtual supply also doubled.
2. The max reduction is still 10%, but it's 10% of a much bigger number.
3. The haircut price would be $0.078
4. The 80% of possible reduction threshold would be around $0.46.

Summary

I don't think we need to do another one by halving the current supply to get a cursory understanding of what's going on here.

Obviously, these visuals will be different for any possible pairing of current_supply and current_sbd_supply, but the overall shape should always be similar. When we're on the left side of the curve, the effects of price changes are strong. On the right side of the curve, the effects are weak.

As a rule of thumb, the threshold where 80% of potential reductions have been accomplished seems to sit at roughly 6 times the haircut price. (it's actually a little below 6, maybe around 5 ²/₃ or 5 ³/₄, but it looks like 6 from the 10,000 foot level ;-).)

STEEM Supply	SBD Supply	Min Virtual Supply	Max Virtual Supply	80% Threshold	Haircut price
523,905,835.714	9,074,780.845	523905835.714	582,117,595	$0.93	$0.156
523,905,835.714	5,183,743.585	523905835.714	582,117,595	$0.53	$0.089
523,905,835.714	18,149,562	523905835.714	582,117,595	$1.85	$0.312
1,047,811,671.428	19,074,780.845	1,047,811,671.428	1,164,235,190	$0.46	$0.078

And we can summarize, directionally, how changes to current_supply and current_sbd_supply drive the haircut threshold, the 80% threshold, and the virtual_supply (assuming no other changes).

Parameter	Direction	haircut threshold	80% threshold	virtual supply
STEEM supply	up	down	down	up
STEEM supply	down	up	up	down
SBD supply	up	up	up	up (until the haircut threshold is reached)
SBD supply	down	down	down	down (when above the haircut threshold)

One last point, and perhaps its obvious, but the reason that the minimum value for the virtual_supply is always 10% below the maximum, and it always matches the current_supply is that as the STEEM price gets higher the number of steem_per_sbd goes towards zero. In turn, that drives the 2^nd term of the equation 1 towards 0, too.

Update:

In that last table, there may be(?) interesting implications for SBD conversions. Converting from SBD to STEEM involves reducing the SBD supply and increasing the STEEM supply. The first reduces the virtual_supply and the second increases it. I would have presumed those changes would offset each other. However, it's interesting to note that both changes tend to push the haircut price and the 80% threshold in the same direction (down), so maybe not(?)...

End update

---

Thank you for your attention!